RECOGNIZING PATTERNS IN NOISY DATA USING TRAINABLE FUNCTIONAL

RECOGNIZING PATTERNS IN NOISY DATA USING TRAINABLE ‘FUNCTIONAL’ STATE Faisal Waris
OUTLINE Background and Motivation Pattern Recognition with Finite State Machines Defining ‘Functional’ State Machines (Fn. SM) Trainable Fn. SM for Pattern Recognition in Noisy Data Train Fn. SM with Evolutionary Computing Algorithm Cultural Algorithm Framework (time permitting)

BACKGROUND & MOTIVATION - 3 TRENDS Cadillac Gesture Pad Automotive Gesture Control BMW In-the-air Gestures Android Auto e on h rtp n a Sm ratio o g t Au Inte We ara ble Co m pu tin g
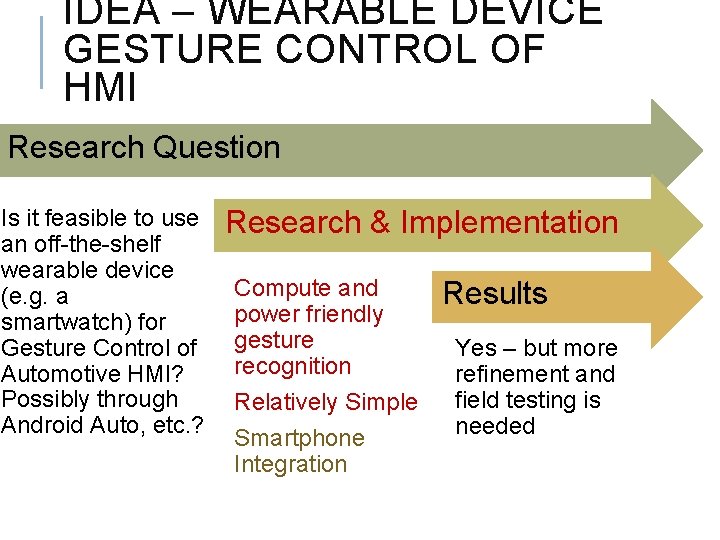
IDEA – WEARABLE DEVICE GESTURE CONTROL OF HMI Research Question Is it feasible to use an off-the-shelf wearable device (e. g. a smartwatch) for Gesture Control of Automotive HMI? Possibly through Android Auto, etc. ? Research & Implementation Compute and power friendly gesture recognition Relatively Simple Smartphone Integration Results Yes – but more refinement and field testing is needed
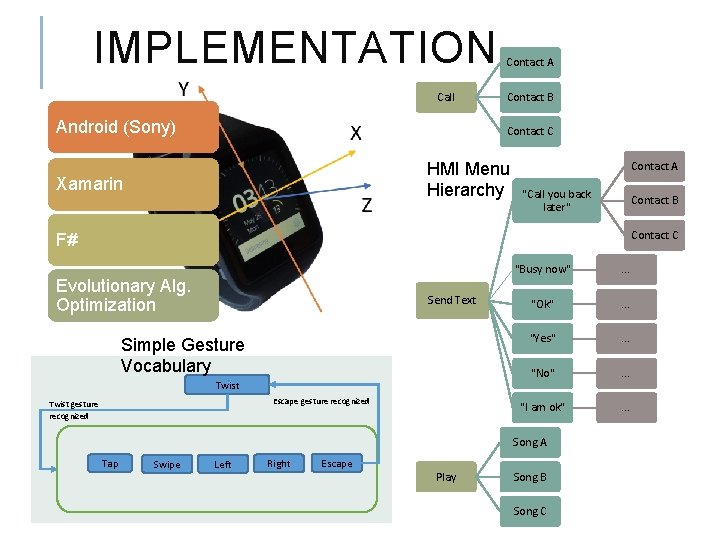
IMPLEMENTATION Call Android (Sony) Contact A Contact B Contact C HMI Menu Hierarchy Xamarin Contact A "Call you back later" Contact B Contact C F# Evolutionary Alg. Optimization Send Text Simple Gesture Vocabulary Twist Escape gesture recognized Twist gesture recognized "Busy now" . . . "Ok" . . . "Yes" . . . "No" . . . "I am ok" . . . Song A Tap Swipe Left Right Escape Play Song B Song C

GESTURE RECOGNITION ≈ PATTERN RECOGNITION IN NOISY (SEQUENTIAL) DATA Sensors Inherent Noise Fusion: Accelerometer, Gyro, Magnetometer Limb Moveme nt Not precise Vehicle Motion Acceleration Variations Cornering Bumps
SEQUENTIAL DATA, PATTERN RECOGNITION TECHNIQUES Hidden Markov Models Finite State Machines Time-Delay or Recurrent Neural Nets … Dynamic Time Warping Kernelbased Methods

FINITE STATE MACHINES (FSM) Plus • Computationally efficient • Suited for low power devices • Linear in the size of input • Simple & well-understood Minus • State-space explosion • Under some conditions • Can’t handle ‘probabilistic’ patterns by default

OUTLINE Background and Motivation Pattern Recognition with Finite State Machines Defining ‘Functional’ State Machines (Fn. SM) Trainable Fn. SM for Pattern Recognition in Noisy Data Train Fn. SM with Evolutionary Computing Algorithm

PATTERN RECOGNITION WITH FSM to recognize “…aaab…” pattern

OUTLINE Background and Motivation Pattern Recognition with Finite State Machines Defining ‘Functional’ State Machines (Fn. SM) Trainable Fn. SM for Pattern Recognition in Noisy Data Train Fn. SM with Evolutionary Computing Algorithm
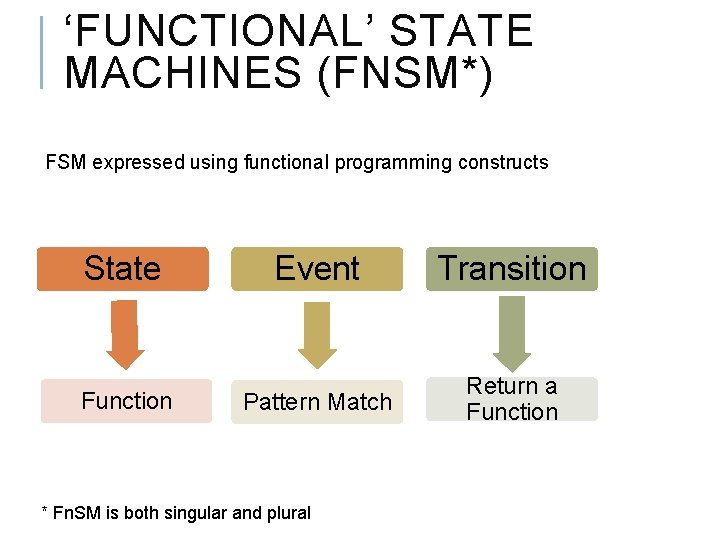
‘FUNCTIONAL’ STATE MACHINES (FNSM*) FSM expressed using functional programming constructs State Function Event Transition Pattern Match Return a Function * Fn. SM is both singular and plural

NATURAL TRANSFORMATION TO F# (ML) type M<'s> = M of ('s -> M<'s>) | 'a' -> M a 1 | _ -> M start and a 1 = function | 'a' -> M a 2 and a 2 = function | 'a' -> M a 3 and a 3 = function | 'b' -> M ``end`` and ``end`` _ = M ``end`` Fn. SM for recognizing the “aaab” pattern let rec start = function

STATE-SPACE EXPLOSION How about 3 ‘a’s and 3 ‘b’s in any order? Are 6 states enough? Need exponential # of states to recognize this pattern

FNSM FOR 3 ‘A’S AND 3 ‘B’S IN ANY ORDER let rec | 'a' | 'b' | _ f. Start = function -> f. AB 1 0 |> M -> f. AB 0 1 |> M -> f. Start |> M 1 0 and f. AB count. A count. B = function | 'a' when count. A + 1 = 3 -> f. B count. B |> | 'a' -> f. AB (count. A + 1) count. B |> | 'b' when count. B + 1 = 3 -> f. A count. A |> | 'b' -> f. AB count. A (count. B + 1) |> | _ -> failwith "invalid input" M M Partial Application to handle complex patterns (compress statespace) and f. A count = function | 'a' when count + 1 = 3 -> f. End |> M | 'a' -> f. A (count + 1) |> M | _ -> failwith "invalid input" and f. B count = function | 'b' when count + 1 = 3 -> f. End |> M | 'b' -> f. B (count + 1) |> M | _ -> failwith "invalid input" and f. End _ = printf "done"; f. End |> M

FNSM FOR WEARABLE DEVICE SENSOR DATA type Snsr. Event = { Snsr : Sensor. Type. Enum Ticks : long X : float; Y : float; Z Given an event data structure of this type (record). . . : float} We can define Fn. SM with Pattern Matching code like this let rec start = function | {Snsr=Linear. Acceleration; Z=z} … | {Snsr=Gyroscope; Z=z; X=x} … | {Snsr=s; Ticks=t} when … … Matches an event where the sensor is Linear Acceleration and binds the Z-Axis value to the variable ‘z’
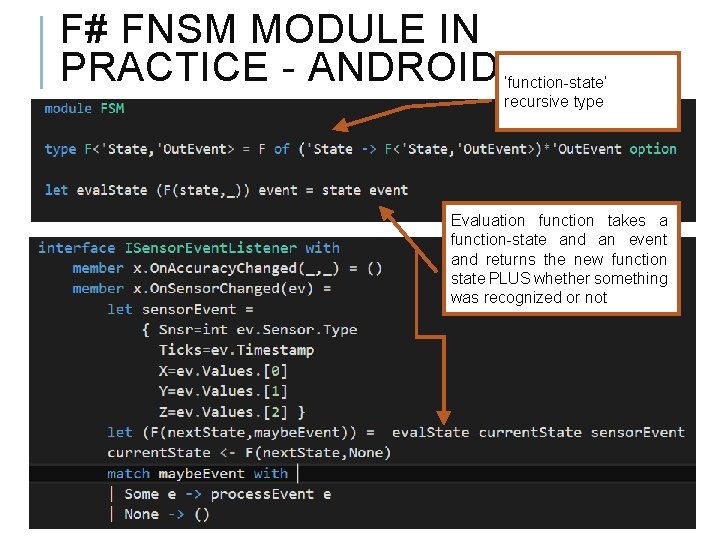
F# FNSM MODULE IN PRACTICE - ANDROID ‘function-state’ recursive type Evaluation function takes a function-state and an event and returns the new function state PLUS whether something was recognized or not

OUTLINE Background and Motivation Pattern Recognition with Finite State Machines Defining ‘Functional’ State Machines (Fn. SM) Trainable Fn. SM for Pattern Recognition in Noisy Data Train Fn. SM with Evolutionary Computing Algorithm Cultural Algorithm Framework

HANDLING NOISY DATA let rec start = function | {Snsr=Linear. Acceleration; Z=z} when abs z > 5. 0 // m/sec 2 possible_swing z 1 |> M | _ start |> M Partial Application + aggregation fo and possible_swing prev_z count = function probabilistic patterns | {Snsr=Linear. Acceleration; Z=z} when count < 30 let new_z = update. Avg (prev_z, count, z) possible_swing new_z (count + 1) |> M |{Snsr=Linear. Acceleration; Z=z} -> when <avg z greater some threshold> -> … Compute avg. linear acceleration over some count number of events

PARAMETERIZE FNSM FOR TRAINABILITY Fn. SM parameterized with configuration data let rec start cfg = function | {Snsr=Linear. Acceleration; Z=z} when abs z > cfg. MIN_Z_THRESHOLD possible_swing cfg z 1 | _ start Optimal configuration values can be through and possible_swing cfg prev_z count = function determined machine learning | {Snsr=Linear. Acceleration; Z=z} when count < cfg. COUNT_LIMIT let curr_z = update. Avg (prev_z, count, z) possible_swing cfg curr_z (count + 1) | … Partial Application + parameterization for trainability

FNSM – OTHER Fn. SM as partially applied values in other Fn. SM Hierarchical organization of state machines Call-return semantics / modularization Parallel execution of multiple ‘child’ state machines E. g. recognize 1 of many gestures at the same time Reactive Extensions Operators Write more compact and/or efficient custom operators for Rx (used with Apache Storm topology) Future: Project Brillo – Android for Io. T

FNSM CONCEPTS – INTERIM SUMMARY Fn. SM is a tool for modeling Finite State Machines • State = Function • Event = Pattern Match • Transition = Return a Function Partial Application • • State-space compression (handle complex patterns) Aggregation to address probabilistic patterns Parameterization for trainability Higher level structure

OUTLINE Background and Motivation Pattern Recognition with Finite State Machines Defining ‘Functional’ State Machines (Fn. SM) Trainable Fn. SM for Pattern Recognition in Noisy Data Train Fn. SM with Evolutionary Computing Algorithm

FNSM TRAINING – PARAMETERS Sample z_accel_front_thrsld = 2. 74647951 f; configuration gstr_time_limit = 460464225 L; parameters z_accel_back_thrsld = -4. 25041485 f; x_accel_tolerance = 3. 22107768 f; z_accel_avg_front_thrsld = 2. 39706802 f; y_accel_tolerance = 2. 86686087 f; z_accel_avg_back_thrsld = -4. 60432911 f; ret_x_accel_tolerance = 2. 9499104 f; xy_accel_tolerance = 2. 69525146 f; ret_y_accel_tolerance = 3. 1444633 f; avg_over_count = 1. 0 f; xz_rot_tolerance = 2. 97020698 f; gstr_time_limit = 781282632 L; y_rot_tolerance = 0. 526834428 f; xz_rot_tolerance = 2. 24759841 f; low_z_accel_limit = 3. 09724712 f y_rot_tolerance = 3. 57676268 f;

FNSM TRAINING – PROCESS 1 Labelled training data: Perform each gesture X times and record sensor output 2 Analyze gesture data and define parameterized Fn. SM for each gesture with initial (best guess) parameter values 3 4 Run the evolutionary computing optimization algorithm (EA) – given the: 1) Training data 2) Parameterized gesture Fn. SM 3) Optimization formulation To search for parameter values that yield the best value of the objective function Formulate a suitable optimization problem (fitness function) that uses the Fn. SM parameter values – this is key

FNSM TRAINING – OPTIMIZATION FORMULATION p = parm array values from a population individual g ∈ G ={Left, Right, Tap, Swipe}, the action gestures fit(p, g) = GC(g) – | count(p, g) – count. Not (p, g) | is the fitness function for a single gesture. This function’s value is calculated by running the Fn. SM parameterized with p over the training set for g. (The Ideal score is 0 when all of the 10 gesture instances are recognized and none any other gestures are recognized). Step (before / after Fitness CA) Score (max 120) Best guess -1. 5 parameter values W 1 and W 2 are weighting factors to control the influence of some of the terms. After CA 92. 5 In summary the fitness function is construed so that a perfect score of 120 is achieved when all 10 instances of a gesture type are recognized with the corresponding training set and none of any other type are optimization recognized, for each of the action gesture types. GC(g) = the # of gestures of type g in the training set for g (constant 10 for all gestures). count(p, g) = count of gesture of type g recognized when the p parameterized Fn. SM is run over the training set for g. (Ideal value is 10). count. Not(p, g) = count of all gestures of type [G – {g}] recognized when the p parameterized Fn. SM is run over the training set for g. (Ideal value is zero). count. D(p) = total count of any gesture in G recognized in the negative (driving) training set with a p parameterized Fn. SM. Ideal score is zero. This term is to reduce inadvertent recognition of any gestures.

SUMMARY Functional programming provides a powerful means of modeling FSM State | Events | Transitions function | pattern match | return a function Partial function application Model complex patterns (state-space compression) Handle probabilistic patterns through aggregation Make Fn. SM amenable to training or machine learning through parameterization Training: Training data + Optimization + EA Human modelled, machine optimized, computationally efficient pattern recognition Upcoming paper in IEEE Conference Swarm / Human Blended Workshop “Human-Defined, Machine-Optimized - Gesture Recognition using a mixed Approach” SHBI 2015 (Cleveland, Sept. 28, 29)

OUTLINE Background and Motivation Pattern Recognition with Finite State Machines Defining ‘Functional’ State Machines (Fn. SM) Trainable Fn. SM for Pattern Recognition in Noisy Data Train Fn. SM with Evolutionary Computing Algorithm Cultural Algorithm Framework

A TAXONOMY OF EVOLUTIONARY COMPUTING ALGORITHMS Genetic Algorithm Genetic Programming Biological Evolutionary Algorithm Evolutionary Computing Neural Net Artificial Immune System Ant Colony Optimization Social Particle Swarm Optimization Artificial Bee Colony Cultural Algorithm Hybrid algorithms + almost endless variations Molecular Chemical Reaction Optimization Simulated Annealing

“NO FREE LUNCH” THEOREM* Essentially states that if a search based algorithm is better on some problems, it will be worse on other problems (as compared to other search based algorithms) Explains the existence of the sheer variety of evolutionary computing algorithms Different search strategies are needed to tackle different problems * Wolpert & Macready (1997)

CULTURAL ALGORITHM FRAMEWORK* INSPIRED BY THE PROBLEM SOLVING ABILITIES OF CULTURE Belief Space accept() Knowledge Distributio n influence() Knowledge Sources Historical/Topological/Domain/Normative/Situatio nal Population Space *see Wikipedia page for introduction and further references

CULTURAL ALGORITHM TYPES– F# (ALMOST) type CA = { Population : Population Network : Network Knowlege. Distribution : Knowledge. Distribution Belief. Space : Belief. Space Acceptance. Function : Acceptance Influence. Function : Influence Update. Function : Update Fitness : Fitness } where: Topology = the network topology type of the population e. g. square, ring, global, etc. Knowledge = Situational | Historical | Normative | Topographical | Domain Individual = {Id: Id; Parms: Parm array; Fitness: float; KS: Knowledge} Id = int Parm = numeric value such as int, float, long, etc. Population = Individual array Network = Population Id Individual array Fitness = Parm array float Belief. Space = Knowledge. Source Tree Acceptance = Belief. Space Population Individual array Influence = Belief. Space Population Update = Belief. Space Individual array Belief. Space Knowledge. Distribution = Population Network Population Knowledge. Source = { Type : Knowledge Accept : Individual array * Knowledge. Source Influence : Individual }

THANK YOU contact: fwaris / wayne. edu
- Slides: 33