Recognition Template Matching o Chamfer Matching Statistical Pattern

Recognition ØTemplate Matching o Chamfer Matching ØStatistical Pattern Recognition (SPR) ØRobust object recognition using a cascade of Haar classifiers (Haar) ØPerformance Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 1

Template Matching - Topics § Applications § Matching criteria § Use of Fourier space § Use of chamfering § Control strategies Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 2

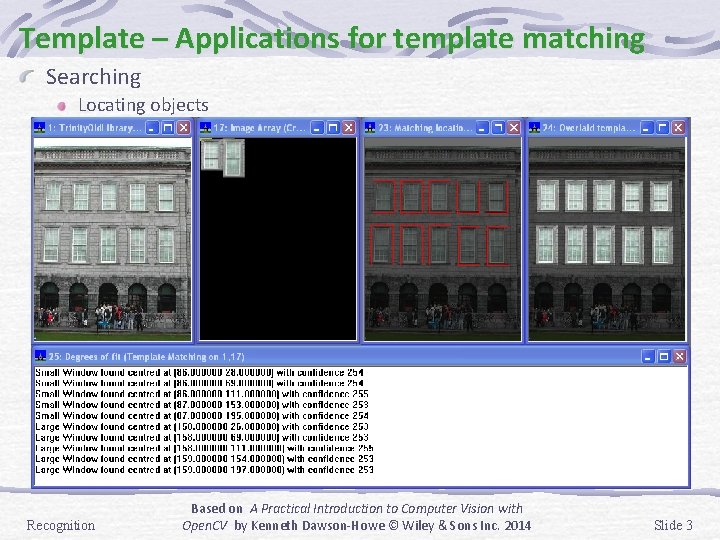
Template – Applications for template matching Searching Locating objects Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 3

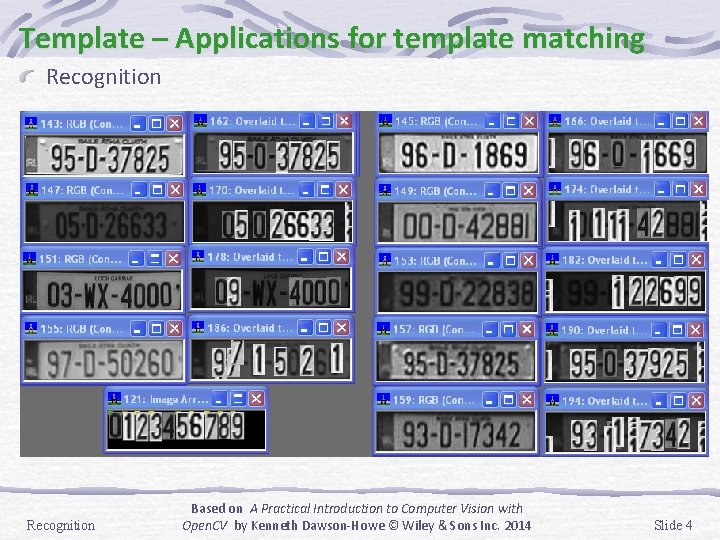
Template – Applications for template matching Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 4

Template – Applications for template matching Visual inspection Golden template matching Matching Stereo Vision Tracking Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 5

Template – Matching Algorithm Basic Algorithm Inputs – Image & Object For every possible position of the object in the image Evaluate a match criterion Search for local maxima of the match criterion above some threshold Problems ‘Every possible position’? ‘Match criterion’ ‘Local maxima above some threshold’ Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 6

Template – Matching criteria Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 7

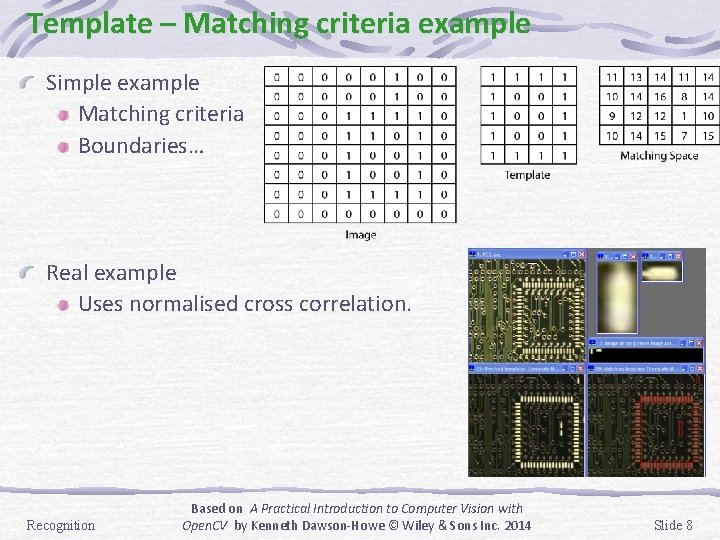
Template – Matching criteria example Simple example Matching criteria Boundaries… Real example Uses normalised cross correlation. Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 8

Template Matching in Open. CV Mat matching_space; matching_space. create( search_image. cols–template_image. cols+1, search_image. rows–template_image. rows+1, CV_32 FC 1 ); match. Template( search_image, template_image, matching_space, CV_TM_CCORR_NORMED ); // Other measures: CV_TM_CCORR, CV_TM_SQDIFF, // CV_TM_SQDIFF_NORMED Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 9

Template – Finding Local Maxima in Open. CV Local maxima – Dilate + Look for unchanged values + Threshold Local minima – Erode + Look for unchanged values + Threshold Mat dilated, thresholded_matching_space, local_maxima, thresholded_8 bit; dilate( matching_space, dilated, Mat()); compare( matching_space, dilated, local_maxima, CMP_EQ ); threshold( matching_space, thresholded_matching_space, threshold, 255, THRESH_BINARY ); thresholded_matching_space. convert. To( thresholded_8 bit, CV_8 U ); bitwise_and( local_maxima, thresholded_8 bit, local_maxima ); Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 10

Template – Control Strategies for Matching Goal: Localise close copies Size, orientation Geometric distortion Use an image hierarchy Low resolution first Limit higher resolution search Search higher probability locations first Known / learnt likelihood From lower resolution Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 11

Template – Chamfer matching Template matching requires very close matches Objects often appear very slightly different Orientation Noise Sampling We want a more flexible approach Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 12

Template – Chamfering Compute chamfered image for a binary edge image. For every point If (edge point) Set c(i, j) = 0 Else Set c(i, j) = ∞ For j = min to max For i = min to max c(i, j) = minq AL [distance( (i, j), q ) + f( q )] For j = max to min For i = max to min c(i, j) = minq BR [distance( (i, j), q ) + f( q )] Canny( gray_image, edge_image, 100, 200, 3); threshold(edge_image, 127, 255, THRESH_BINARY_INV); distance. Transform(edge_image, chamfer_image, CV_DIST_L 2, 3); Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 13

Template – Chamfer matching Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 14

Template – Chamfering for matching Compare with boundary template Sum of chamfer values for boundary points Low values best Chamfer matching is a simple routine to write (provided in the text); Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 15

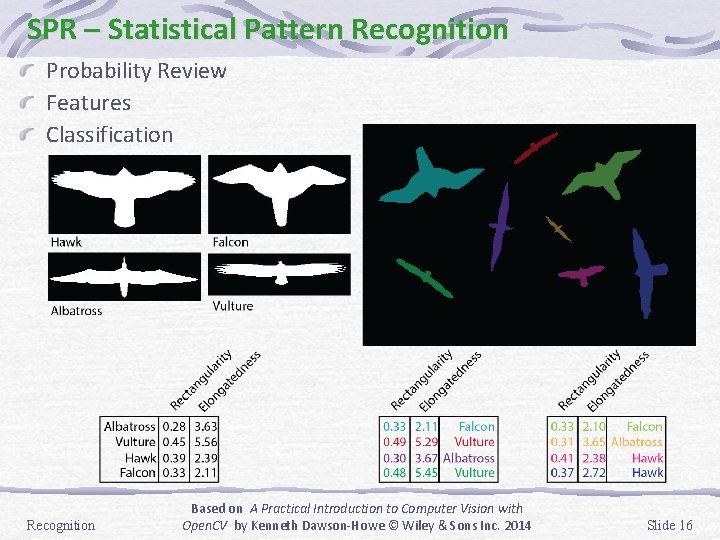
SPR – Statistical Pattern Recognition Probability Review Features Classification Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 16

SPR – Probabitity Review – Basics P(A) = limn N(A) / n Probability of two events A and B: Independent: P(AB) = P(A)P(B) Dependent: P(AB) = P(A|B)P(B) Conditional Probability P(A|B) Typical problem: Given some evidence x from an unknown object. What class Wi is the object? Training A-priori probability – p(x | Wi) Relative probability – p(Wi) A-posteriori probability – p(Wi | x) Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 17

SPR – Probabitity Review – Bayes Theorem For two classes A and B the a-posteriori probability is: P(B|A) = P(A|B)P(B) / P(A) Where Wi forms a partitioning of the event space: p(Wi | x) = Recognition _p(x | Wi)P(Wi)__ j p(x | Wj)P(Wj) Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 18

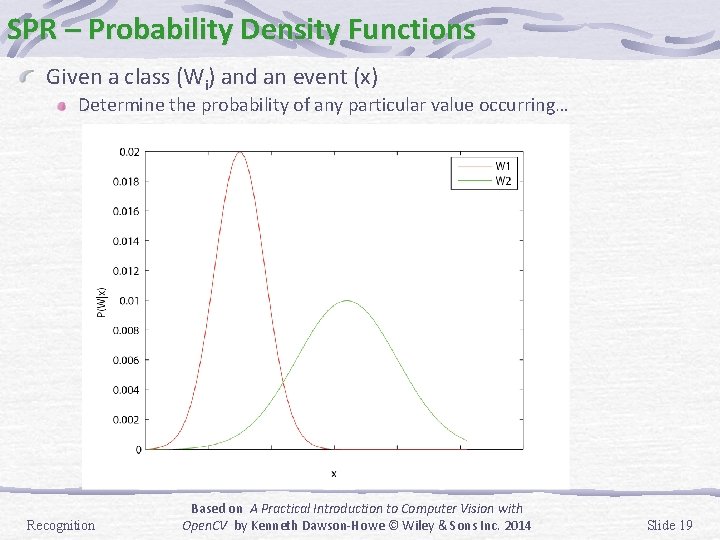
SPR – Probability Density Functions Given a class (Wi) and an event (x) Determine the probability of any particular value occurring… Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 19

SPR – Features: Area Count the points Location dependent? Determine from n polygon vertices vector<Point>> contours; vector<Vec 4 i> hierarchy; find. Contours( binary_image, contours, hierarchy, CV_RETR_TREE, CV_CHAIN_APPROX_NONE); for (int contour=0; (contour>=0); contour=hierarchy[contour][0]) { double area = contour. Area(contours[contour]) + contours[contour]. size()/2 + 1; for (int hole=hierarchy[contour][2]; (hole>=0); hole=hierarchy[hole][0]) area -= ( contour. Area(contours[hole]) – contours[hole]. size()/2 + 1 ); } Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 20

SPR – Features: Elongatedness CANNOT BE the ratio of the length and width of the minimum bounding rectangle Ratio of region area divided by the square of it’s thickness Erosion Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 21

SPR – Features: Minimum Bounding Rectangle Turn rectangle through discrete steps Only one quadrant Metrics: Length to Width ratio Length / Width Rectangularity Area / (Length * Width) Convex Hull to Minimum Bounding Rectangle area ratio Area inside convex hull / (Length * Width) Rotated. Rect min_bounding_rectangle = min. Area. Rect(contours[contour_number]); Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 22

SPR – Features: Convex hull Smallest convex region Algorithm 1. 2. 3. 4. Start with Any point on convex hull Previous vector direction Search all other boundary points Find point with least angle to previous vector Switch to new point and vector Go to 2 unless new point = start point. Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 23

SPR – Features: Convex hull vector<Point>> hulls(contours. size()); for (int contour=0; (contour<contours. size()); contour++) { convex. Hull(contours[contour], hulls[contour]); } Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 24

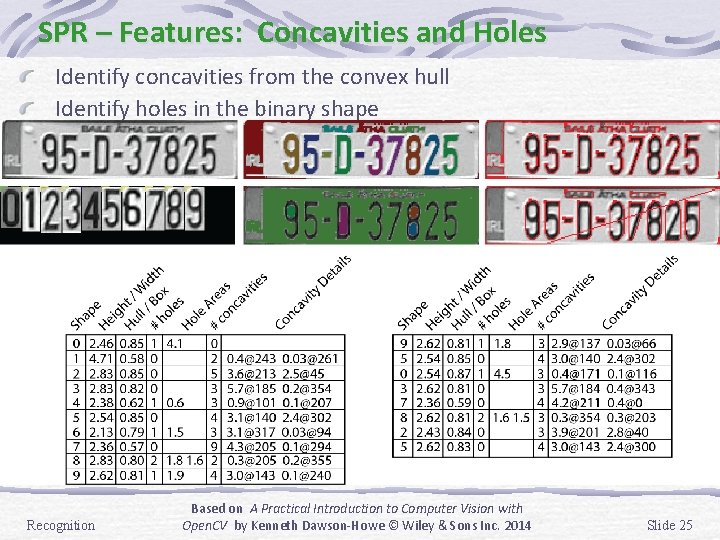
SPR – Features: Concavities and Holes Identify concavities from the convex hull Identify holes in the binary shape Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 25

SPR – Features: Concavities and Holes vector<int>> hull_indices(contours. size()); vector<Vec 4 i>> convexity_defects(contours. size()); for (int contour=0; (contour<contours. size()); contour++) { convex. Hull( contours[contour], hull_indices[contour] ); convexity. Defects( contours[contour], hull_indices[contour], convexity_defects[contour]); } Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 26

SPR – Features: Perimeter Length and Circularity Perimeter length Approximately the number of boundary elements contours[contour]. size() Should really take into account direction Circularity = Perimeter length / (4*π*Area) Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 27

SPR – Features: Moments & Moment invariants Moments measure the distribution of shape Central moments: Scale invariant moments: Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 28

SPR – Features: Moment invariants / Hu moments: Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 29

SPR – Features: Moments and Moment invariants Moments contour_moments; double hu_moments[7]; contour_moments = moments( contours[contour] ); Hu. Moments( contour_moments, hu_moments ); Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 30

SPR – Classification – Introduction Object recognition Classes (w 1, w 2, … w. R) Classifier Input Pattern / features (x 1, x 2, … xn) Feature space Choosing the features (Example) Clusters in feature space Separability Hyper-surfaces Linear separability Inseperable classes Classifiers Minimum Distance Classifier Linear Classifier Probabilistic Classifier Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 31

SPR – Minimum distance classifier Each class represented by an exemplar For an unknown object Determine the distance to the exemplars Pick the class with the smallest distance Unknown class? Distance must be less than some threshold Advantages Training Computational Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 32

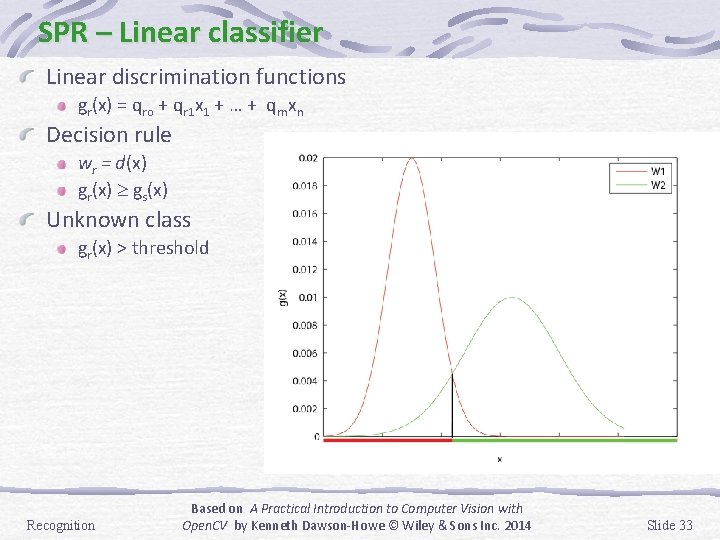
SPR – Linear classifier Linear discrimination functions gr(x) = qro + qr 1 x 1 + … + qrnxn Decision rule wr = d(x) gr(x) gs(x) Unknown class gr(x) > threshold Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 33

SPR – Probabilistic classifier Optimal classifier Based on Probability Density Functions Remove normalisation from Bayes rule… Resultant Discrimination function: Mean Loss Function: Advantages / Disadvantages Accuracy Extensive training Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 34

SPR – Classifier learning Training set Must be representative Must be inductive Training set size Training set provides the unknown statistical information Size will typically have to be increased several times Sample learning strategies Supervised: Probability density estimation – estimating p(x|wr) & P(wr) Training set includes class specification for every instance Unsupervised: Cluster Analysis Look for similarities in feature space Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 35

SPR: Real example Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 36

Haar – Robust Object Detection using a cascade of classifiers. Features Efficient calculation Training Weak & Strong Classifiers Adaboost Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 37

Haar – In Open. CV. Cascade. Classifier cascade; if( !cascade. load( "haarcascades/haarcascade_frontalface_alt. xml" ) { vector<Rect> faces; equalize. Hist( gray_image, gray_image ); cascade. detect. Multi. Scale( gray_image, faces, 1. 1, 2, CV_HAAR_SCALE_IMAGE, Size(30, 30) ); } Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 38

Haar – Overview Training using a number of positive and negative samples Uses simple (Haar like) features Efficient calculation… Selects a large number of these features during training to create strong classifiers Links a number of strong classifiers into a cascade for recognition Efficiency… Can work at different scales Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 39

Haar – Features determined as the difference of the sums of a number of rectangular regions Place the mask in a specific location and at a specific scale Then subtract the sum of the ‘white pixels’ from the sum of the ‘black pixels’ Why does this work? Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 40

Haar – Efficient Calculation – Integral Image: Every point ii(i, j) = i’=0. . i j’=0. . j image(i’, j’) Sum of points in rectangle D: sum(D) = ii(p) + ii(s) – ii(q) – ii(r) Features can be computed at any scale for the same cost An integral function is provided which computes the integral image both normally and at 45 o Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 41

Haar – Training Number of possible features. the variety of feature types allowed variations in size and position Training must Identify the best features to use at each stage To do this positive and negative samples are needed… Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 42

Haar – Weak & Strong Classifiers Weak Classifier pjfeaturej(x) < pjθj Tune threshold (θj) Strong Classifiers Combine a number of weak classifiers… E. g. 100% true positives with only 40% false positives using only two face features… Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 43

Haar – Strong Classifiers – Adaboost Given n example images x 1. . xn together with classifications y 1. . yn where yi = 0, 1 for negative and positive examples respectively. Initialise weights w 1, i = 1 / (2*(m*(1 - yi)+l*yi)) where m and l are the number of negative and positive examples respectively. For t=1, …, T 1. Normalize the weights (i. e. for all i): wt, i = wt, i / ( j=1. . n wt, j) 2. For each feature, j, train a weak classifier hj(x) and evaluate the error taking into account the weights: j = i wt, i | hj(xi) – yi | 3. Select the classifier, hj(x), with the lowest j , save as ct(x) with error Et 4. Update the weights (i. e. for all i): wt+1, i = wt, i t(1 - ei ) where ei = | ct(xi) – yi | and t = Et / (1–Et) The final strong classifier is: h(x)= 1 if t=1. . T αtct(x) ½ t=1. . T αt , 0 otherwise where αt = log 1/ t Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 44

Haar – Classifier cascade Object recognition is possible with a single strong classifier To improve detection rates AND to reduce computation time: A cascade of strong classifiers can be used Each stage either accepts or rejects Only those accepted pass to the next stage Efficient computation… Strong classifiers trained using Ada. Boost On the remaining set of data Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 45

Haar – Recognition Face recognition 38 stages 6000+ features 4916 positive samples 9544 negative samples Scale independence Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 46

Performance Two aspects Computation time double before_tick_count=static_cast<double>(get. Tick. Count()); // Put methods to be timed here… double after_tick_count=static_cast<double>(get. Tick. Count()); double duration_in_ms=1000. 0*(after_tick_countbefore_tick_count) / get. Tick. Frequency(); Success and failure rates What is the correct answer? We need ground truth How do we assess success? We need metrics. Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 47

Performance – Ground Truth Has to be manually computed Very difficult to get agreement… Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 48

Performance – Metrics Compute TP TN FP FN and then compute… Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 49

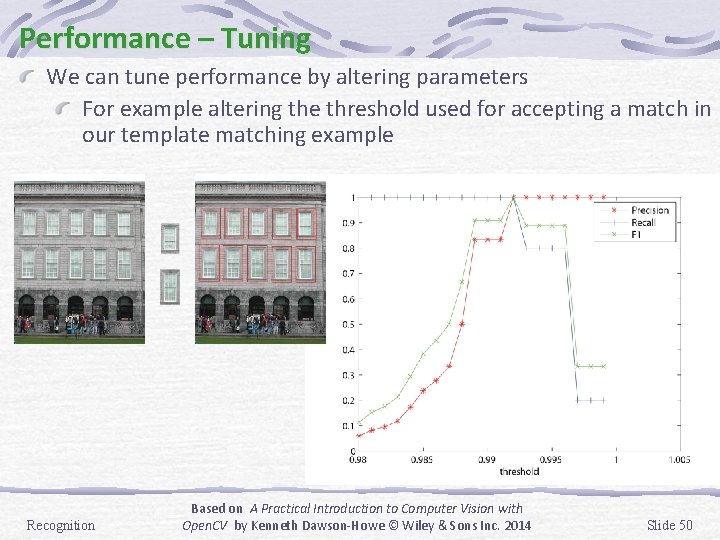
Performance – Tuning We can tune performance by altering parameters For example altering the threshold used for accepting a match in our template matching example Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 50

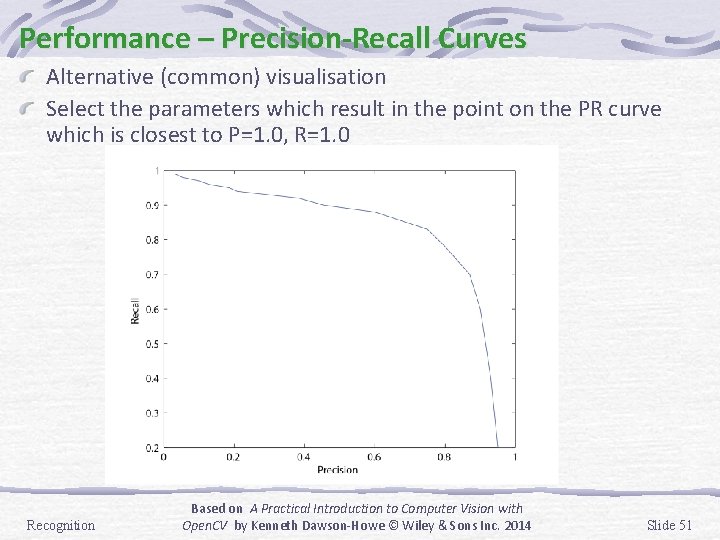
Performance – Precision-Recall Curves Alternative (common) visualisation Select the parameters which result in the point on the PR curve which is closest to P=1. 0, R=1. 0 Recognition Based on A Practical Introduction to Computer Vision with Open. CV by Kenneth Dawson-Howe © Wiley & Sons Inc. 2014 Slide 51