Recitation 1 Probability Review Parts of the slides

Recitation 1 Probability Review Parts of the slides are from previous years’ recitation and lecture notes

Basic Concepts l A sample space S is the set of all possible outcomes of a conceptual or physical, repeatable experiment. (S can be finite or infinite. ) l E. g. , S may be the set of all possible outcomes of a dice roll: l An event A is any subset of S. l Eg. , A= Event that the dice roll is < 3.

Probability l A probability P(A) is a function that maps an event A onto the interval [0, 1]. P(A) is also called the probability measure or probability mass of A. Worlds in which A is false Worlds in which A is true P(A) is the area of the oval

Kolmogorov Axioms l All probabilities are between 0 and 1 l 0 ≤ P(A) ≤ 1 l P(S) = 1 l P(Φ)=0 l The probability of a disjunction is given by l P(A U B) = P(A) + P(B) − P(A ∩ B) ¬A ∩ ¬B B A∩B? A

Random Variable l l A random variable is a function that associates a unique number with every outcome of an experiment. S Discrete r. v. : l l l The outcome of a dice-roll: D={1, 2, 3, 4, 5, 6} Binary event and indicator variable: l Seeing a “ 6" on a toss Þ X=1, o/w X=0. l This describes the true or false outcome a random event. Continuous r. v. : l The outcome of observing the measured location of an aircraft w X(w)

Probability distributions l l l For each value that r. v X can take, assign a number in [0, 1]. Suppose X takes values v 1, …vn. Then, l l P(X= v 1)+…+P(X= vn)= 1. Intuitively, the probability of X taking value vi is the frequency of getting outcome represented by vi

Discrete Distributions l Bernoulli distribution: Ber(p) l Binomial distribution: Bin(n, p) l Suppose a coin with head prob. p is tossed n times. l What is the probability of getting k heads? l How many ways can you get k heads in a sequence of k heads and n-k tails?

Continuous Prob. Distribution l A continuous random variable X is defined on a continuous sample space: an interval on the real line, a region in a high dimensional space, etc. l X usually corresponds to a real-valued measurements of some property, e. g. , length, position, … l It is meaningless to talk about the probability of the random variable assuming a particular value --- P(x) = 0 l Instead, we talk about the probability of the random variable assuming a value within a given interval, or half interval, etc. l l l
![Probability Density l If the prob. of x falling into [x, x+dx] is given Probability Density l If the prob. of x falling into [x, x+dx] is given](http://slidetodoc.com/presentation_image_h/c6a3dd14f57cdcaab1ddff3ac17f2273/image-9.jpg)
Probability Density l If the prob. of x falling into [x, x+dx] is given by p(x)dx for dx , then p(x) is called the probability density over x. l The probability of the random variable assuming a value within some given interval from x 1 to x 2 is equivalent to the area under the graph of the probability density function between x 1 and x 2. l Probability mass: Gaussian Distribution

Continuous Distributions l Uniform Density Function l Normal (Gaussian) Density Function l The distribution is symmetric, and is often illustrated as a bell-shaped curve. l l Two parameters, m (mean) and s (standard deviation), determine the location and shape of the distribution. The highest point on the normal curve is at the mean, which is also the median and mode.

Statistical Characterizations l Expectation: the centre of mass, mean, first moment): l l Sample mean: Variance: the spread: l Sample variance:

Conditional Probability l P(X|Y) = Fraction of worlds in which X is true given Y is true l H = "having a headache" l F = "coming down with Flu" l l P(H)=1/10 l P(F)=1/40 l P(H|F)=1/2 P(H|F) = fraction of headache given you have a flu = P(H∧F)/P(F) l Definition: Y X∧Y l Corollary: The Chain Rule X

The Bayes Rule l What we have just did leads to the following general expression: This is Bayes Rule
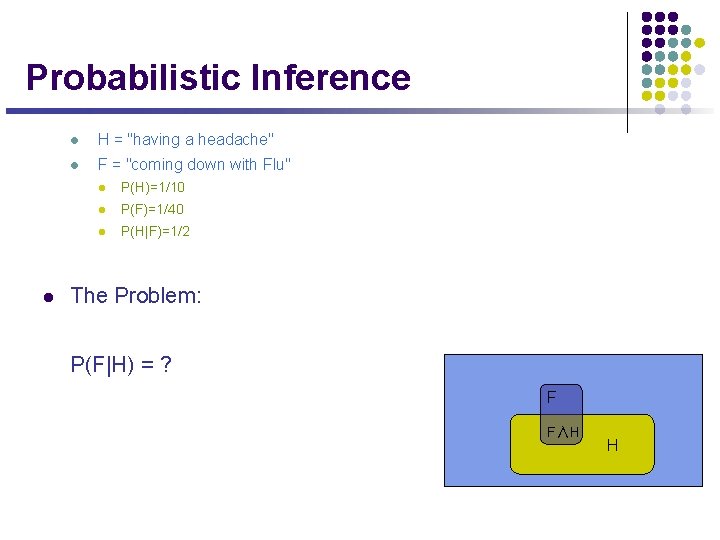
Probabilistic Inference l l H = "having a headache" l F = "coming down with Flu" l P(H)=1/10 l P(F)=1/40 l P(H|F)=1/2 The Problem: P(F|H) = ? F F∧H H

Joint Probability l A joint probability distribution for a set of RVs gives the probability of every atomic event (sample point) l l P(Flu, Drink. Beer) = a 2 × 2 matrix of values: B ¬B F 0. 005 0. 02 ¬F 0. 195 0. 78 Every question about a domain can be answered by the joint distribution, as we will see later.
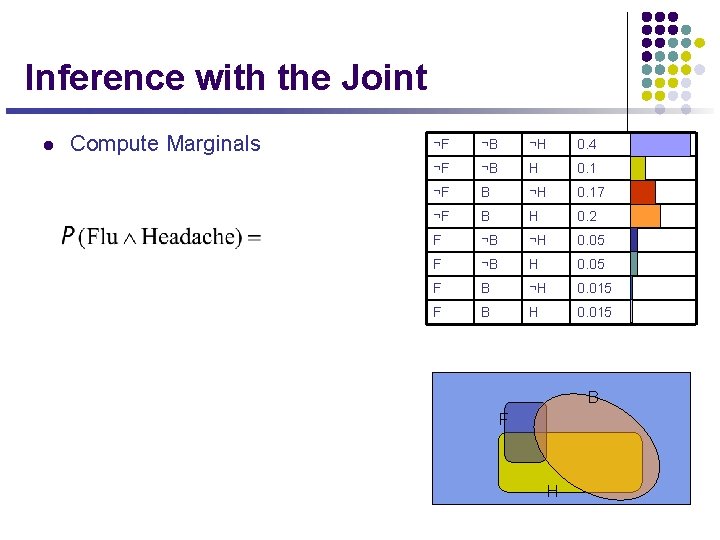
Inference with the Joint l Compute Marginals ¬F ¬B ¬H 0. 4 ¬F ¬B H 0. 1 ¬F B ¬H 0. 17 ¬F B H 0. 2 F ¬B ¬H 0. 05 F ¬B H 0. 05 F B ¬H 0. 015 F B H 0. 015 B F H
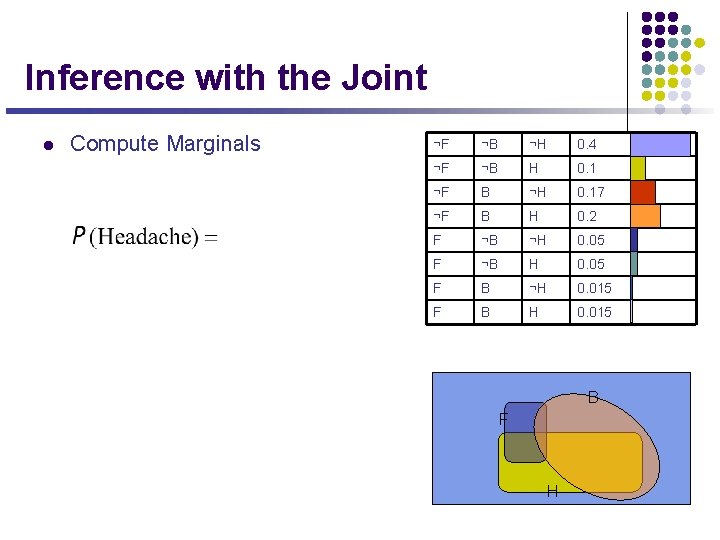
Inference with the Joint l Compute Marginals ¬F ¬B ¬H 0. 4 ¬F ¬B H 0. 1 ¬F B ¬H 0. 17 ¬F B H 0. 2 F ¬B ¬H 0. 05 F ¬B H 0. 05 F B ¬H 0. 015 F B H 0. 015 B F H

Inference with the Joint l Compute Conditionals ¬F ¬B ¬H 0. 4 ¬F ¬B H 0. 1 ¬F B ¬H 0. 17 ¬F B H 0. 2 F ¬B ¬H 0. 05 F ¬B H 0. 05 F B ¬H 0. 015 F B H 0. 015 B F H

Inference with the Joint l Compute Conditionals l ¬F ¬B ¬H 0. 4 ¬F ¬B H 0. 1 ¬F B ¬H 0. 17 ¬F B H 0. 2 F ¬B ¬H 0. 05 F ¬B H 0. 05 F B ¬H 0. 015 F B H 0. 015 General idea: compute distribution on query variable by fixing evidence variables and B F summing over hidden variables H

Conditional Independence l Random variables X and Y are said to be independent if: l l P(X ∩ Y) =P(X)*P(Y) Alternatively, this can be written as l P(X | Y) = P(X) and l P(Y | X) = P(Y) l Intuitively, this means that telling you that Y happened, does not make X more or less likely. l Note: This does not mean X and Y are disjoint!!! Y X∧Y X

Rules of Independence --- by examples l P(Virus | Drink. Beer) = P(Virus) iff Virus is independent of Drink. Beer l P(Flu | Virus; Drink. Beer) = P(Flu|Virus) iff Flu is independent of Drink. Beer, given Virus l P(Headache | Flu; Virus; Drink. Beer) = P(Headache|Flu; Drink. Beer) iff Headache is independent of Virus, given Flu and Drink. Beer

Marginal and Conditional Independence l Recall that for events E (i. e. X=x) and H (say, Y=y), the conditional probability of E given H, written as P(E|H), is P(E and H)/P(H) (= the probability of both E and H are true, given H is true) l E and H are (statistically) independent if P(E) = P(E|H) (i. e. , prob. E is true doesn't depend on whether H is true); or equivalently P(E and H)=P(E)P(H). l E and F are conditionally independent given H if P(E|H, F) = P(E|H) or equivalently P(E, F|H) = P(E|H)P(F|H)

x Why knowledge of Independence is useful l Lower complexity (time, space, search …) l Motivates efficient inference for all kinds of queries l Structured knowledge about the domain l easy to learning (both from expert and from data) l easy to grow

Density Estimation l A Density Estimator learns a mapping from a set of attributes to a Probability l Often know as parameter estimation if the distribution form is specified l l Binomial, Gaussian … Three important issues: l Nature of the data (iid, correlated, …) l Objective function (MLE, MAP, …) l Algorithm (simple algebra, gradient methods, EM, …) l Evaluation scheme (likelihood on test data, predictability, consistency, …)

Parameter Learning from iid data l Goal: estimate distribution parameters q from a dataset of N independent, identically distributed (iid), fully observed, training cases D = {x 1, . . . , x. N} l Maximum likelihood estimation (MLE) 1. One of the most common estimators 2. With iid and full-observability assumption, write L(q) as the likelihood of the data: 3. pick the setting of parameters most likely to have generated the data we saw:

Example 1: Bernoulli model l Data: l l We observed N iid coin tossing: D={1, 0, 1, …, 0} Representation: Binary r. v: l Model: l How to write the likelihood of a single observation xi ? l The likelihood of dataset. D={x 1, …, x. N}:

MLE l Objective function: l We need to maximize this w. r. t. q l Take derivatives wrt q or Frequency as sample mean

Overfitting l Recall that for Bernoulli Distribution, we have l What if we tossed too few times so that we saw zero head? We have and we will predict that the probability of seeing a head next is zero!!! l The rescue: l Where n' is know as the pseudo- (imaginary) count l But can we make this more formal?

Example 2: univariate normal l Data: l We observed N iid real samples: D={-0. 1, 10, 1, -5. 2, …, 3} l Model: l Log likelihood: l MLE: take derivative and set to zero:

The Bayesian Theory l The Bayesian Theory: (e. g. , for date D and model M) P(M|D) = P(D|M)P(M)/P(D) l l the posterior equals to the likelihood times the prior, up to a constant. This allows us to capture uncertainty about the model in a principled way

Hierarchical Bayesian Models l q are the parameters for the likelihood p(x|q) a are the parameters for the prior p(q|a). l We can have hyper-parameters, etc. l We stop when the choice of hyper-parameters makes no difference to the marginal likelihood; typically make hyperparameters constants. l Where do we get the prior? l l Intelligent guesses l Empirical Bayes (Type-II maximum likelihood) computing point estimates of a :

Bayesian estimation for Bernoulli l Beta distribution: l Posterior distribution of q : l Notice the isomorphism of the posterior to the prior, l such a prior is called a conjugate prior

Bayesian estimation for Bernoulli, con'd l Posterior distribution of q : l Maximum a posteriori (MAP) estimation: l Posterior mean estimation: l Prior strength: A=a+b l Bata parameters can be understood as pseudo-counts A can be interoperated as the size of an imaginary data set from which we obtain the pseudo-counts

Bayesian estimation for normal distribution l Normal Prior: l Joint probability: l Posterior: Sample mean
- Slides: 34