RECIPROCITY THEOREM ENGR VIKRAM KUMAR B E ELECTRONICS

RECIPROCITY THEOREM ENGR. VIKRAM KUMAR B. E (ELECTRONICS) M. E (ELECTRONICS SYSTEM ENGG: ) MUET JAMSHORO 1

_ The reciprocity theorem is applicable only to single-source networks and states the following: _ The current I in any branch of a network, due to a single voltage source E anywhere in the network, will equal the current through the branch in which the source was originally located if the source is placed in the branch in which the current I was originally measured. _ The location of the voltage source and the resulting current may be interchanged without a change in current 2

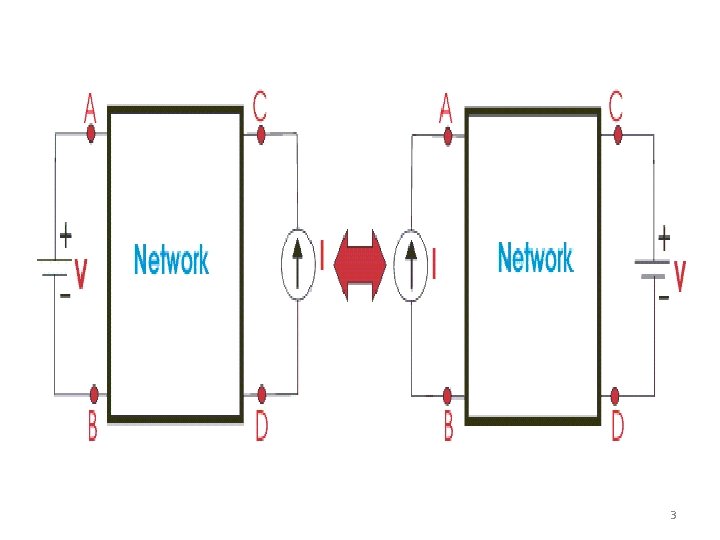
3

COMPENSATION THEOREM 4

q. This theorem based on one basic concept. Ø When electric current flows through any resistor, there would be a voltage drop across the resistor according to Ohm’s law. Ø This dropped voltage opposes the source voltage. Ø Voltage drop across an electric resistance in any network can be assumed as a voltage source acting opposite to the source voltage. 5

q According to this theorem; ● Any resistance in a network may be replaced by a voltage source that has zero internal resistance and a voltage equal to the voltage drop across the replace resistance due to the current which was flowing through it. ● This imaginary voltage source is directed opposite to the voltage source of that replaced resistance. 6

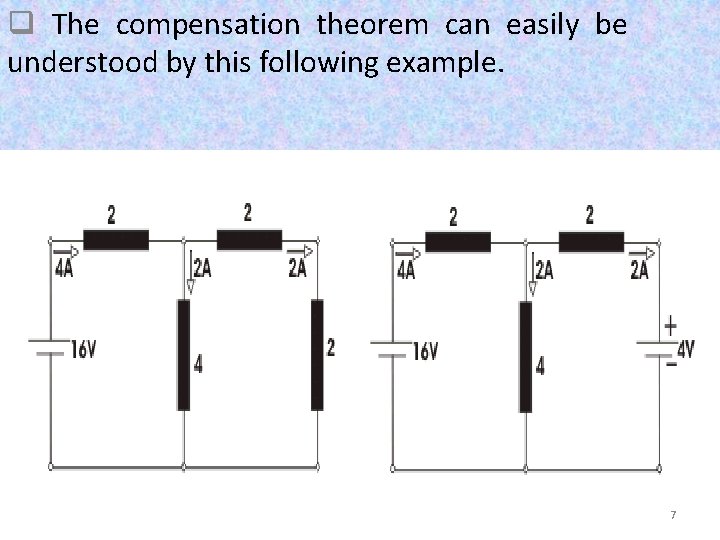
q The compensation theorem can easily be understood by this following example. 7

Ø This theorem is particularly useful for the following two purposes : (a) For analyzing those networks where the values of the branch elements are varied and for studying the effect of tolerance on such values. (b) For calculating the sensitivity of bridge network. 8

Ø As applied to d. c. circuits, it may be stated in the following to ways : (i) In its simplest form. this theorem asserts that any resistance ‘R’ in a branch of a network in which a current ‘I’ is flowing can be replaced, for the purposes of calculations, by a voltage equal to - IR. OR 9

(ii) If the resistance of any branch of network is changed from R to (R + ΔR) where the current flowing originally is I, the change of current at any other place in the network may be calculated by assuming that an e. m. f. - I. ΔR has been injected into the modified branch while all other sources have their e. m. f. s. suppressed and are represented by their internal resistances only. 10

THE END 11