Reciprocal functions secant cotangent Secant is the reciprocal





- Slides: 12

Reciprocal functions secant, cotangent Secant is the reciprocal of cosine. Reciprocal means to flip the ratio. Cosecant is the reciprocal of sine. Reciprocal means to flip the ratio. Cotangent is the reciprocal of tangent. Reciprocal means to flip the ratio.

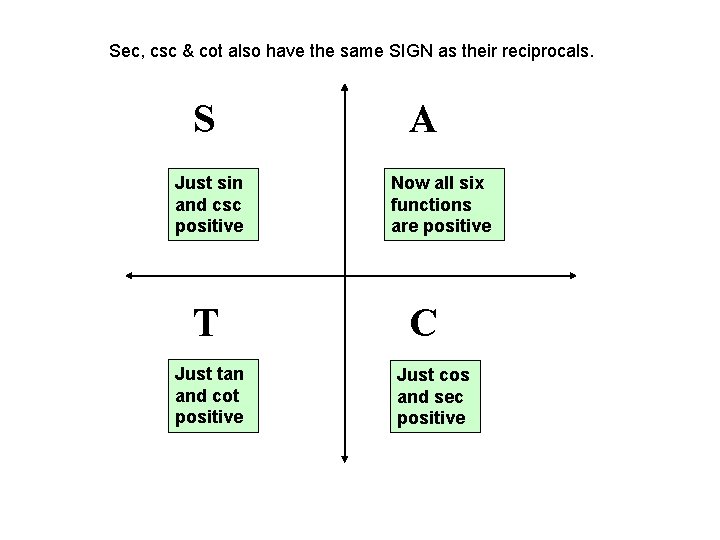
Sec, csc & cot also have the same SIGN as their reciprocals. S Just sin and csc positive T Just tan and cot positive A Now all six functions are positive C Just cos and sec positive

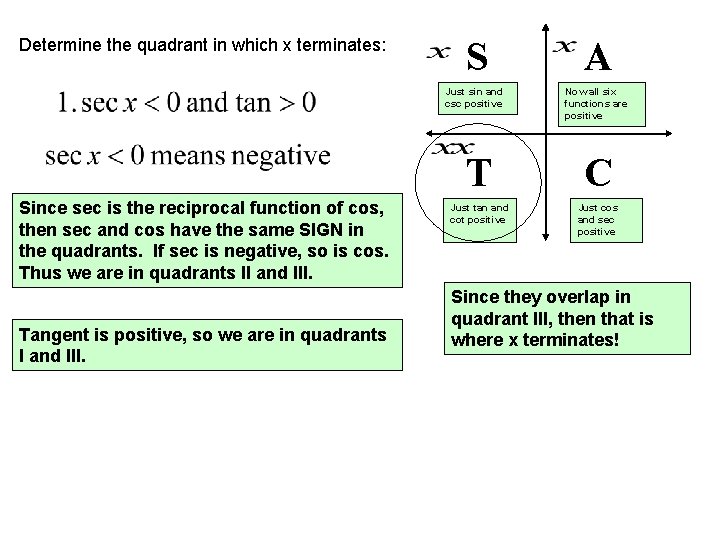
Determine the quadrant in which x terminates: Since sec is the reciprocal function of cos, then sec and cos have the same SIGN in the quadrants. If sec is negative, so is cos. Thus we are in quadrants II and III. Tangent is positive, so we are in quadrants I and III. S A Just sin and csc positive Now all six functions are positive T C Just tan and cot positive Just cos and sec positive Since they overlap in quadrant III, then that is where x terminates!

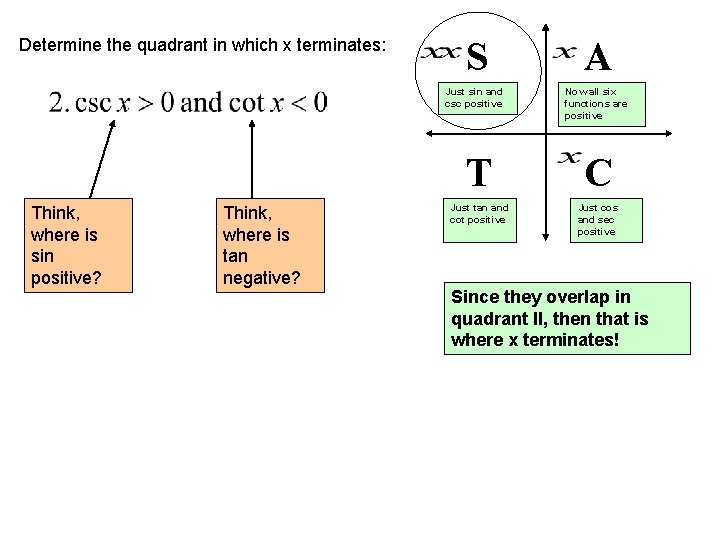
Determine the quadrant in which x terminates: Think, where is sin positive? Think, where is tan negative? S A Just sin and csc positive Now all six functions are positive T C Just tan and cot positive Just cos and sec positive Since they overlap in quadrant II, then that is where x terminates!

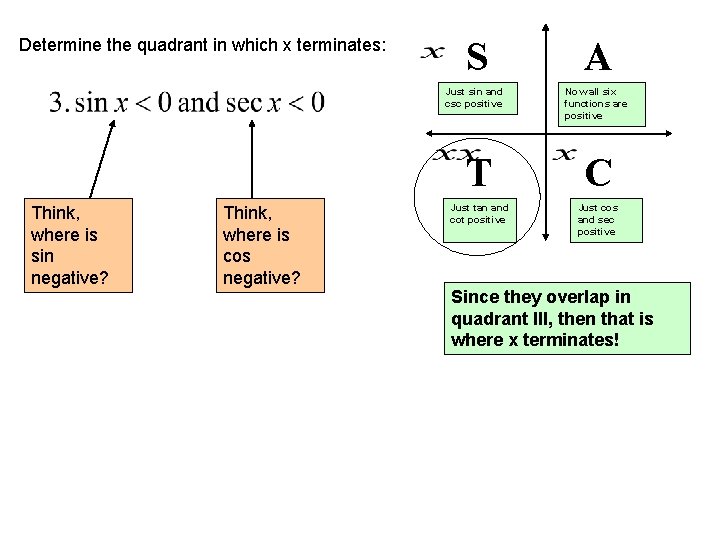
Determine the quadrant in which x terminates: Think, where is sin negative? Think, where is cos negative? S A Just sin and csc positive Now all six functions are positive T C Just tan and cot positive Just cos and sec positive Since they overlap in quadrant III, then that is where x terminates!

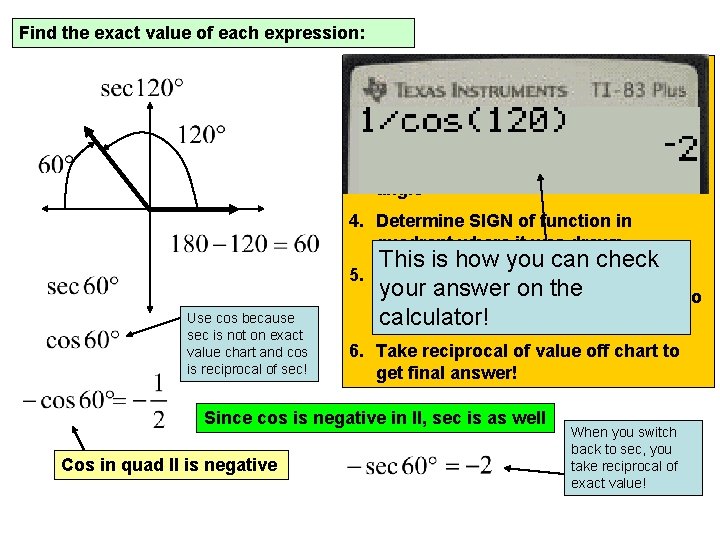
Find the exact value of each expression: Step: 1. Start by drawing the given angle 2. Find the reference angle 3. Rewrite the function using reference angle 4. Determine SIGN of function in quadrant where it was drawn 5. Use cos because sec is not on exact value chart and cos is reciprocal of sec! This is how you can check Now find exact value using exact your chart answer the function to value (use on reciprocal get value off chart) calculator! 6. Take reciprocal of value off chart to get final answer! Since cos is negative in II, sec is as well Cos in quad II is negative When you switch back to sec, you take reciprocal of exact value!

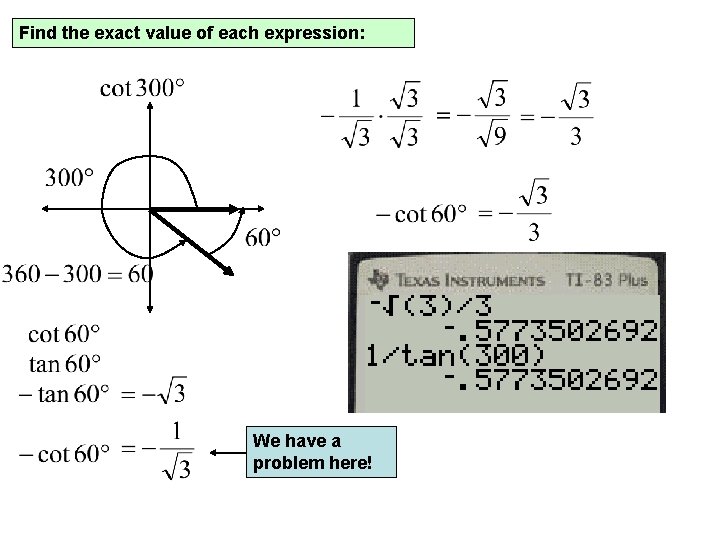
Find the exact value of each expression: We have a problem here!

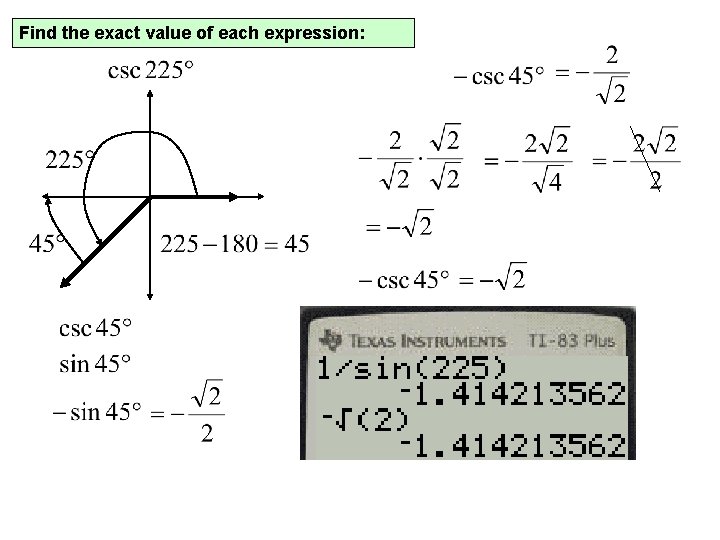
Find the exact value of each expression:

Page 10 Sec is the reciprocal of cos, so:

Page 10

Page 10

Page 10