Recent Applications of Linear Programming in Memory of

Recent Applications of Linear Programming in Memory of George Dantzig Yinyu Ye Department if Management Science and Engineering Stanford University ISMP 2006

Outline • LP in Auction Pricing – Parimutuel Call Auction • Proving Theorems using LP – Uncapacitated Facility Location – Core of Cooperative Game • Applications of LP Algorithms – – Walras-Arrow-Debreu Equilibrium Linear Conic Programming • Photo Album of George (Applications presented here are by no means complete)

Outline • LP in Auction Pricing – Parimutuel Call Auction • Proving Theorems using LP – Uncapacitated Facility Location – Core of Cooperative Game • Applications of LP Algorithms – Walras-Arrow-Debreu equilibrium – Linear Conic Programming • Photo Album of George

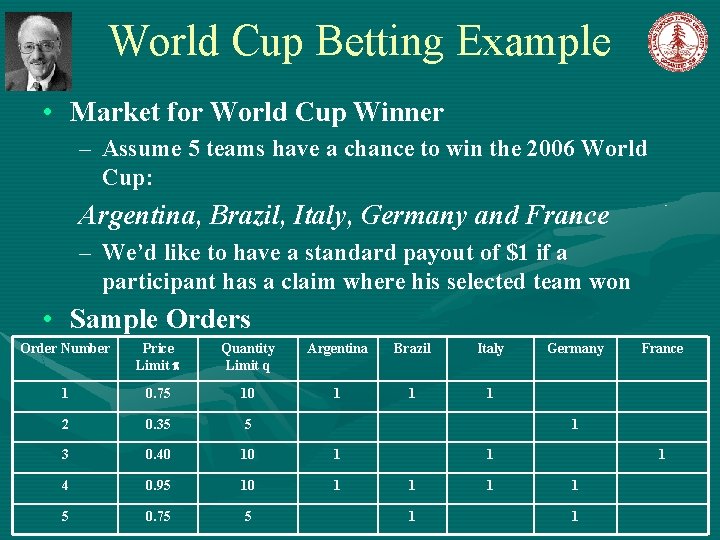
World Cup Betting Example • Market for World Cup Winner – Assume 5 teams have a chance to win the 2006 World Cup: Argentina, Brazil, Italy, Germany and France – We’d like to have a standard payout of $1 if a participant has a claim where his selected team won • Sample Orders Order Number Price Limit Quantity Limit q Argentina Brazil Italy 1 0. 75 10 1 1 1 2 0. 35 5 3 0. 40 10 1 4 0. 95 10 1 5 0. 75 5 Germany France 1 1 1 1

Markets for Contingent Claims • A Contingent Claim Market – S possible states of the world (one will be realized). – N participants who (say j), submit orders to a market organizer containing the following information: • ai, j - State bid (either 1 or 0) • qj – Limit contract quantity • πj – Limit price per contract – Call auction mechanism is used by one market organizer. – If orders are filled and correct state is realized, the organizer will pay the participant a fixed amount w for each winning contract. – The organizer would like to determine the following: • pi – State price • xj – Order fill

Central Organization of the Market • Belief-based • Central organizer will determine prices for each state based on his beliefs of their likelihood • This is similar to the manner in which fixed odds bookmakers operate in the betting world • Generally not self-funding • Parimutuel • A self-funding technique popular in horseracing betting

Parimutuel Methods • Definition – Etymology: French pari mutuel, literally, mutual stake A system of betting on races whereby the winners divide the total amount bet, after deducting management expenses, in proportion to the sums they have wagered individually. • Example: Parimutuel Horseracing Betting Bets Horse 1 Horse 2 Horse 3 Total Amount Bet = $6 Outcome: Horse 2 wins Two winners earn $2 per bet plus stake back: Winners have stake returned then divide the winnings among themselves

Parimutuel Market Microstructure Boosaerts et al. [2001], Lange and Economides [2001], Fortnow et al. [2003], Yang and Ng [2003], Peters et al. [2005], etc LP pricing for the contingent claim market

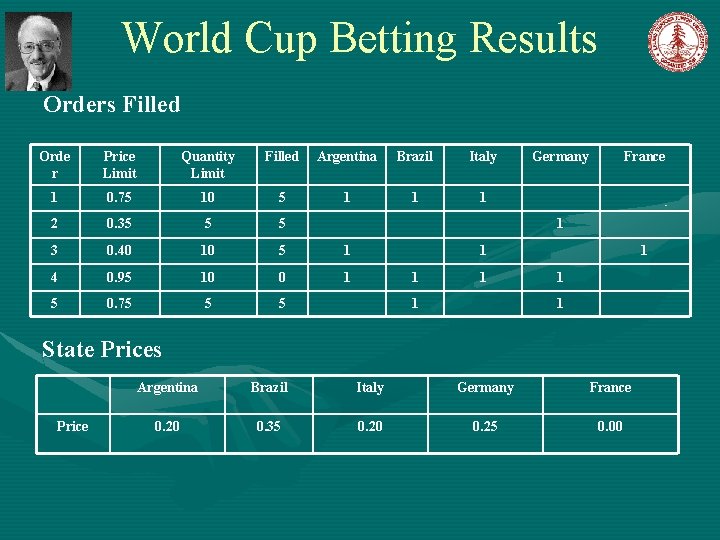
World Cup Betting Results Orders Filled Orde r Price Limit Quantity Limit Filled Argentina Brazil Italy 1 0. 75 10 5 1 1 1 2 0. 35 5 5 3 0. 40 10 5 1 4 0. 95 10 0 1 5 0. 75 5 5 Germany France 1 1 1 1 State Prices Price Argentina Brazil Italy Germany France 0. 20 0. 35 0. 20 0. 25 0. 00

Outline • LP in Auction Pricing – Parimutuel Call Auction • Proving Theorems using LP – Uncapacitated Facility Location – Core of Cooperative Game • Applications of LP Algorithms – Walras-Arrow-Debreu equilibrium – Linear Conic Programming • Photo Album of George

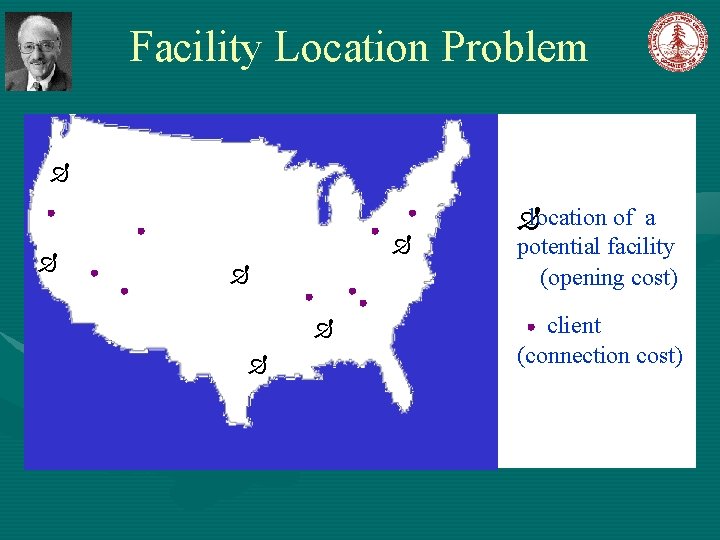
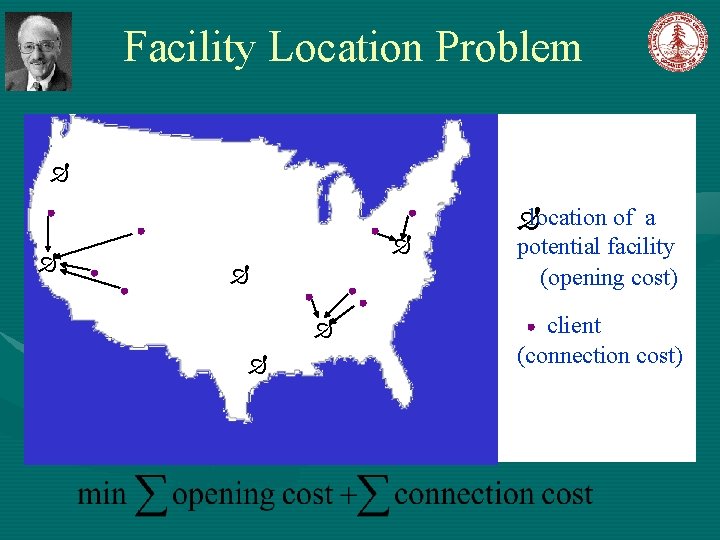
Facility Location Problem Input A set of clients or cities D • A set of facilities F with facility cost fi • Connection cost Cij, (obey triangle inequality) • Output • A subset of facilities F’ • An assignment of clients to facilities in F’ Objective • Minimize the total cost (facility + connection)

Facility Location Problem location of a potential facility (opening cost) client (connection cost)

Facility Location Problem location of a potential facility (opening cost) client (connection cost)

R-Approximate Solution and Algorithm

Hardness Results v. NP-hard. Cornuejols, Nemhauser & Wolsey [1990]. v 1. 463 polynomial approximation algorithm implies NP =P. Guha & Khuller [1998], Sviridenko [1998].

ILP Formulation • Each client should be assigned to one facility. • Clients can only be assigned to open facilities.

LP Relaxation and its Dual Interpretation: clients share the cost to open a facility, and pay the connection cost.

Bi-Factor Dual Fitting A bi-factor (Rf, Rc)-approximate algorithm is a max(Rf, Rc)-approximate algorithm

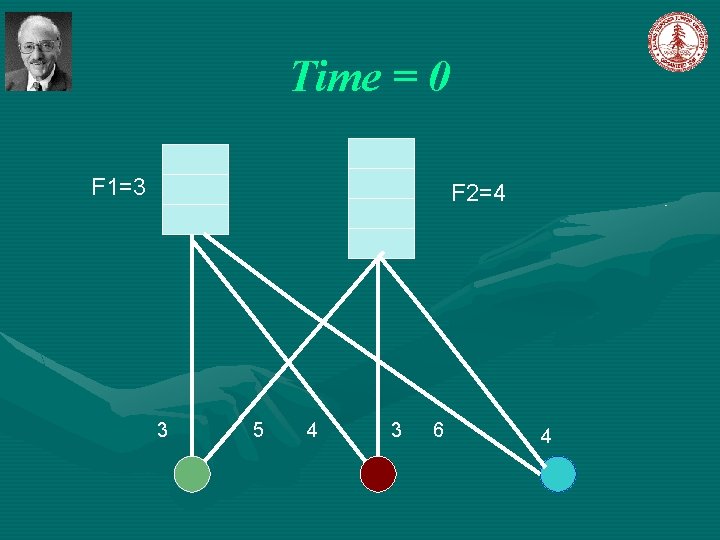
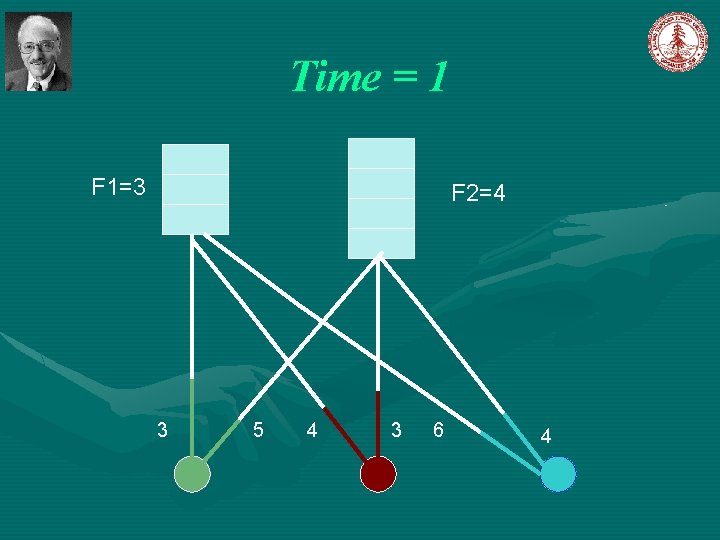
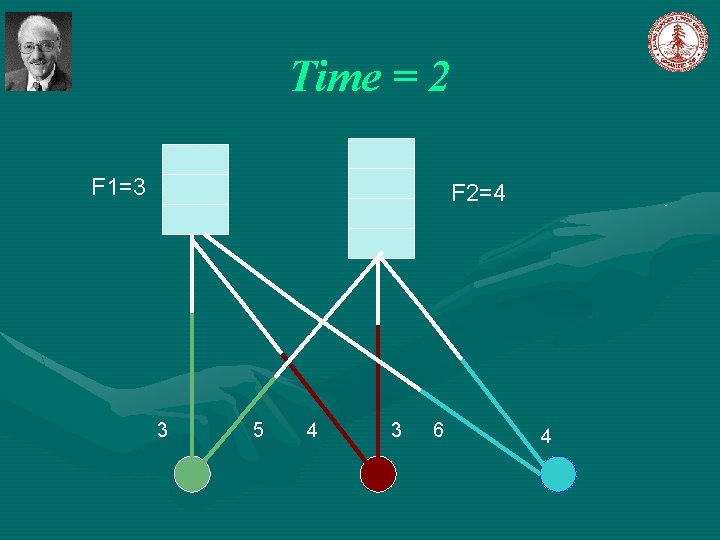
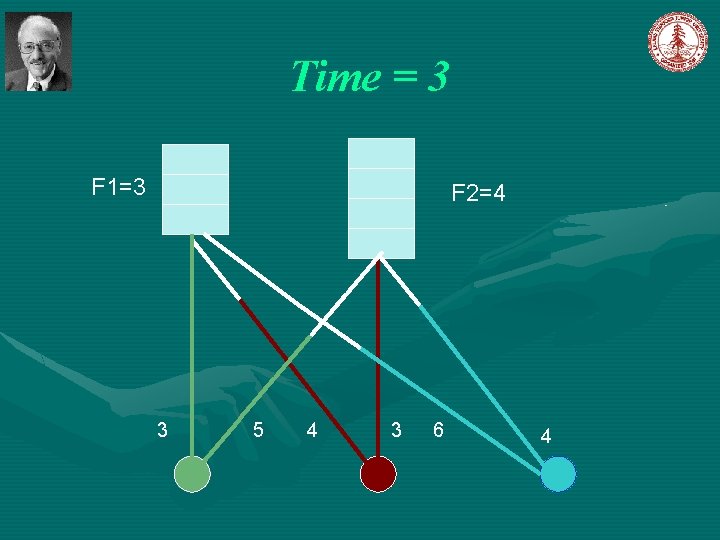
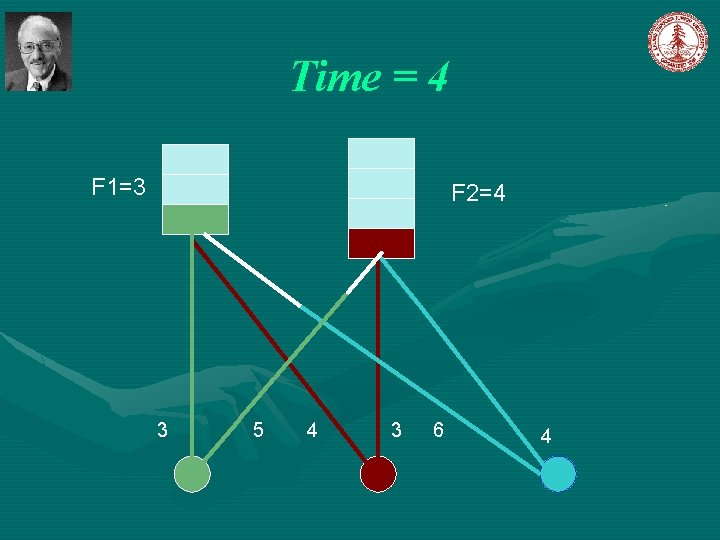
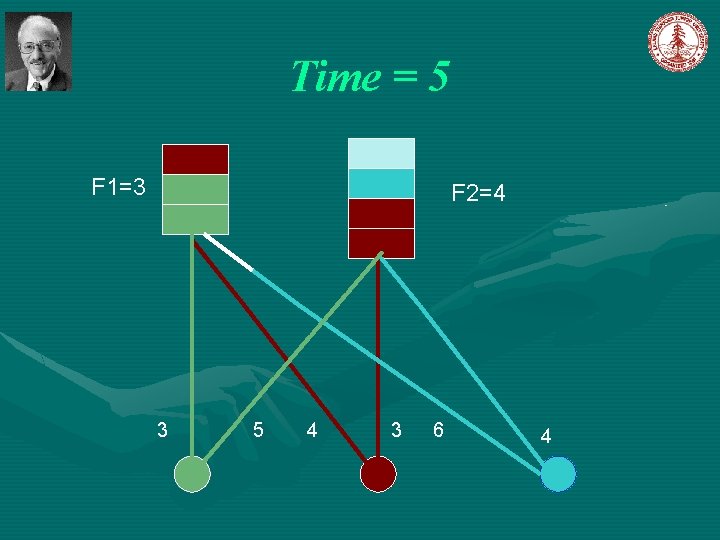
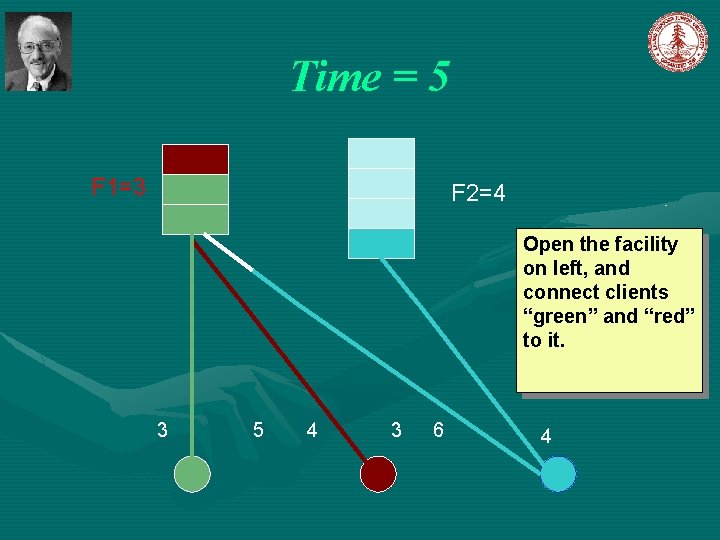
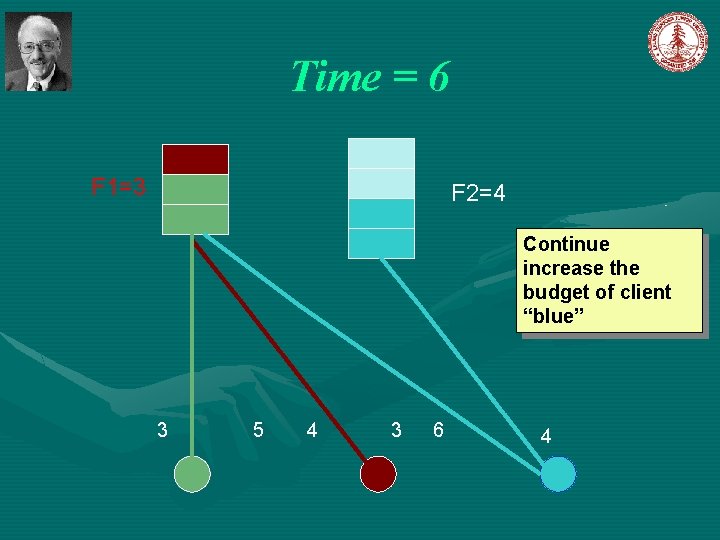
Simple Greedy Algorithm Jain et al [2003] Introduce a notion of time, such that each event can be associated with the time at which it happened. The algorithm start at time 0. Initially, all facilities are closed; all clients are unconnected; all set to 0. Let C=D While , increase simultaneously for all the following events occurs: , until one of (1). For some client , and a open facility then connect client j to facility i and remove j from C; (2). For some closed facility i, and connect client remove j from C. , then open with to facility i, and ,

Time = 0 F 1=3 F 2=4 3 5 4 3 6 4

Time = 1 F 1=3 F 2=4 3 5 4 3 6 4

Time = 2 F 1=3 F 2=4 3 5 4 3 6 4

Time = 3 F 1=3 F 2=4 3 5 4 3 6 4

Time = 4 F 1=3 F 2=4 3 5 4 3 6 4

Time = 5 F 1=3 F 2=4 3 5 4 3 6 4

Time = 5 F 1=3 F 2=4 Open the facility on left, and connect clients “green” and “red” to it. 3 5 4 3 6 4

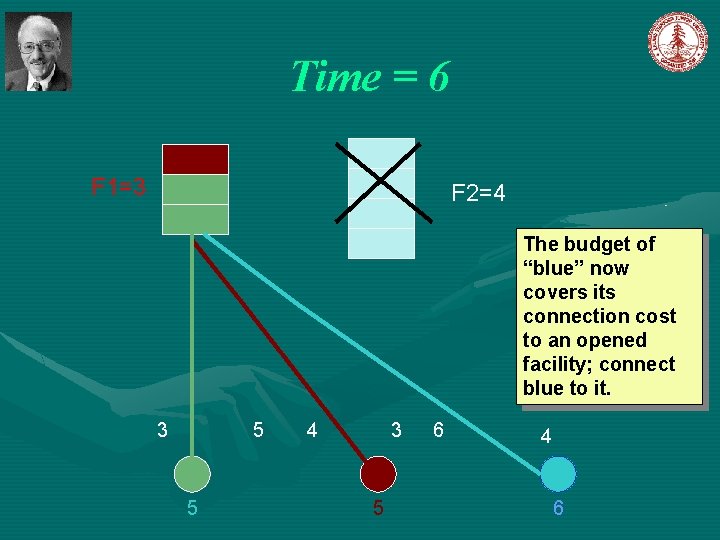
Time = 6 F 1=3 F 2=4 Continue increase the budget of client “blue” 3 5 4 3 6 4

Time = 6 F 1=3 F 2=4 The budget of “blue” now covers its connection cost to an opened facility; connect blue to it. 3 5 5 4 3 5 6 4 6

The Bi-Factor Revealing LP Jain et al [2003], Mahdian et al [2006] Given , is bounded above by Subject to: In particular, if

Approximation Results

Other Revealing LP Examples • N. Bansal et al. on “Further improvements in competitive guarantees for Qo. S buffering, ” 2004. • Mehta et al on “Adwords and Generalized Online Matching, ” 2005

Core of Cooperative Game • A set of alliance-proof allocations of profit (Scarf [1967]) • Deterministic game (using linear programming duality, Dantzig/Von Neumann [1948]) – Linear Production, MST, flow game, some location games (Owen [1975]), Samet and Zemel [1984], Tamir [1991], Deng et al. [1994], Feigle et al. [1997], Goemans and Skutella [2004], etc. ) • Stochastic game (using stochastic linear programming duality, Rockafellar and Wets [1976]) – Inventory game, Newsvendor (Anupindi et al. [2001], Muller et al. [2002], Slikker et al. [2005], Chen and Zhang [2006], etc. )

Outline • LP in Auction Pricing – Parimutuel Call Auction • Proving Theorems using LP – Uncapacitated Facility Location – Core of Alliance • Applications of LP Algorithms – Walras-Arrow-Debreu equilibrium – Linear Conic Programming • Photo Album of George

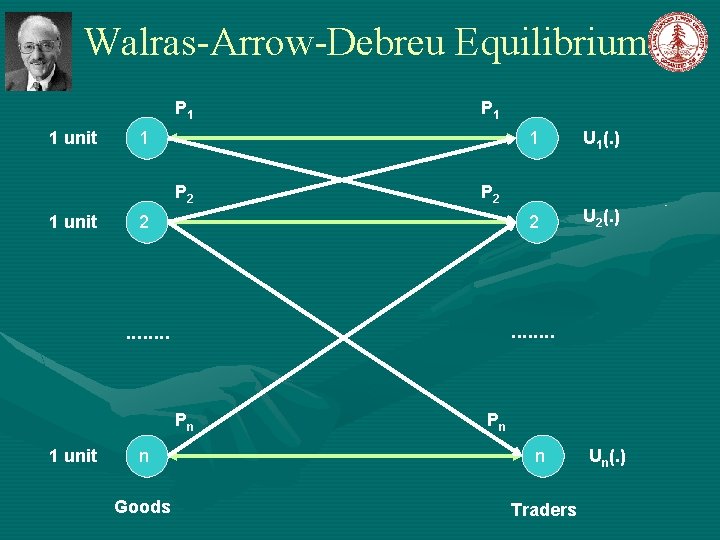
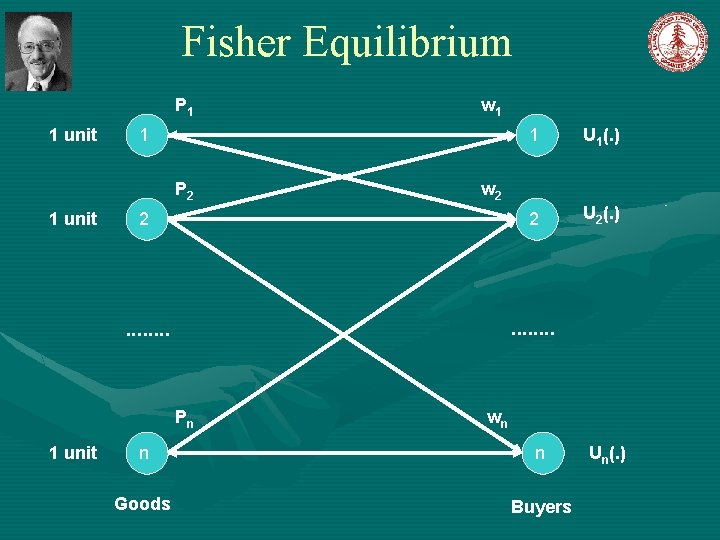
Walras-Arrow-Debreu Equilibrium The problem was first formulated by Leon Walras in 1874, Elements of Pure Economics, or the Theory of Social Wealth n players, each with • an initial endowment of a divisible good • utility function for consuming all goods—own and others. Every player 1. sells the entire initial endowment 2. uses the revenue to buy a bundle of goods such that his or her utility function is maximized. Walras asked: Can prices be set for all the goods such that the market clears? Answer by Arrow and Debreu in 1954: yes, under mild conditions if the utility functions are concave.

Walras-Arrow-Debreu Equilibrium P 1 1 unit 1 1 U 1(. ) 2 2 U 2(. ) . . . . P 2 1 unit Pn 1 unit P 1 P 2 Pn n n Goods Traders Un(. )

Fisher Equilibrium P 1 1 unit 1 1 U 1(. ) 2 2 U 2(. ) . . . . P 2 1 unit Pn 1 unit w 1 w 2 wn n n Goods Buyers Un(. )

Utility Functions

Equilibrium Computation Eisenberg and Gale [1959] , Scarf [1973], Eaves [1976, 1985] UtilityModel Fisher WAD Linear Convex Opt. LCP Leontief Convex Opt.

Equilibrium Computation Nenakhov and Primak [1983], Jain [2004] UtilityModel Fisher WAD Linear Convex Opt Leontief Convex Opt.

Equilibrium Computation [2004, 2005] UtilityModel Fisher WAD Linear LP-class Leontief LP-class*

Equilibrium Computation Codenotti et al. [2005], Chen and Deng [2005, 2006], UtilityModel Fisher WAD Linear LP-class Leontief LP-class* NP-Hard

Linear Conic Programming Many excellent sessions in ISMP 2006 …

Outline • LP in Auction Pricing – Parimutuel Call Auction – Core of Alliance • Proving Theorems using LP – Uncapacitated Facility Location • Applications of LP Algorithms – Walras-Arrow-Debreu equilibrium – Linear Conic Programming • Photo Album of George

Childhood Years

University Student Years

1967 Stanford OR

1975 National Medal of Science

1975 Nobel Laureate

1987 Student Graduation

2003 Science Fiction COMP IN OUR OWN IMAGE - a computer science odyssey by George B. Dantzig Nach, pale and shaking, rushed in to tell Adam, Skylab’s Captain, that a biogerm plague is sweeping the Earth, killing millions like flies. COMP In Our Own Image Copyright © 2003 by George Bernard Dantzig All rights reserved

2004 th 90 Birthday Party Organized by MS&E, Stanford, November 12, 2004 (Lustig, Thapa, etc)

2004 th 90 Birthday Party

2004 th 90 Birthday Party

LP/Dantzig Legacy Continues …

THE DANTZIG-LIEBERMAN OPERATIONS RESEARCH FELLOWSHIP FUND