Recent advances in Global Sensitivity Analysis techniques S

Recent advances in Global Sensitivity Analysis techniques S. Kucherenko Imperial College London, UK s. kucherenko@imperial. ac. uk 1

Outline Introduction of Global Sensitivity Analysis and Sobol’ Sensitivity Indices Why Quasi Monte Carlo methods (Sobol’ sequence sampling) are much more efficient than Monte Carlo (random sampling) ? Effective dimensions and their link with Sobol’ Sensitivity Indices Classification of functions based on global sensitivity indices Link between Sobol’ Sensitivity Indices and Derivative based Global Sensitivity Measures Quasi Randon Sampling - High Dimensional Model Representation with polynomial approximation Application of parametric GSA for optimal experimental design 2 France 2008
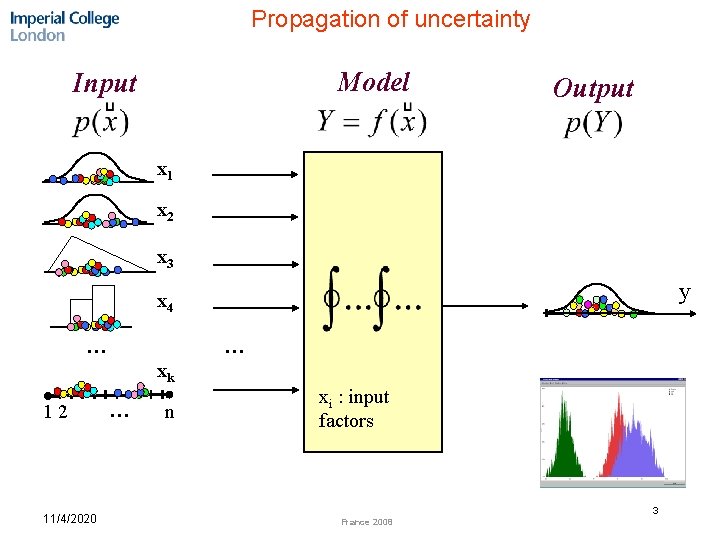
Propagation of uncertainty Model Input Output x 1 x 2 x 3 y x 4 … … xk 12 11/4/2020 … n xi : input factors 3 France 2008

Sensitivity Indices (SI) Consider a model x is a vector of input variables Y is the model output. ANOVA decomposition (HDMR): Variance decomposition: Sobol’ SI: 11/4/2020 4 France 2008

Sobol’ Sensitivity Indices (SI) n Definition: - partial variances - variance ¨ n Requires 2 n integral evaluations for calculations Sensitivity indices for subsets of variables: Introduction of the total variance: ¨ Corresponding global sensitivity indices: 5 France 2008

How to use Sobol’ Sensitivity Indices? accounts for all interactions between y and z, x=(y, z). n n The important indices in practice are and does not depend on ¨ does only depend on ¨ ; ; corresponds to the absence of interactions between ¨ and other variables ¨ n If then function has additive structure: Fixing unessential variables ¨ ¨ If does not depend on so it can be fixed complexity reduction, from to variables 6 France 2008

Evaluation of Sobol’ Sensitivity Indices Straightforward use of Anova decomposition requires 2 n integral evaluations – not practical ! There are efficient formulas for evaluation of Sobol’ Sensitivity Indices ( Sobol’ 1990): Evaluation is reduced to high-dimensional integration. Monte Carlo method is the only way to deal with such problems 7 France 2008

Original vrs Improved formulae for evaluation of Sobol’ Sensitivity Indices 8 France 2008

Improved formula for Sobol’ Sensitivity Indices 9 France 2008

Comparison deterministic and Monte Carlo integration methods 10 France 2008

Monte Carlo integration methods 11 France 2008

How to improve MC ? 12 France 2008

Sobol’ Sequences vrs Random numbers and regular grid Unlike random numbers, successive Sobol’ points “know" about the position of previously sampled points and fill the gaps between them 11/4/2020 13 France 2008

Quasi random sequences 14 France 2008
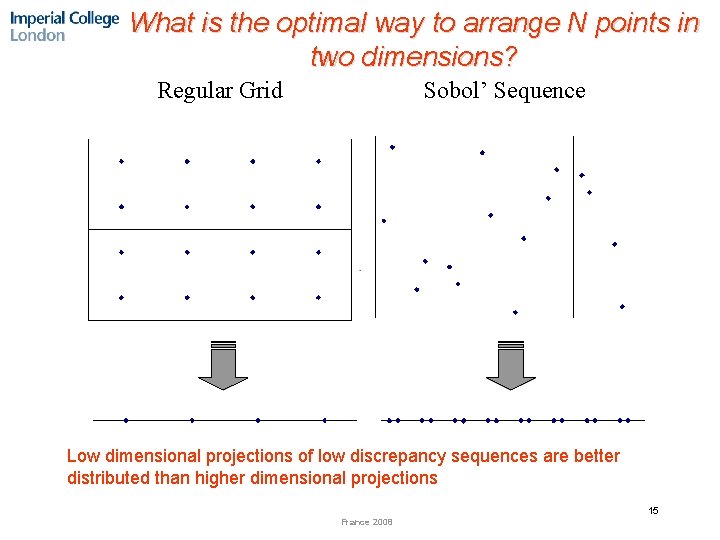
What is the optimal way to arrange N points in two dimensions? Regular Grid Sobol’ Sequence Low dimensional projections of low discrepancy sequences are better distributed than higher dimensional projections 15 France 2008

Comparison between Sobol sequences and random numbers 16 France 2008
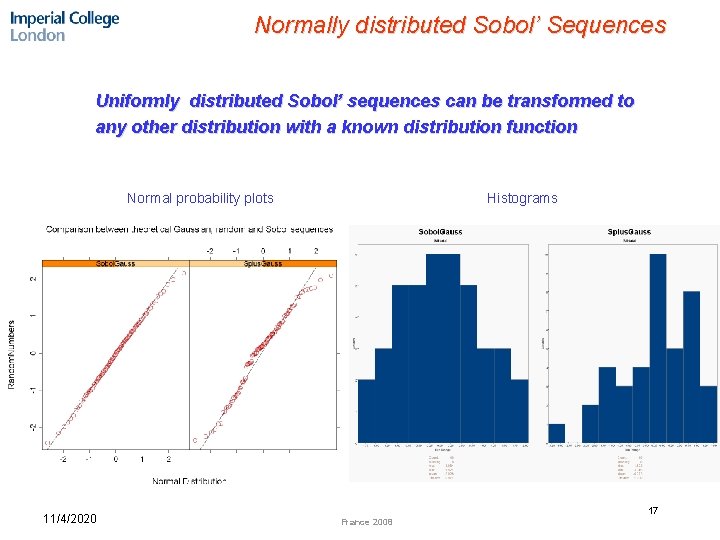
Normally distributed Sobol’ Sequences Uniformly distributed Sobol’ sequences can be transformed to any other distribution with a known distribution function Normal probability plots 11/4/2020 Histograms 17 France 2008

Are QMC efficient for high dimensional problems ? “For high-dimensional problems (n > 12), QMC offers no practical advantage over Monte Carlo” ( Bratley, Fox, and Niederreiter (1992)) ? ! 18 France 2008
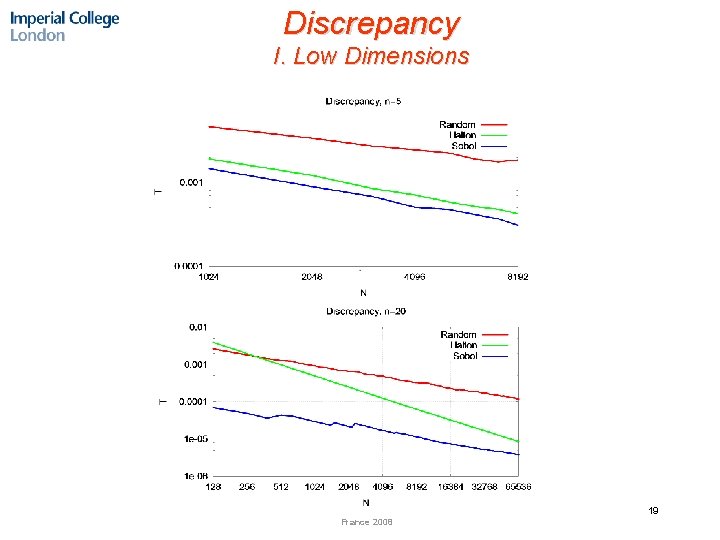
Discrepancy I. Low Dimensions 19 France 2008
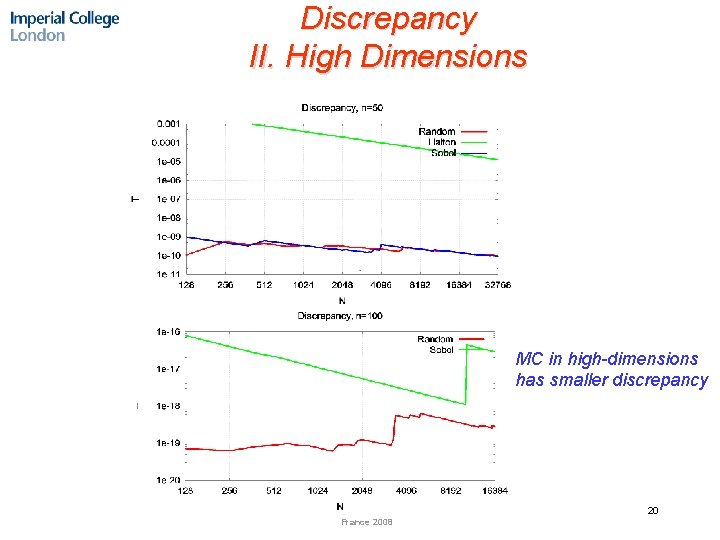
Discrepancy II. High Dimensions MC in high-dimensions has smaller discrepancy 20 France 2008

Is MC more efficient for high-dimensional problems than QMC ? ? n Pros: ¨MC in high-dimensions has smaller discrepancy ¨Some studies show degradation of the convergence rate of QMC methods in high-dimensions to O(1/√N) n Cons: Huge success of QMC methods in finance: QMC methods were proven to be much more efficient than MC even for problems with thousands of variables Many tests showed superior performance of QMC methods for high-dimensional integration 21 France 2008

Effective dimension ______________________________ 22 France 2008

Approximation errors For many problems only low order terms in the ANOVA decomposition are important Consider an approximation error Theorem 1: Link between an approximation error and effective dimension in superposition sense __________________________________ Set of variables can be regarded as not important if If and Consider an approximation error Theorem 2: Link between an approximation error and effective dimension in truncation sense 11/4/2020 23 France 2008
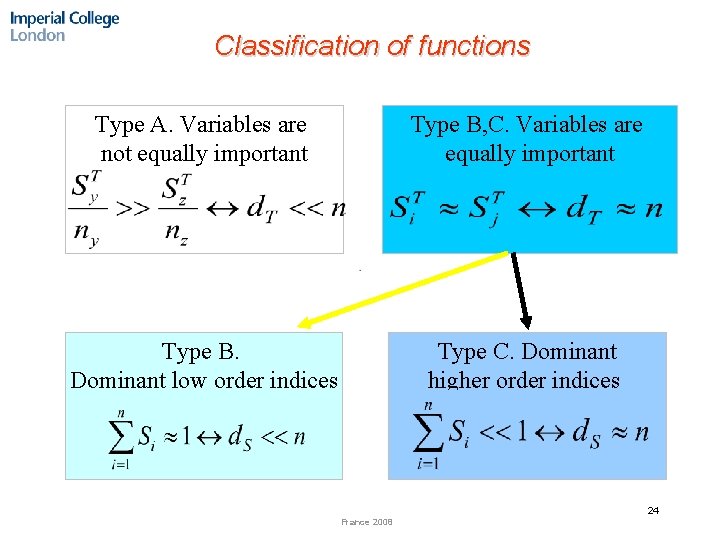
Classification of functions Type A. Variables are not equally important Type B, C. Variables are equally important Type B. Dominant low order indices Type C. Dominant higher order indices 24 France 2008

Sensitivity indices for type A functions 25 France 2008
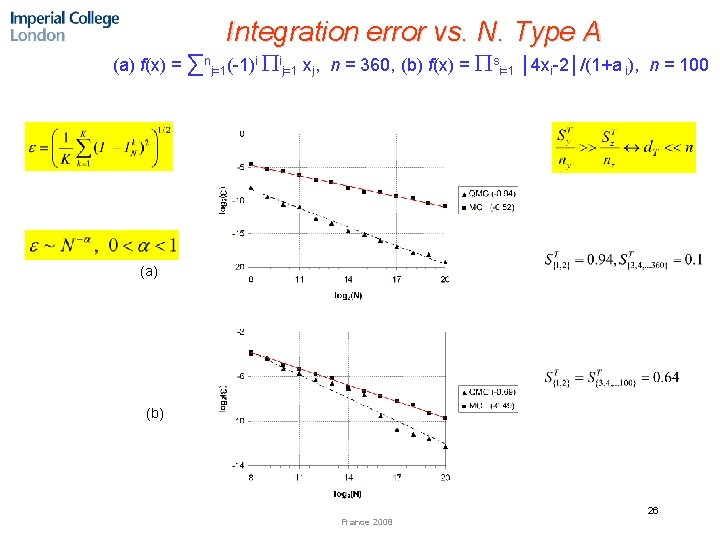
Integration error vs. N. Type A (a) f(x) = ∑nj=1(-1)i ij=1 xj, n = 360, (b) f(x) = si=1 │4 xi-2│/(1+a i), n = 100 (a) (b) 26 France 2008

Sensitivity indices for type B functions Dominant low order indices 27 France 2008
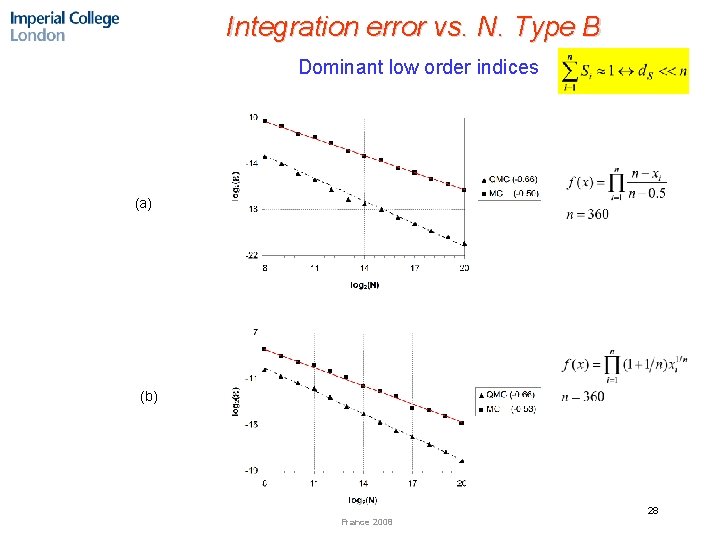
Integration error vs. N. Type B Dominant low order indices (a) (b) 28 France 2008

Sensitivity indices for type C functions Dominant higher order indices 29 France 2008

The integration error vs. N. Type C Dominant higher order indices: (a) (b) 30 France 2008
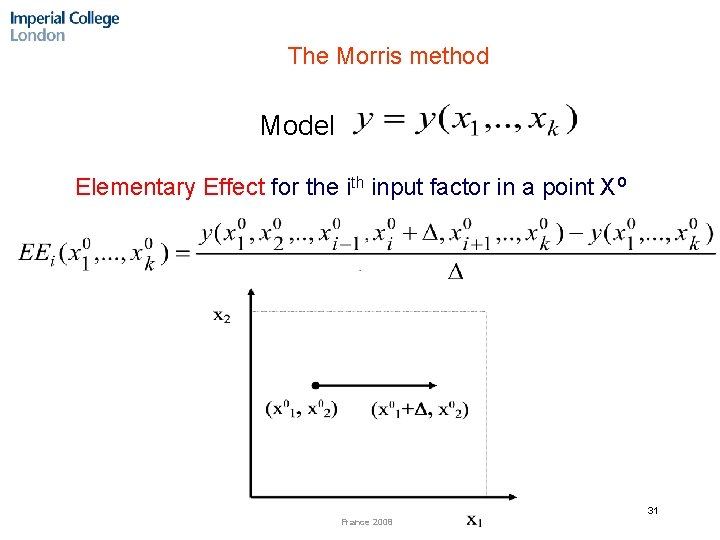
The Morris method Model Elementary Effect for the ith input factor in a point Xo 31 France 2008

The EEi is still a local measure Solution: take the average of several EE r elem. effects EE 1 i EE 2 i … EEri are computed at X 1 , … , Xr and then averaged. Average of EEi’s (xi) Standard deviation of the EEi’s σ (xi) 32 France 2008
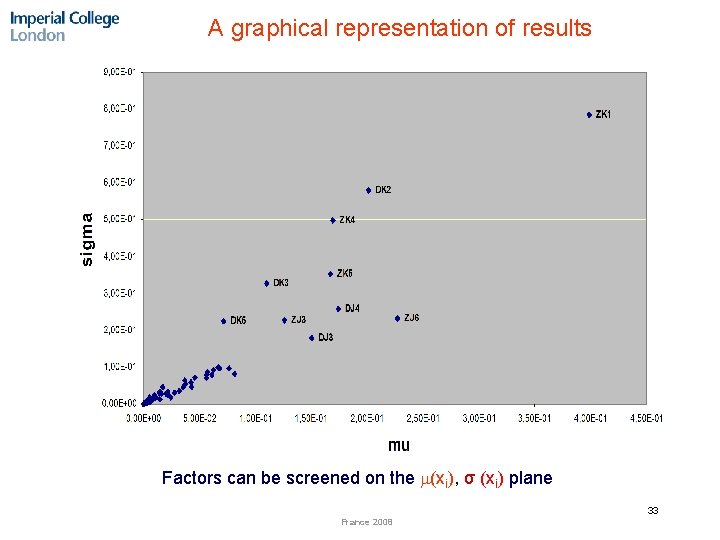
A graphical representation of results Factors can be screened on the (xi), σ (xi) plane 33 France 2008
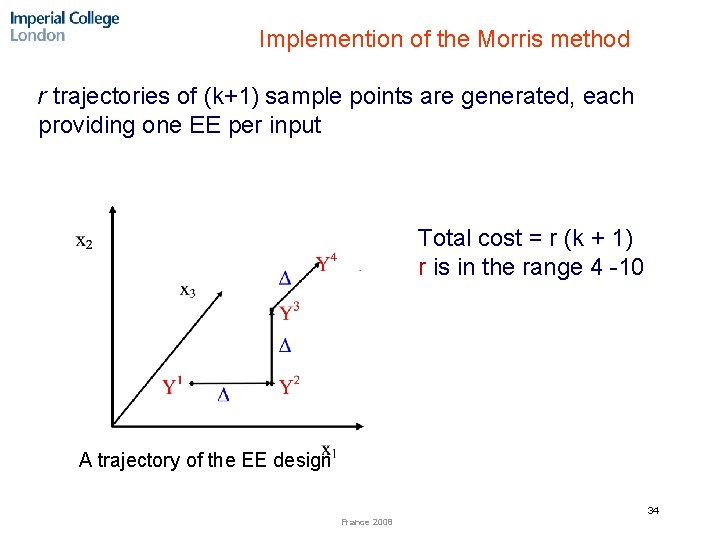
Implemention of the Morris method r trajectories of (k+1) sample points are generated, each providing one EE per input Total cost = r (k + 1) r is in the range 4 -10 A trajectory of the EE design 34 France 2008
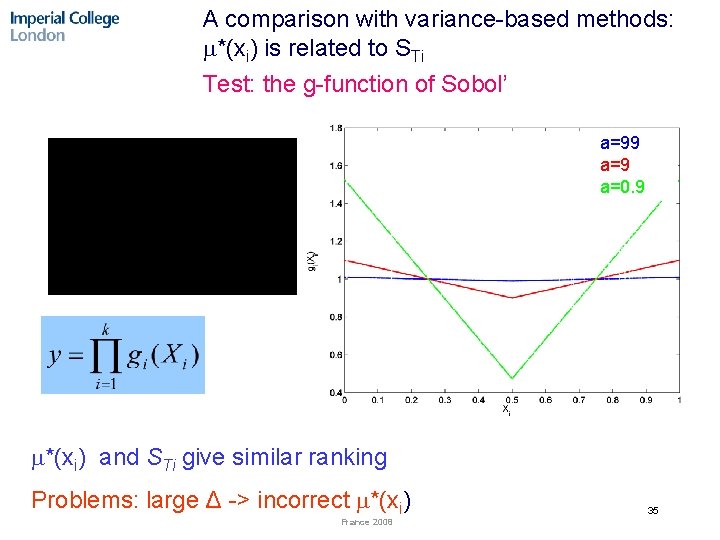
A comparison with variance-based methods: *(xi) is related to STi Test: the g-function of Sobol’ a=99 a=0. 9 *(xi) and STi give similar ranking Problems: large Δ -> incorrect *(xi) France 2008 35

Derivative based Global Sensitivity Measures Morris measure in the limit Δ → 0 Sample X 1 , … , Xr Sobol points, estimate finite differences E 1 i , E 2 i … Eri and then averaged. Average of Ei’s M*(xi) 36 France 2008
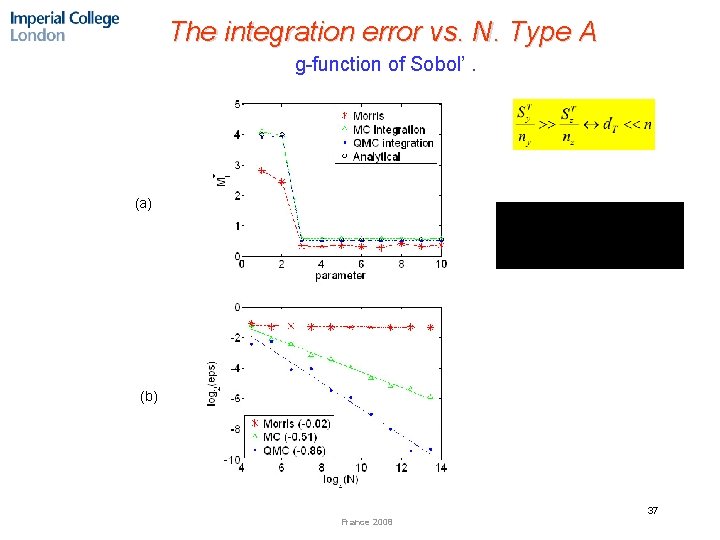
The integration error vs. N. Type A g-function of Sobol’. (a) (b) 37 France 2008
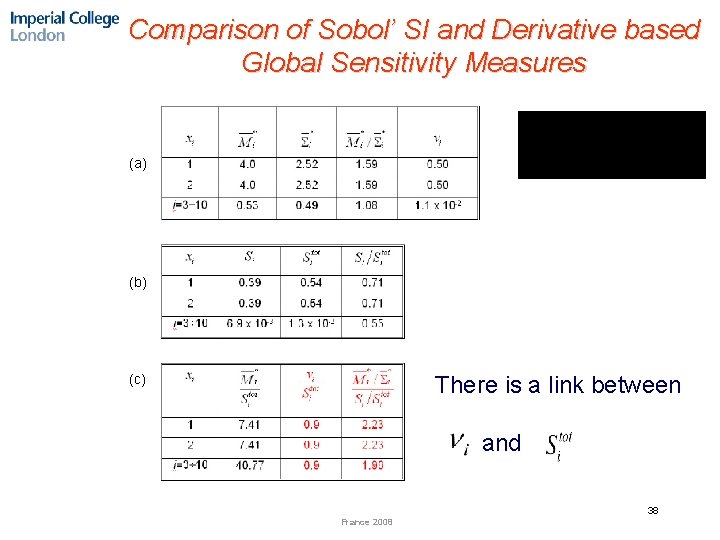
Comparison of Sobol’ SI and Derivative based Global Sensitivity Measures (a) (b) (c) There is a link between and 38 France 2008

Comparison of Sobol’ SI and Derivative based Global Sensitivity Measures 1. Small values of imply small values of . 2. For highly nonlinear functions ranking based on global SI can be very different from that based on derivative based sensitivity measures 39 France 2008

Quasi Randon Sampling HDMR For many problems only low order terms in the ANOVA decomposition are important. is a metamodel (HDMR), Rabitz et al: It is assumed that effective dimension in superposition sense ds=2. Sobol’ SI: 11/4/2020 40 France 2008

Polynomial Approximation Orthonormal polynomial base n Properties: n First few Legendre polynomials: 41 France 2008

Global Sensitivity Analysis (HDMR) n The number of function evaluations is n N(n+2) for original Sobol’ method n N for sensitivity indices based on RS-HDMR 42 France 2008
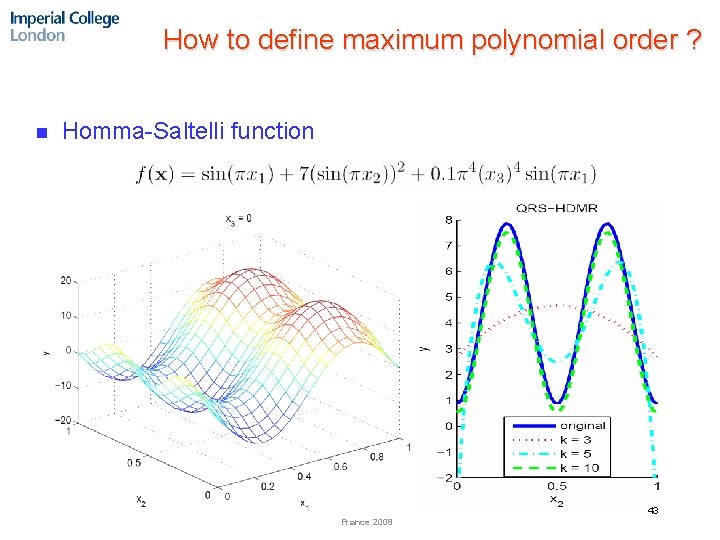
How to define maximum polynomial order ? n Homma-Saltelli function 43 France 2008
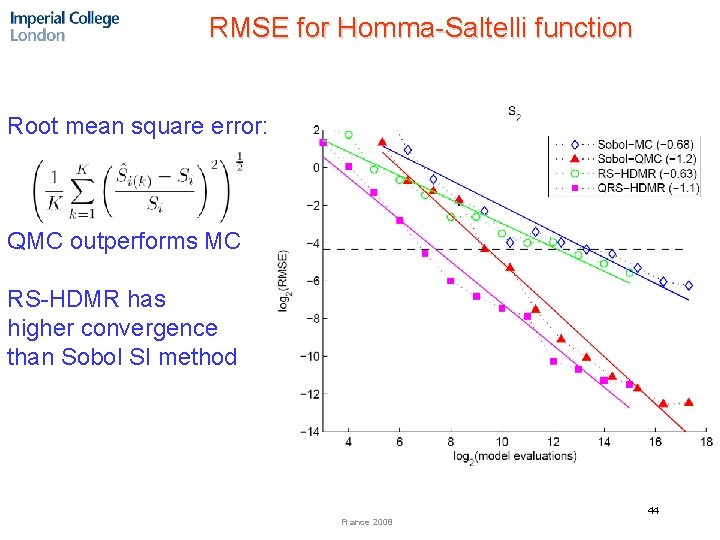
RMSE for Homma-Saltelli function Root mean square error: QMC outperforms MC RS-HDMR has higher convergence than Sobol SI method 44 France 2008
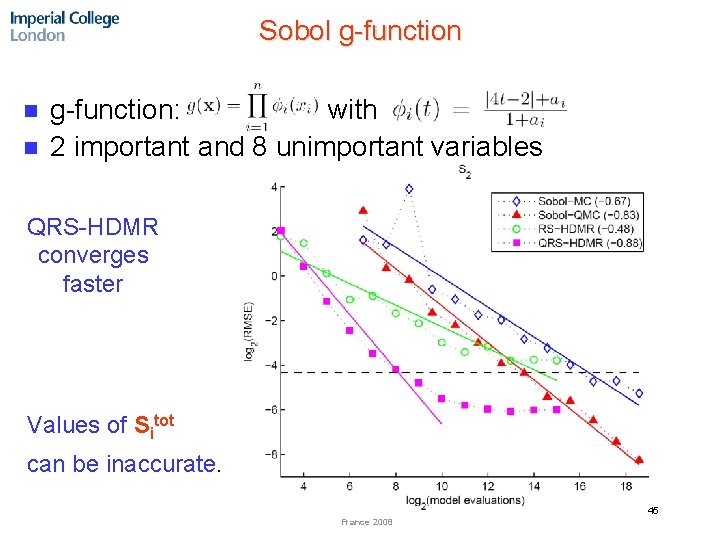
Sobol g-function n n g-function: with 2 important and 8 unimportant variables QRS-HDMR converges faster Values of Sitot can be inaccurate. 45 France 2008
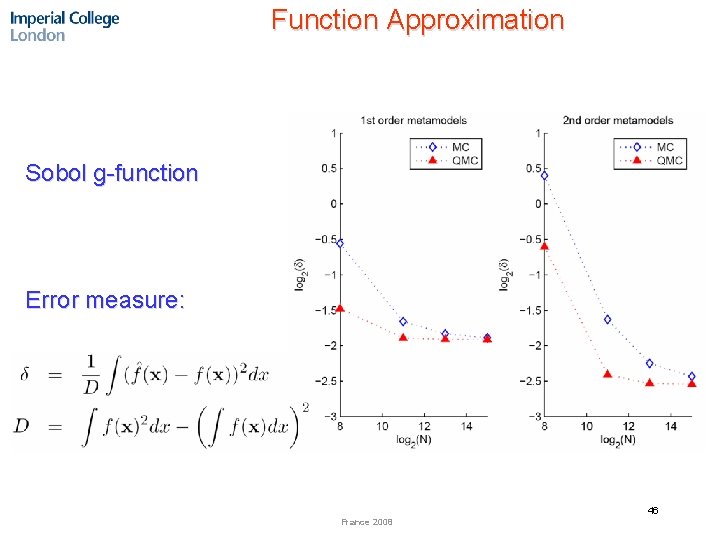
Function Approximation Sobol g-function Error measure: 46 France 2008

Computational costs QRS-HDMR method requires 10 to 103 times less model evaluations than Sobol SI method ! 47 France 2008

Optimal experimental design (OED) for parameter estimation Find values of experimentally manipulable variables (controls) and the time sampling strategy for a set of Nexp experiments which provides maximum information for the subsequent parameter estimation problem n subject to: n System dynamics (ODEs, DAEs) n Other algebraic constraints n Upper and lower bounds: Non-linear programming problem (NLP) with partial differential-algebraic (PDAEs) constraints 48 France 2008

Case study: fed-batch reactor n Biomass: • Parameters to be estimated: p 1, p 2 0. 05 < p 1 < 0. 98, 0. 05 < p 2 < 0. 98 n n Substrate: Reaction rate: • Control variables: u 1, u 2 Dilution factor: 0. 05 < u 1 < 0. 5 Feed substrate concentration: 5 < u 2 < 50 France 2008 49
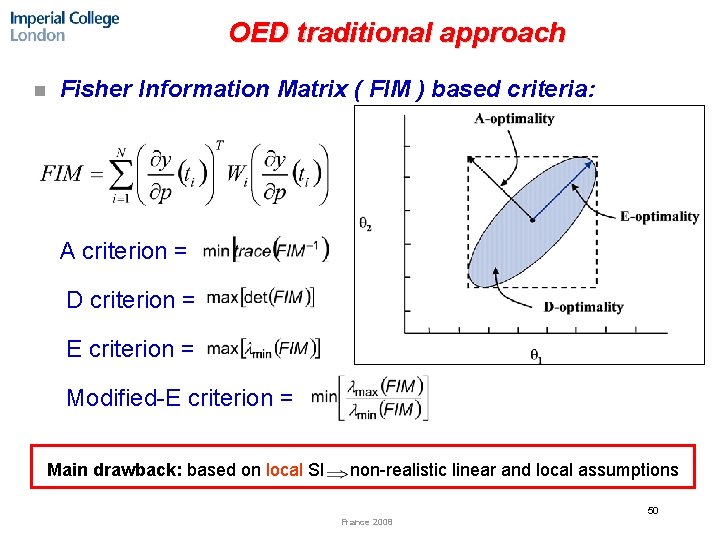
OED traditional approach n Fisher Information Matrix ( FIM ) based criteria: ¨ A criterion = ¨ D criterion = ¨ E criterion = ¨ Modified-E criterion = Main drawback: based on local SI non-realistic linear and local assumptions 50 France 2008

Parametric GSA • Optimal experimental design: identification of a set of experiments with conditions that deliver measurement data that are the most sensitive to the unknown parameters 51 France 2008

Application of Parametric GSA for parameter optimization Main advantage: based on global SI allows to consider a range of values for the parameters to be estimated n objective function: n Application of Global Optimization method France 2008 52

Case study: fed-batch reactor n Biomass: • Parameters to be estimated: p 1, p 2 0. 05 < p 1 < 0. 98, 0. 05 < p 2 < 0. 98 n n Substrate: Reaction rate: • Control variables: u 1, u 2 Dilution factor: 0. 05 < u 1 < 0. 5 Feed substrate concentration: 5 < u 2 < 50 France 2008 53
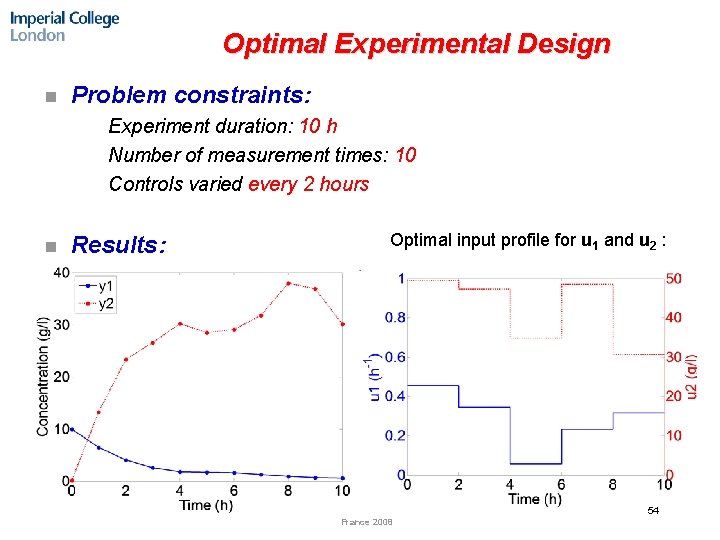
Optimal Experimental Design n Problem constraints: Experiment duration: 10 h ¨ Number of measurement times: 10 ¨ Controls varied every 2 hours ¨ ¨ n Results: Optimal input profile for u 1 and u 2 : 54 France 2008

Setting of the Parameter Estimation Problem n Steps to find p: n. Take experimental or generated pseudo-experimental points n. Maximum likelihood optimization p: set of parameters to be estimated : measurements variance n : model prediction : experimental measures Non-linear programming subject to: problem (NLP) with partial n System dynamics (ODEs, DAEs) n Other algebraic constraints differential-algebraic n Upper and lower bounds: (PDAEs) constraints 55 France 2008
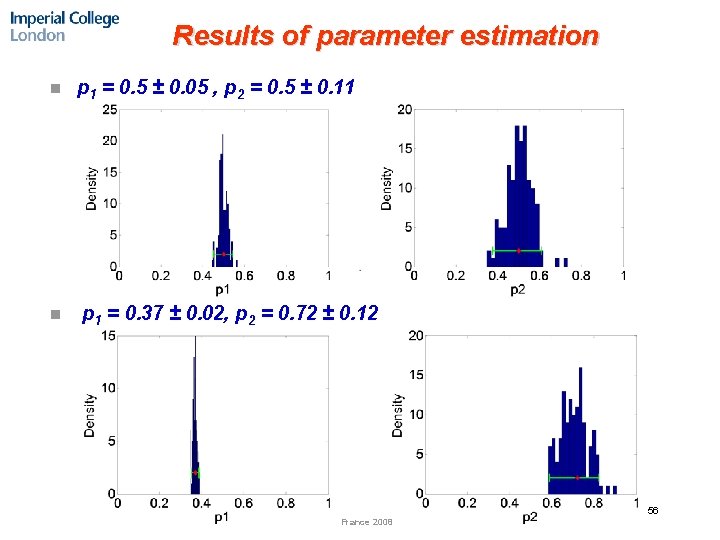
Results of parameter estimation n n p 1 = 0. 5 ± 0. 05 , p 2 = 0. 5 ± 0. 11 p 1 = 0. 37 ± 0. 02, p 2 = 0. 72 ± 0. 12 56 France 2008

Publications Hung WY, Kucherenko S. , Samsatli N. J. and Shah N. , The Proceedings of the 2003 Summer Computer Simulation Conference, Canada. Simulation Series, V 35, N 3, pp. 101 -106 (2003) Hung W. Y. , Kucherenko S. , Samsatli N. J. and Shah N (2004). Journal of the Operational Research Society 55, 801 -813. Sobol’ I. , Kucherenko S. Monte Carlo Methods and Simulation, 11, 1, 1 -9 (2005). Sobol’ I. , Kucherenko S. Wilmott, 56 -61, 1 (2005). Kucherenko S. , Shah N. Wilmott, 82 -91, 4 (2007). Sobol, I. M. , S. Tarantola, D. Gatelli, S. S. Kucherenko, W. Mauntz Reliability Engineering & System Safety, 957 -960, 92 (2007 ). Rodriguez-Fernandez M. , Kucherenko S. , Pantelides C. , Shah N. Proc. ESCAPE 17, V. Plesu and P. S. Agachi (Editors), p 66 -71, (2007) Kucherenko S. , Mauntz W. Submitted to Journal of Comp. Physics (2007). S. Kucherenko. Fifth International Conference on Sensitivity Analysis of Model Output, Budapest, (2007) S. Kucherenko, M. Rodriguez-Fernandez, C. Pantelides, N. Shah. Submitted to Reliability Engineering Systems Safety (2007) D. Gatelli, S. Kucherenko, M. Ratto, S. Tarantola, Submitted to Reliability Engineering Systems Safety (2007) I. M. Sobol’, S. Kucherenko. Submitted to Journal of Comp. Physics (2008). Application of Global Sensitivity Analysis to Biological Models A. Kiparissides, M. Rodriguez-Fernandez, S. Kucherenko, A. Mantalaris, E. Pistikopoulos Application of Global Sensitivity Analysis to Biological Models, Submitted to ESCAPE 18 (2008). 57 France 2008

Summary Quasi MC methods based on Sobol’ sequences outperform MC The error generated by the factors fixing is bounded by the total sensitivity index of the fixed factors Functions can be classified according to their effective dimension The method of derivative based global sensitivity measures (DGSM) is more efficient than the Morris and the Sobol’ SI methods. There is a link between DGSM and Sobol’ SI SI Quasi Randon Sampling - High Dimensional Model Representation with polynomial approximation can be orders of magnitude more efficient than Sobol’ SI for evaluation of main effects Application of global SI to OED results in the reduction of the required experimental work and the increased accuracy of parameter estimation 58 France 2008

Thank you for inviting me ! Acknowledgments Prof. Sobol’ Imperial College London, UK: N. Shah, M. Rodríguez Fernández, B. Feil, W. Mauntz, C. Pantelides Joint Research Centre, ISPRA, Italy: S. Tarantola, D. Gatelli, M. Ratto Financial support: EPSRC Grant EP/D 506743/1 59 France 2008
- Slides: 59