Recapitulate Proper length Proper frame of reference Proper







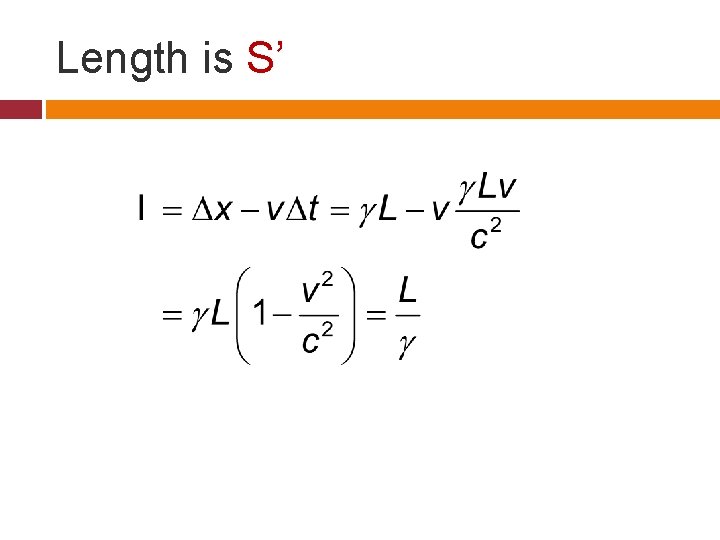


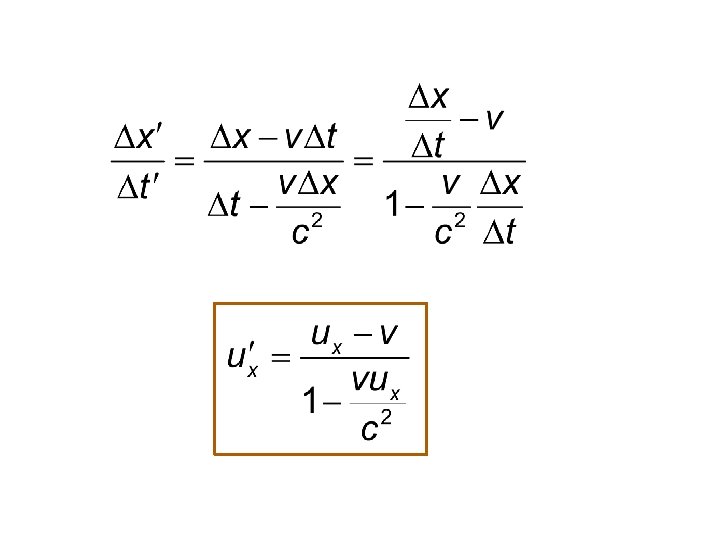
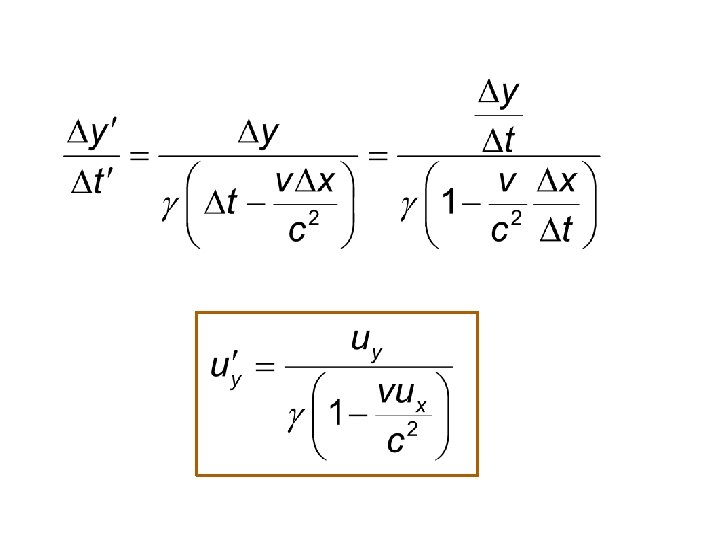










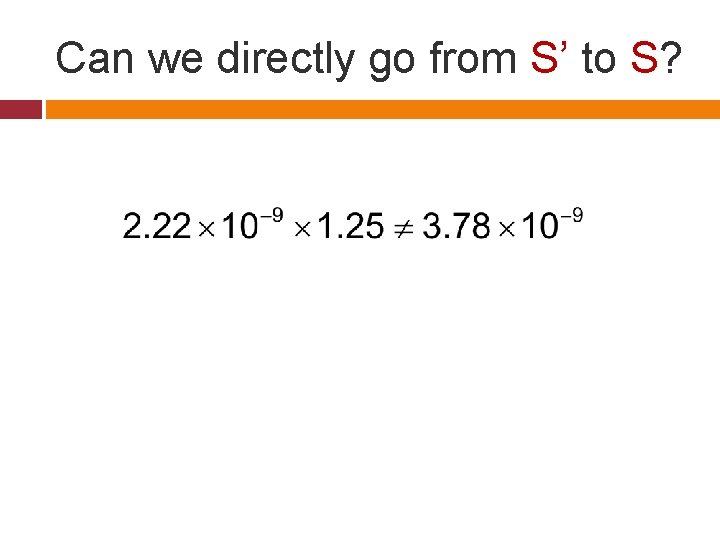






- Slides: 44

Recapitulate Proper length (ℓ). Proper frame of reference. Proper time interval (τ) Length Contraction Formula. Time Dilation Formula.

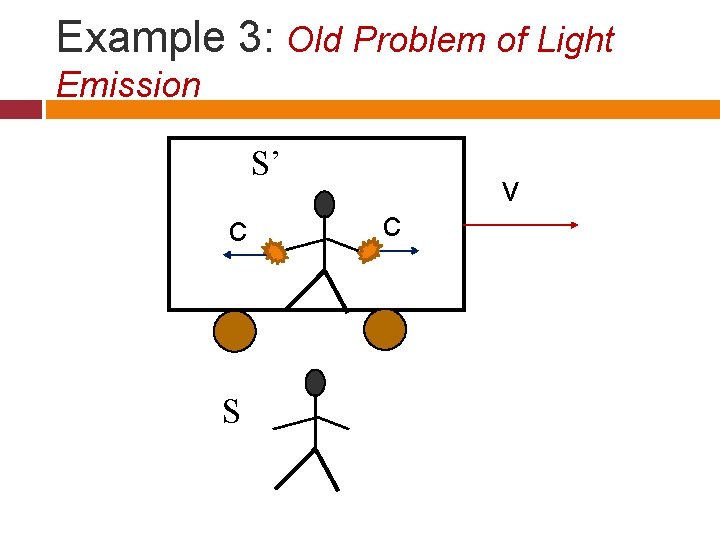
Example 3: Old Problem of Light Emission S’ c S c v

Events E 1: Light reaching front wall of the train. E 2: Light Reaching the back wall of the train.

S’ Frame There is no transformation required to write these equations. As before the two events are simultaneous.

Event 1 in S Frame Use Lorentz Inverse Transformation Assume that their origins were coincident, when light was emitted.

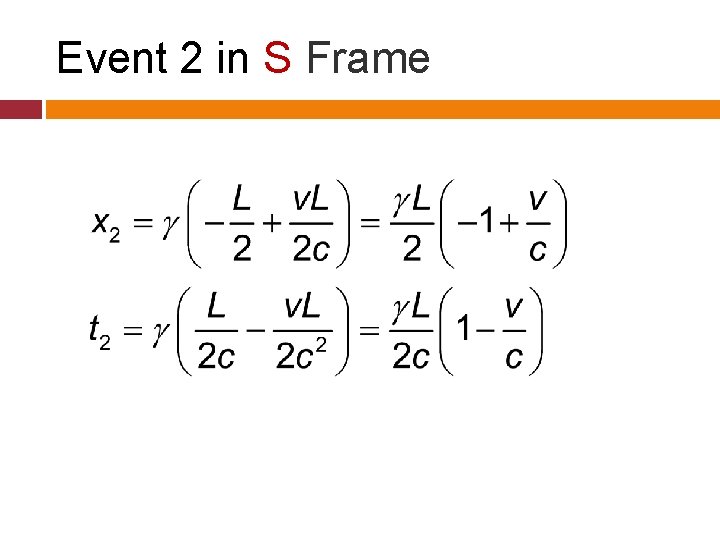
Event 2 in S Frame

Time Difference in S Frame E 2 occurs before E 1 as had been discussed earlier. The time interval between these two events is as follows.

Co-ordinate Difference The difference in co-ordinates of two events. Is it related to the length of compartment? In which frame the length is proper?

Length of train in S The x 2 -x 1 is overestimate of length of the train because the front end coordinate was measured later than the back end. Correct length is given as follows
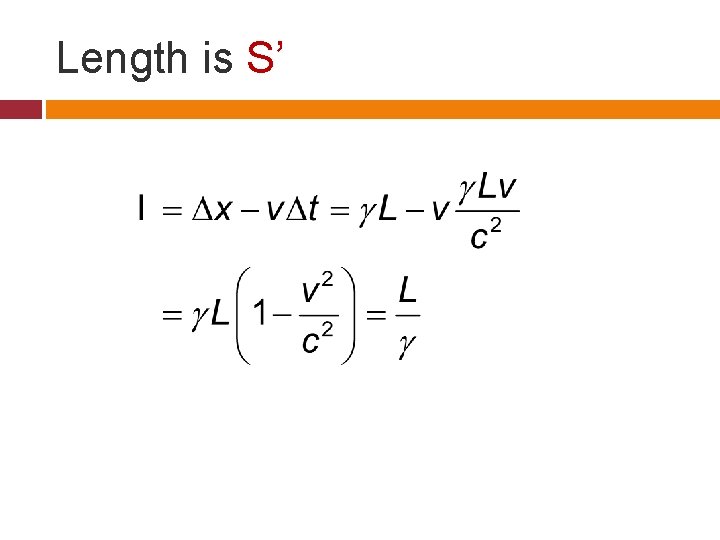
Length is S’

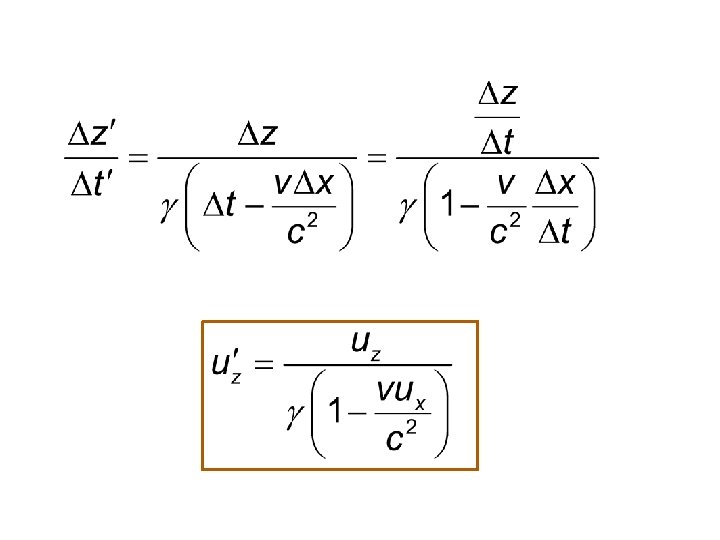
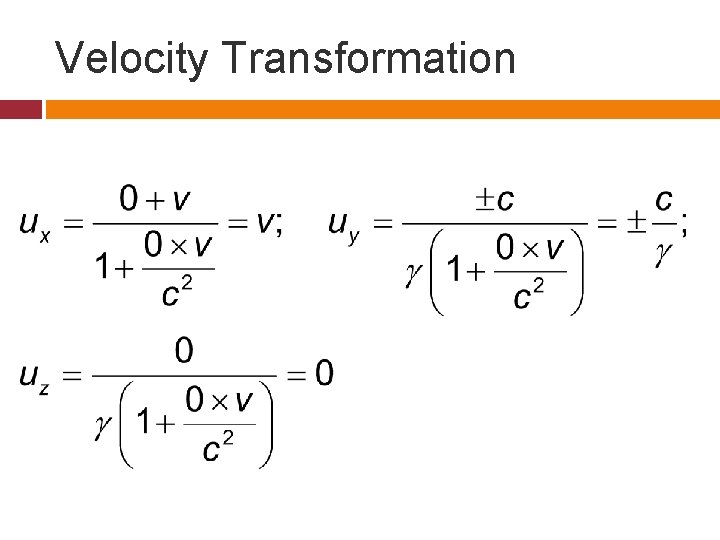
Velocity Transformation The velocity components are defined as follows.

Lorentz Transformation is differential form
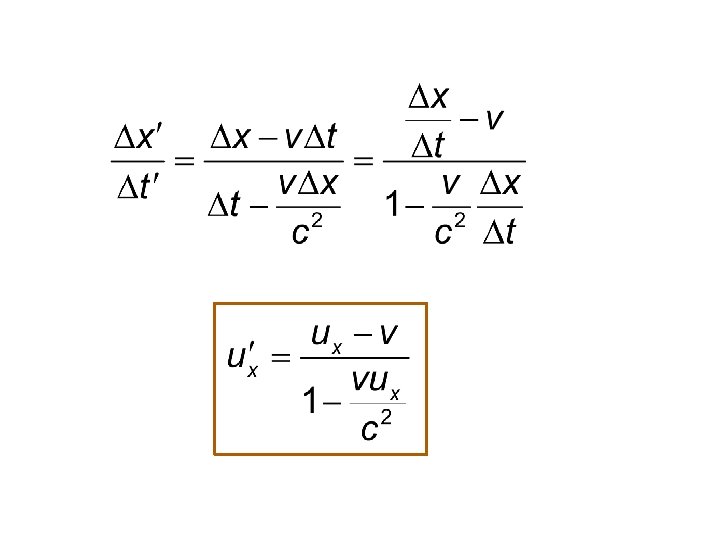
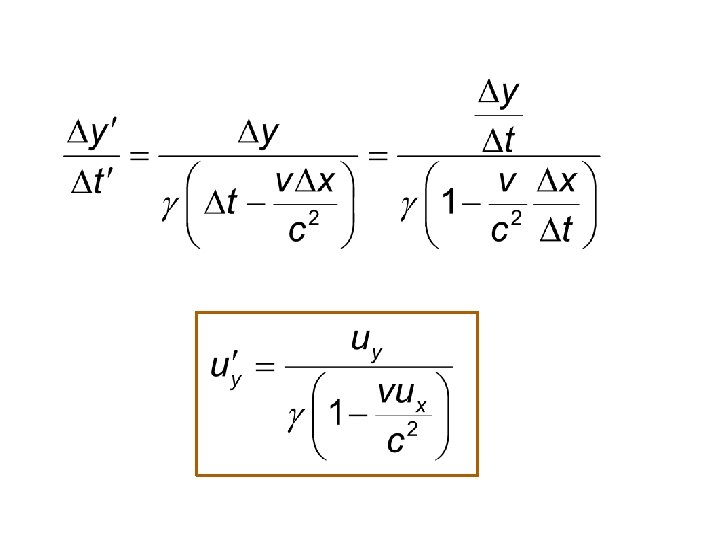


Velocity Transformation formula

Inverse Velocity Transformation

Comments One can show that �If u<c in S then u<c in S’ also �If u=c in S then u=c in S’ also �If u>c in S then u>c in S’ also

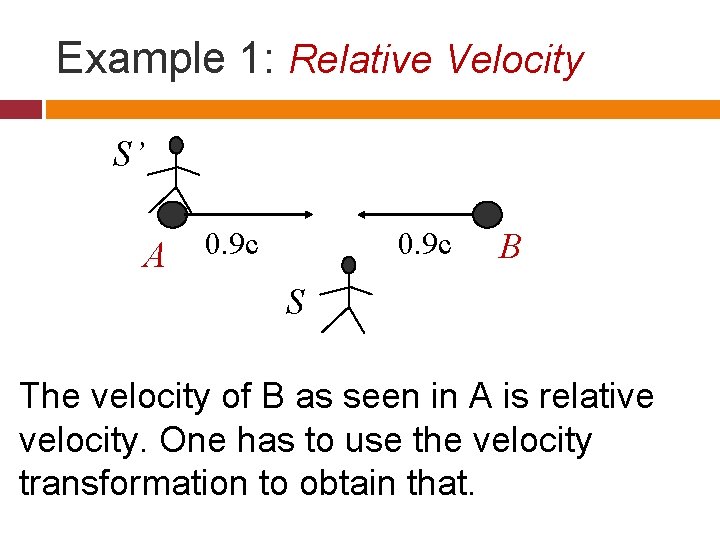
Example 1: Relative Velocity S’ A 0. 9 c B S The velocity of B as seen in A is relative velocity. One has to use the velocity transformation to obtain that.

Calculation Relative speed is smaller than c

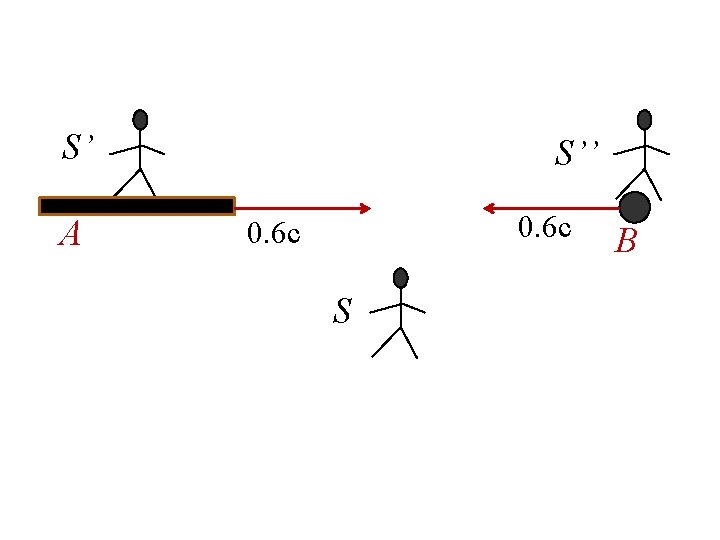
Example 2: A rod of proper length 1 meter is moving with a speed of 0. 6 c in +x direction as seen in frame S. In the same frame a particle is found to move in –x direction with the same speed. Find the time taken for the particle to cross the rod in (a) rod frame S’ (b) in the frame S” of particle and (c) in S frame.


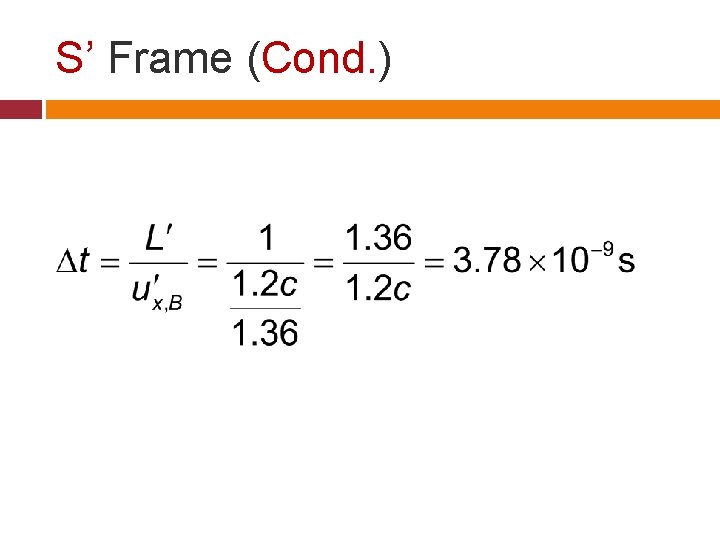
S’ Frame Speed of the particle B Length of the Rod

S’ Frame (Cond. )

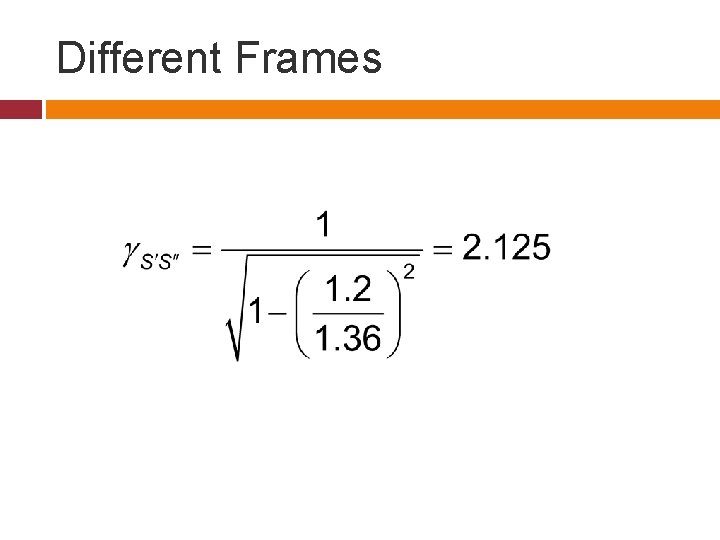
Different Frames

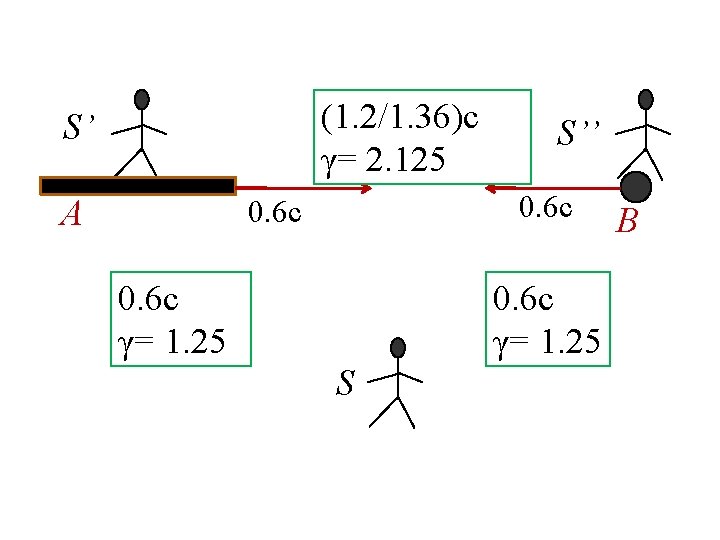
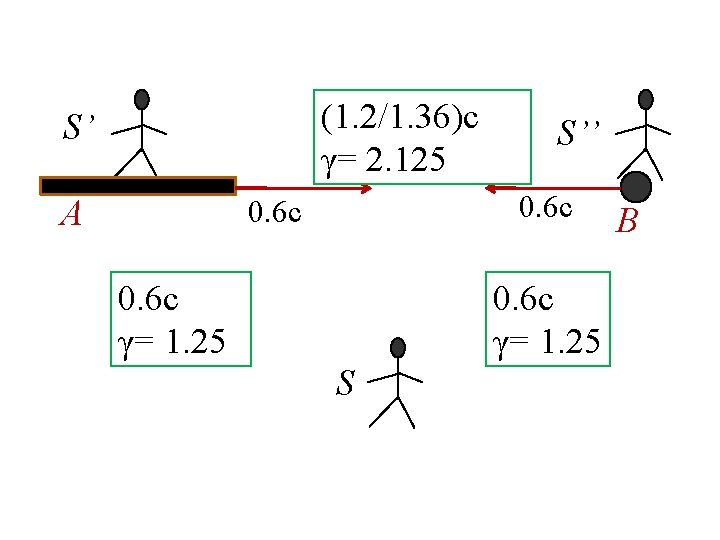
(1. 2/1. 36)c γ= 2. 125 S’ A S’’ 0. 6 c γ= 1. 25 S B

Define events E 1: Particle crossing front end of the rod E 2: Particle crossing back end of the rod

Look at time Is there a frame in which the time interval between the two events is proper?

S’’ Frame The time difference between the two events is proper, while in S’ it was dilated.

S Frame

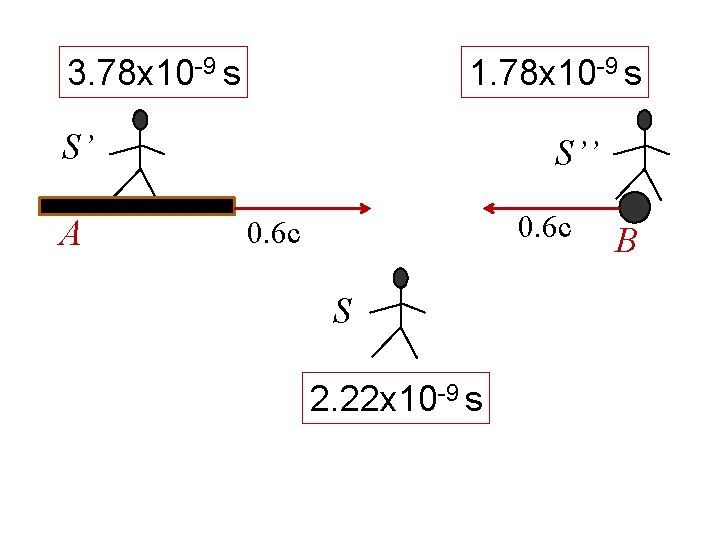
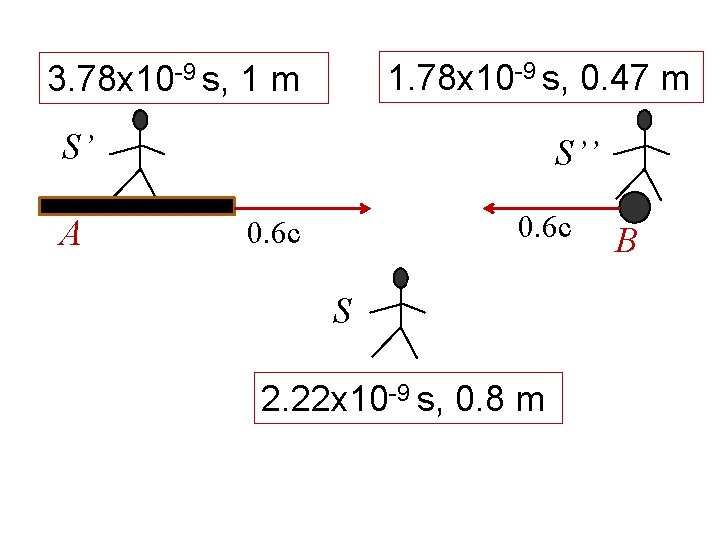
3. 78 x 10 -9 s 1. 78 x 10 -9 s S’ A S’’ 0. 6 c S 2. 22 x 10 -9 s B
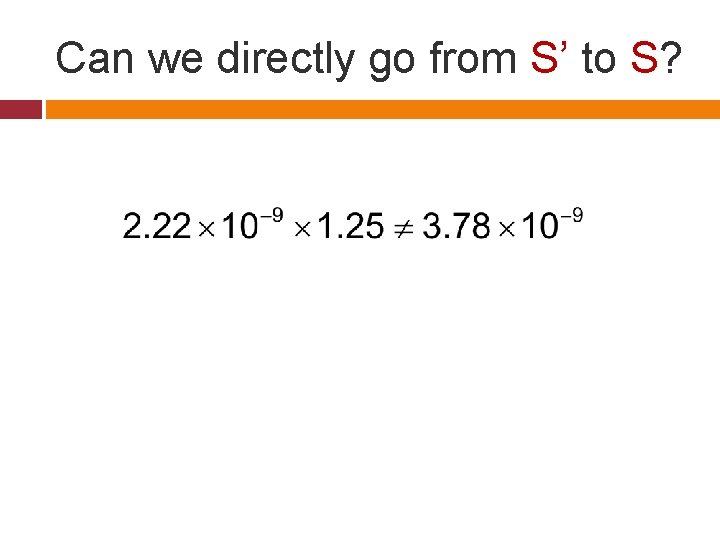
Can we directly go from S’ to S?

(1. 2/1. 36)c γ= 2. 125 S’ A S’’ 0. 6 c γ= 1. 25 S B

Second Method: Look at length Length of the rod in S” Length of the rod in S

1. 78 x 10 -9 s, 0. 47 m 3. 78 x 10 -9 s, 1 m S’ A S’’ 0. 6 c S 2. 22 x 10 -9 s, 0. 8 m B

Time in S” Speed of the rod Hence time interval

Time in S

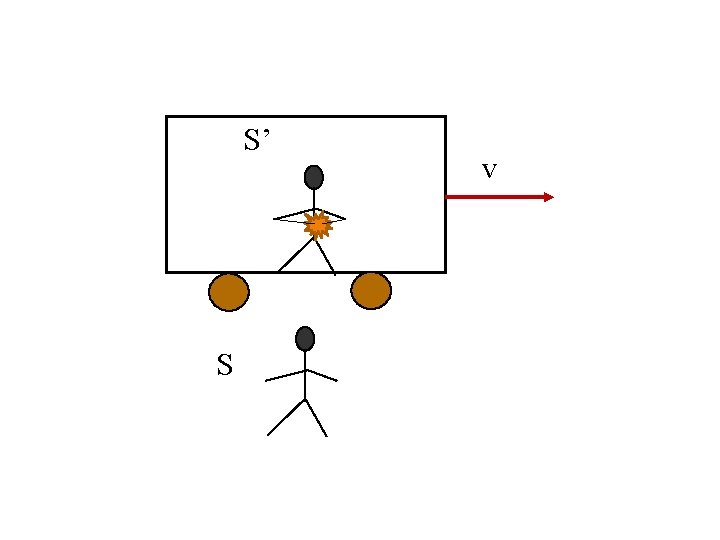
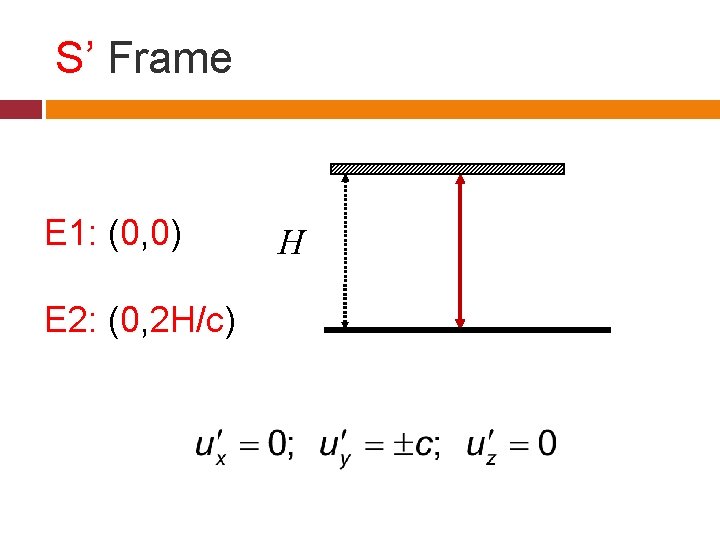
Example 3: Light Flashing in ydirection An observer in S’ flashes light in y’ direction from floor which gets reflected back from roof at height H and received at floor E 1: Light emitted from floor E 2: Light received at the floor

S’ S v

S’ Frame E 1: (0, 0) E 2: (0, 2 H/c) H

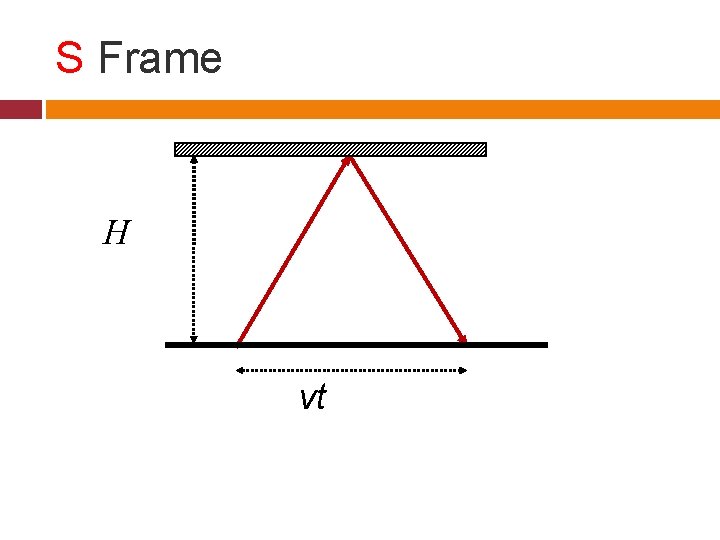
S Frame H vt

Velocity Transformation

Speed of light in S

Co-ordinates of the events in S E 1: (0, 0) E 2: (vt, t) What is t? Does it resemble time dilation formula?