Recap lecture 26 Example of nonregular language pumping

Recap lecture 26 Example of nonregular language, pumping lemma version I, proof, examples, 1

Pumping Lemma version II Statement: Let L be an infinite language accepted by a finite automaton with N states, then for all words w in L that have langth more than N, there are strings x, y and z ( y being non -null string) and length(x) + length(y) N s. t. w = xyz and all strings of the form xy. Nz are in L for n = 1, 2, 3, … Proof: The lemma can be proved, considering the following examples 2

Example Consider the language PALINDROME which is obviously infinite language. It has already been shown that the PALINDROME satisfies pumping lemma version I (previous version). To check whether the new version of pumping lemma still holds in case of the PALINDROME, let the PALINDROME be a regular language and be accepted by an FA of 78 states. Consider the word w = a 85 ba 85. 3

Example continued … Decompose w as xyz, where x, y and z are all strings belonging to * while y is non-null string, s. t. length(x) + length(y) 78, which shows that the substring xy is consisting of a’s and xyyz will become amore than 85 ba 85 which is not in PALINDROME. Hence pumping lemma version II is not satisfied for the language PALINDROME. Thus pumping lemma version II can’t be satisfied by any non regular language. Following is another example in this regard 4

Example Consider the language PRIME, of strings defined over Σ={a}, as {ap : p is prime}, i. e. PRIME = {aa, aaaaa, aaaaaaa, …} To prove this language to be nonregular, suppose contrary, i. e. PRIME is a regular language, then there exists an FA accepts the language PRIME. Let the number of states of this machine be 345 and choose a word w from PRIME with length more than 345, say, 347 i. e. the word w = a 347 5

Example continued … Since this language is supposed to be regular, therefore according to pumping lemma xynz, for n = 1, 2, 3, … are all in PRIME. Consider n=348, then xynz = xy 348 z = xy 347 yz. Since x, y and z consist of a’s, so the order of x, y, z does not matter i. e. xy 347 yz = xyzy 347 = a 347 y 347, y being non-null string and consisting of a’s it can be written y = am, m=1, 2, 3, …, 345. 6

Example continued … Thus xy 348 z = a 347 (am)347 = a 347(m+1) Now the number 347(m+1) will not remain PRIME for m = 1, 2, 3, …, 345. 348 Which shows that the string xy z is not in PRIME. Hence pumping lemma version II is not satisfied by the language PRIME. Thus PRIME is not regular. 7

Myhill Nerode theorem Strings belonging to same class: Consider a regular language L, defined over an alphabet . If, two strings x and y, defined over , are run over an FA accepting the language L, then x and y are said to belong to the same class if they end in the same state, no matter that state is final or not. Note: It is to be noted that this concept of strings x and y can be compared with indistinguishable strings w. r. t. L (discussed earlier). Equivalently, the strings x and y are said to belong to same class if for all strings z, either xz and yz belong to L or xz and yz don’t belong to L. 8

Myhill Nerode theorem continued … Statement: For a language L, defined over an alphabet , 1. L partitions * into distinct classes. 2. If L is regular then, L generates finite number of classes. 3. If L generates finite number of classes then L is regular. The proof is obvious from the following examples 9

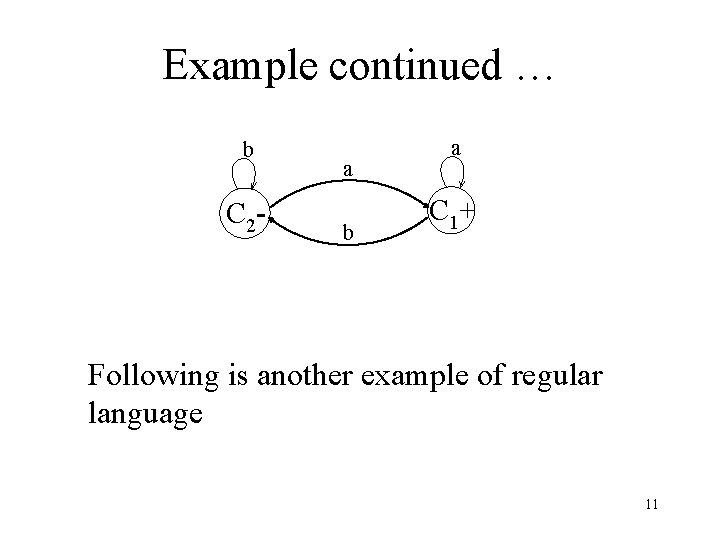
Example Consider the language L of strings, defined over ={a, b}, ending in a. It can be observed that L partitions * into the following two classes C 1 = set of all strings ending in a. C 2 = set of all strings not ending in a. Since there are finite many classes generated by L, so L is regular and hence following is an FA, built with the help of C 1 and C 2, accepting L. 10

Example continued … b C 2 - a b a C 1+ Following is another example of regular language 11

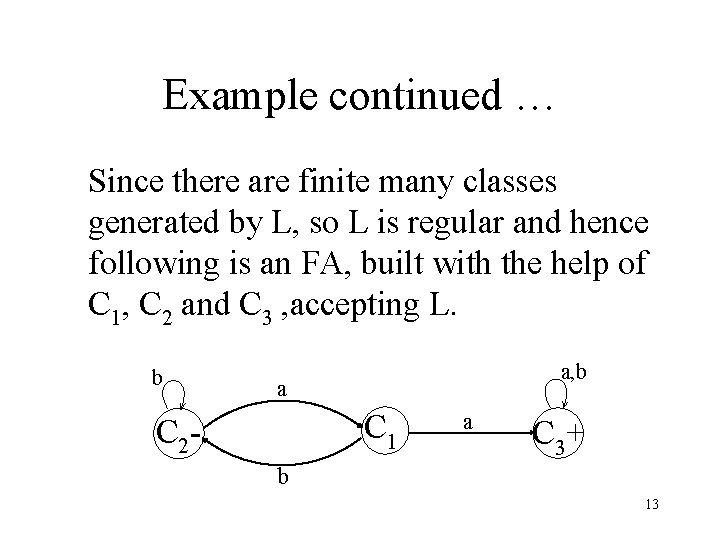
Example Consider the language L of strings, defined over ={a, b}, containing double a. It can be observed that L partitions * into the following three classes C 1 = set of all strings without aa but ending in a. C 2 = set of and all strings without aa but ending in b. C 3 = set of all strings containing aa. 12

Example continued … Since there are finite many classes generated by L, so L is regular and hence following is an FA, built with the help of C 1, C 2 and C 3 , accepting L. b a, b a C 1 C 2 - a C 3+ b 13

Instruction for Saad Slide #7 (PALINDROME) I have read a than 84 85 ba instead of a more than 85 ba more 85 14