RECAP Lecture 13 z Examples of Kleenes theorem

RECAP Lecture 13 z Examples of Kleene’s theorem part III (method 1) continued , Kleene’s theorem part III (method 2: Concatenation of FAs), z Example of Kleene’s theorem part III (method 2 : Concatenation of FAs) 1

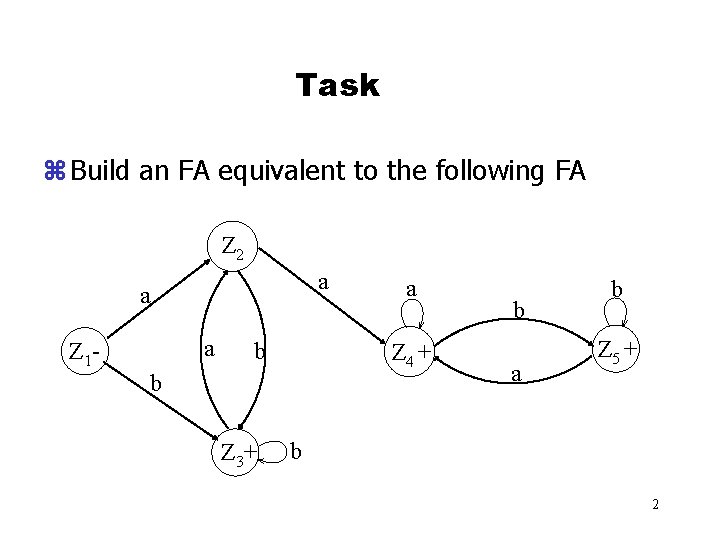
Task z Build an FA equivalent to the following FA Z 2 a a a Z 1 - b Z 4 + b Z 3+ a b Z 5 + b 2

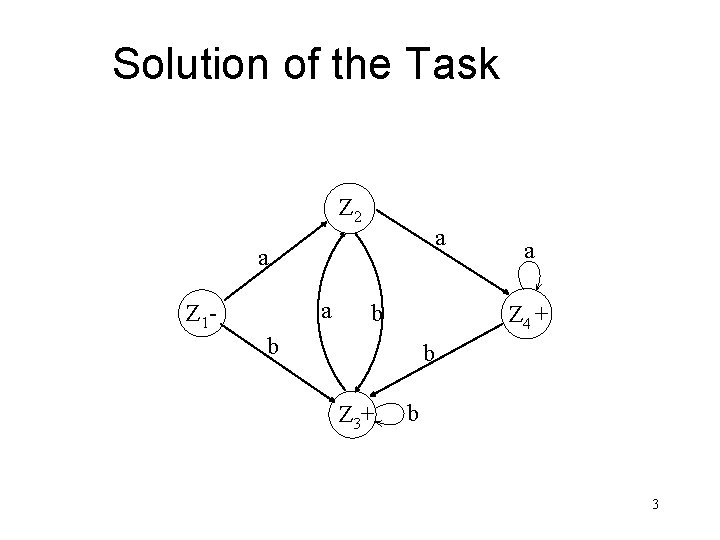
Solution of the Task Z 2 a a a Z 1 - b a Z 4 + b b Z 3+ b 3

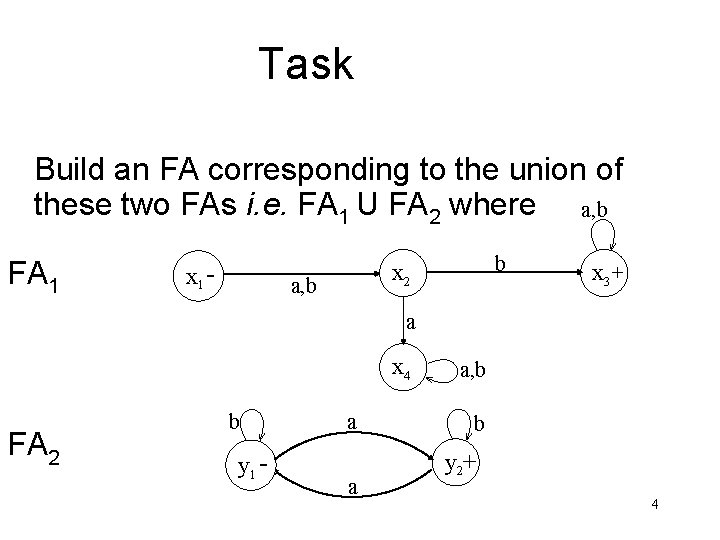
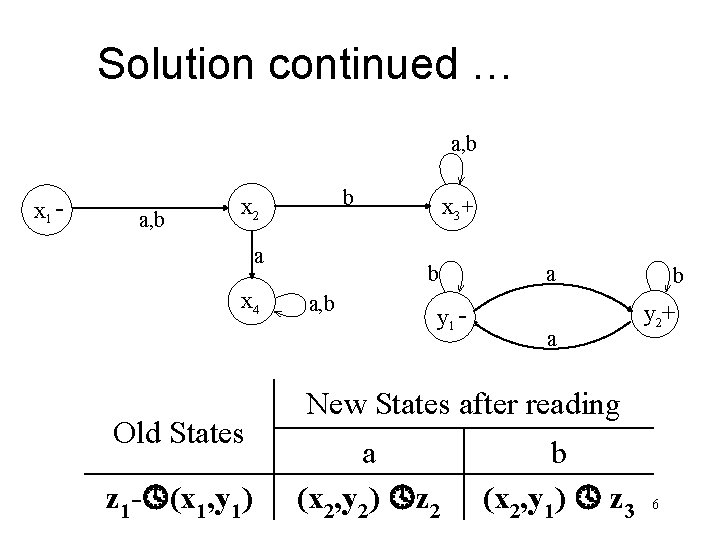
Task Build an FA corresponding to the union of these two FAs i. e. FA 1 U FA 2 where a, b FA 1 x 1 - b x 2 a, b x 3 + a x 4 FA 2 b y 1 - a a a, b b y 2+ 4

Task solution • RE corresponding to FA 1 may be (a+b)b(a+b)* which generates the language of strings, defined over Σ={a, b}, with b as second letter. • RE corresponding to FA 2 may be b*a(b+ab*a)* which generates the language of strings, defined over Σ={a, b}, with odd number of a’s. 5

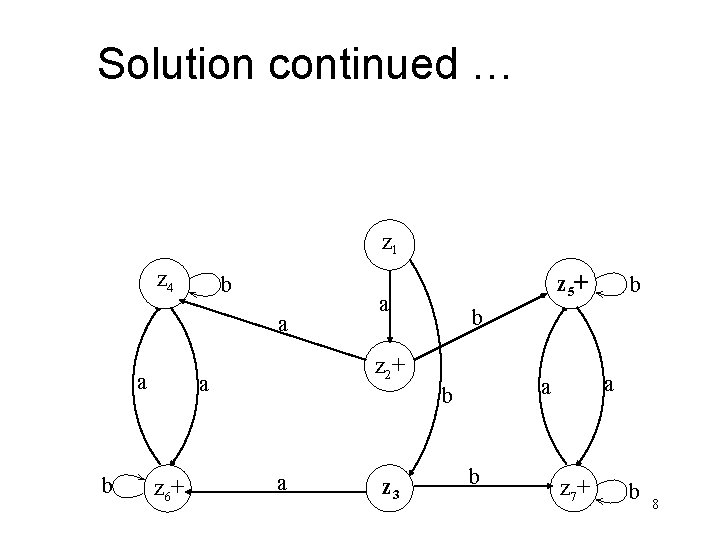
Solution continued … a, b x 1 - a, b b x 2 a x 4 Old States z 1 - (x 1, y 1) x 3 + b a, b y 1 - a a b y 2+ New States after reading a (x 2, y 2) z 2 b (x 2, y 1) z 3 6

Solution continued … Old States New States after reading a (x 4, y 1) z 4 z 2+ (x 2 , y 2) z 3 (x 2, y 1) (x 4, y 2) z 6 z 4 (x 4, y 1) (x 4, y 2) z 6 z 5+ (x 3, y 2) (x 3, y 1) z 7 z 67+ (x 43, y 21) (x (x 43, y 12) ) zz 54 b (x 3, y 2) z 5 (x 3, y 1) z 7 (x 4, y 1) z 4 (x 3, y 2) z 5 (x 43, y 21) z 67 7

Solution continued … z 1 z 4 b a a b a z 3 a a b b z 2+ a z 6+ z 5+ b z 7+ b 8

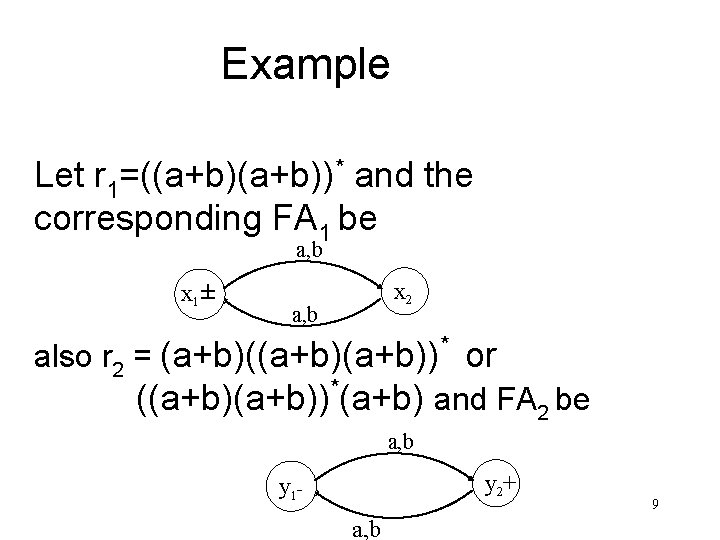
Example Let r 1=((a+b))* and the corresponding FA 1 be a, b x 1± x 2 a, b also r 2 = (a+b)(a+b))* or * ((a+b)) (a+b) and FA 2 be a, b y 2+ y 1 a, b 9

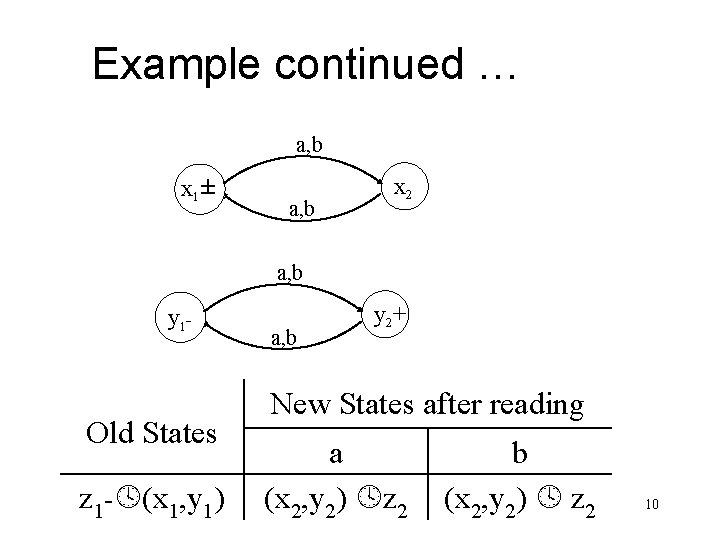
Example continued … a, b x 1± a, b x 2 a, b y 1 - Old States z 1 - (x 1, y 1) a, b y 2+ New States after reading a (x 2, y 2) z 2 b (x 2, y 2) z 2 10

Example continued … New States after Old States reading a b z 2+ (x 2, y 2 (x 1, y 1) z 1 (x 1, y 1) ) z 1 11

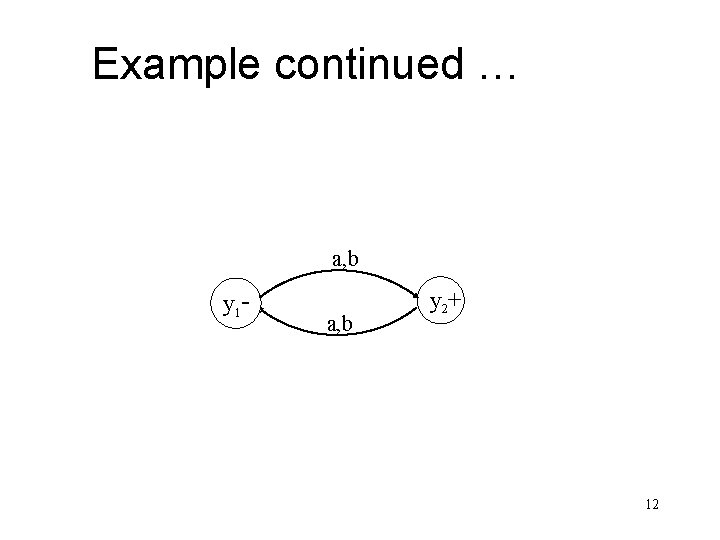
Example continued … a, b y 1 - a, b y 2+ 12

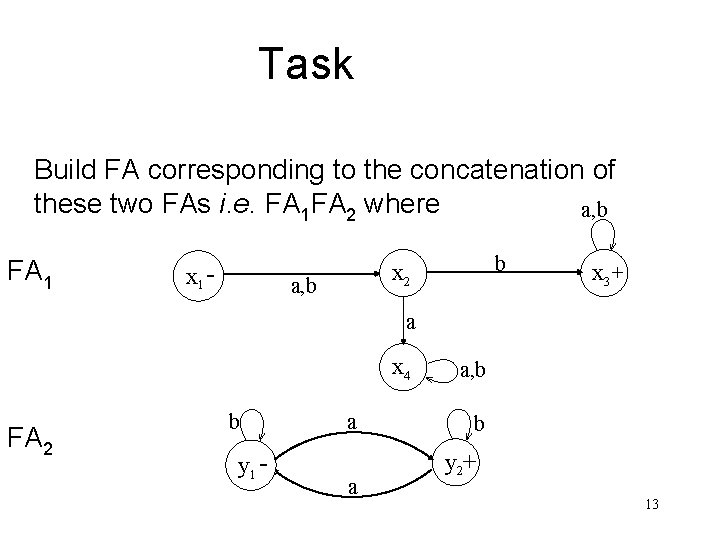
Task Build FA corresponding to the concatenation of these two FAs i. e. FA 1 FA 2 where a, b FA 1 x 1 - b x 2 a, b x 3 + a x 4 FA 2 b y 1 - a a a, b b y 2+ 13

Kleene’s Theorem Part III Continued … • Method 3: (Closure of an FA) Building an FA corresponding to r*, using the FA corresponding to r. It is to be noted that if the given FA already accepts the language expressed by the closure of certain RE, then the given FA is the required FA. However the method, in other cases, can be developed considering the following examples 14

Closure of FA Continued … Closure of an FA, is same as concatenation of an FA with itself, except that the initial state of the required FA is a final state as well. Here the initial state of given FA, corresponds to the initial state of required FA and a non final state of the required FA as well. 15

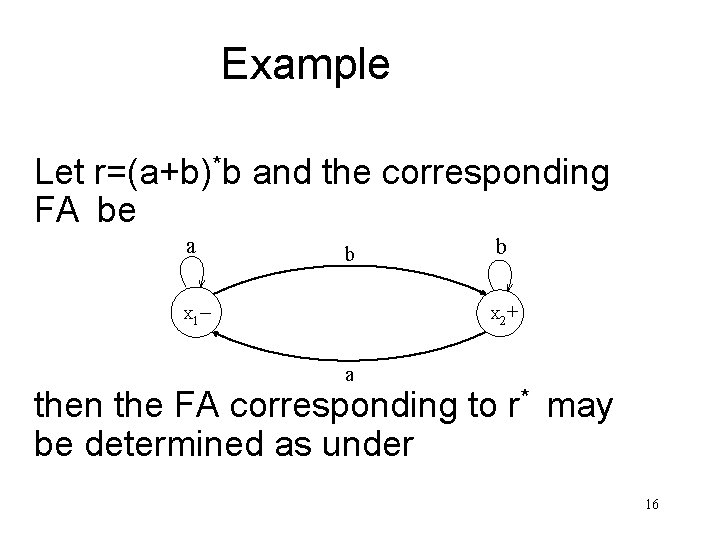
Example Let r=(a+b)*b and the corresponding FA be a b – b + X 1 X 2 a then the FA corresponding to r* may be determined as under 16

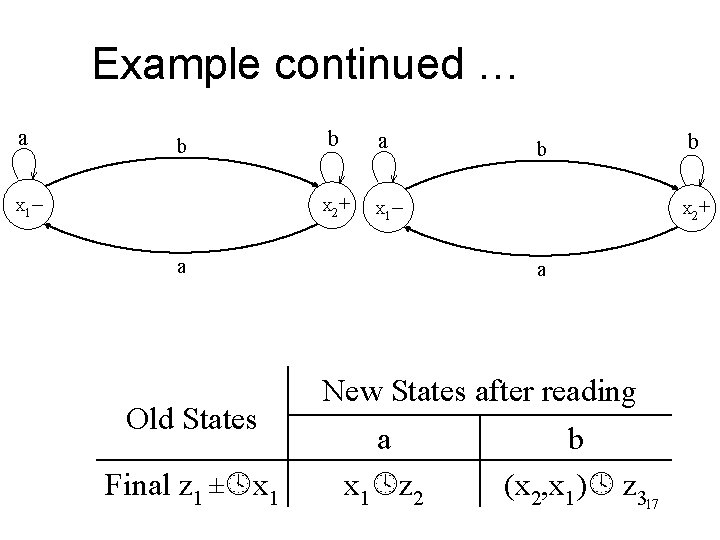
Example continued … a b – b a + X 1 X 2 b – Old States Final z 1 ± x 1 + X 1 a X 2 a New States after reading a x 1 z 2 b b (x 2, x 1) z 317

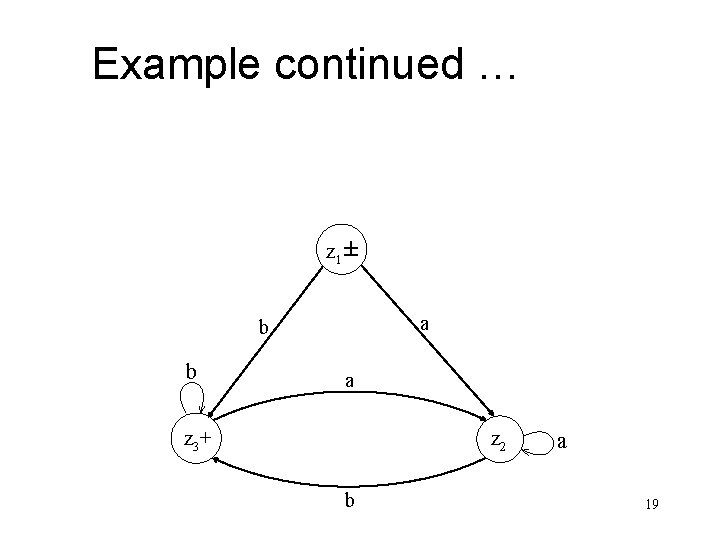
Example continued … Old States Non-final z 2 x 1 z 3+ (x 2, x 1) New States after reading a x 1 z 2 b (x 2, x 1) z 3 The corresponding transition diagram may be as under 18

Example continued … z 1± a b b a z 3+ z 2 b a 19

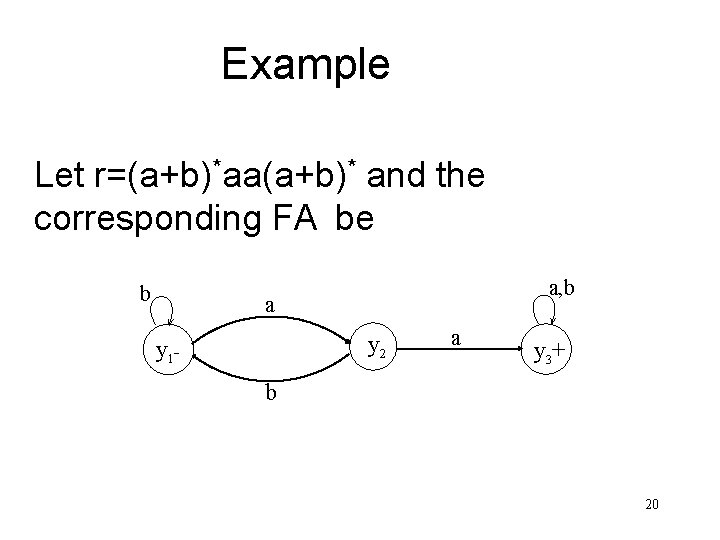
Example Let r=(a+b)*aa(a+b)* and the corresponding FA be b a, b a y 2 y 1 - a y 3+ b 20

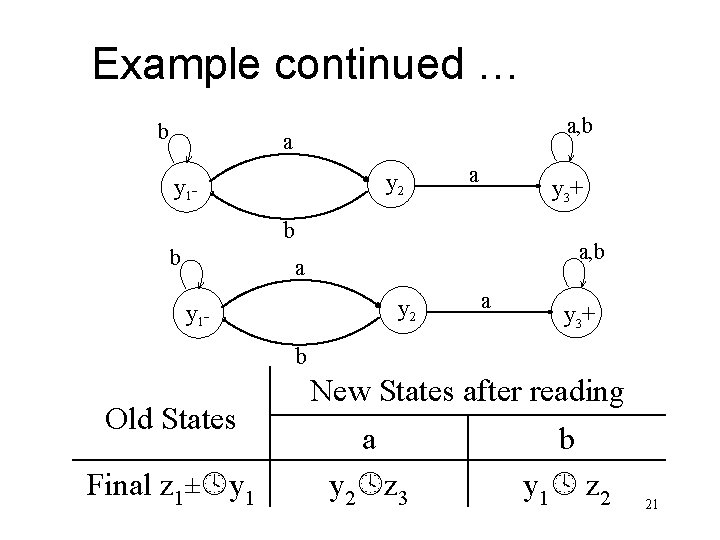
Example continued … b a, b a y 2 y 1 - a y 3+ b Old States Final z 1± y 1 New States after reading a y 2 z 3 b y 1 z 2 21

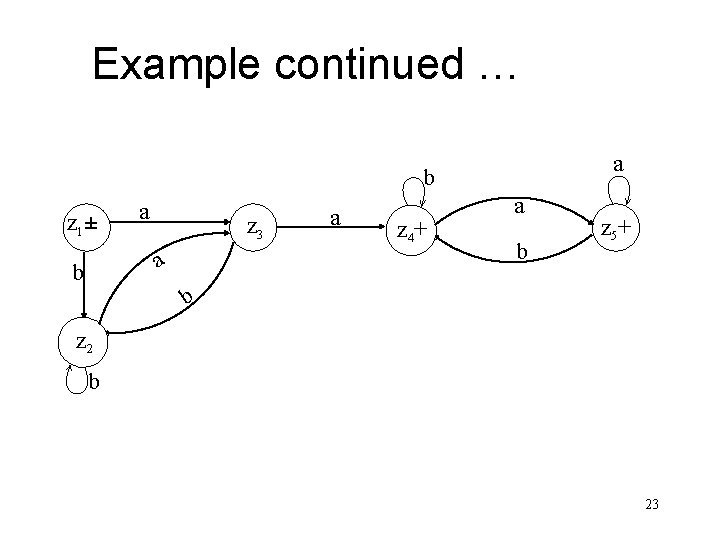
Example continued … Old States New States after reading a b z 2 y 1 y 2 z 3 y 1 z 2 z 3 y 2 (y 3, y 1) z 4 y 1 z 2 z 4+ (y 3, y 1) (y 3 , y 1, y 2) z 5 (y 3, y 1) z 4 z 5+ (y 3, y 1, y 2) (y 3, y 1 , y 2) z 5 (y 3, y 1) z 4 22

Example continued … a b z 1± a z 3 a b a z 4+ a b z 5+ b z 2 b 23

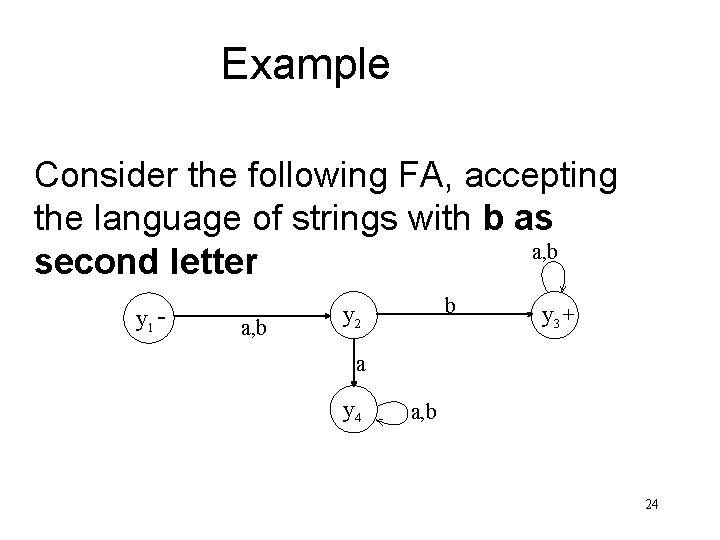
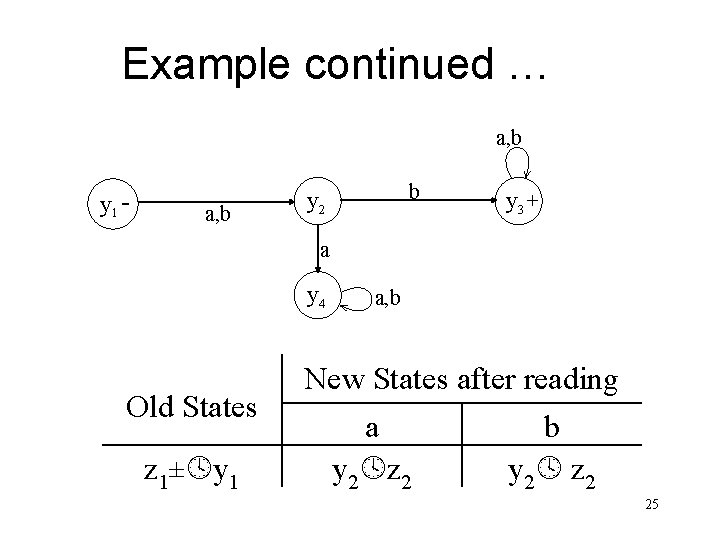
Example Consider the following FA, accepting the language of strings with b as a, b second letter y 1 - a, b b y 2 y 3 + a y 4 a, b 24

Example continued … a, b y 1 - a, b b y 2 y 3 + a y 4 Old States z 1± y 1 a, b New States after reading a y 2 z 2 b y 2 z 2 25

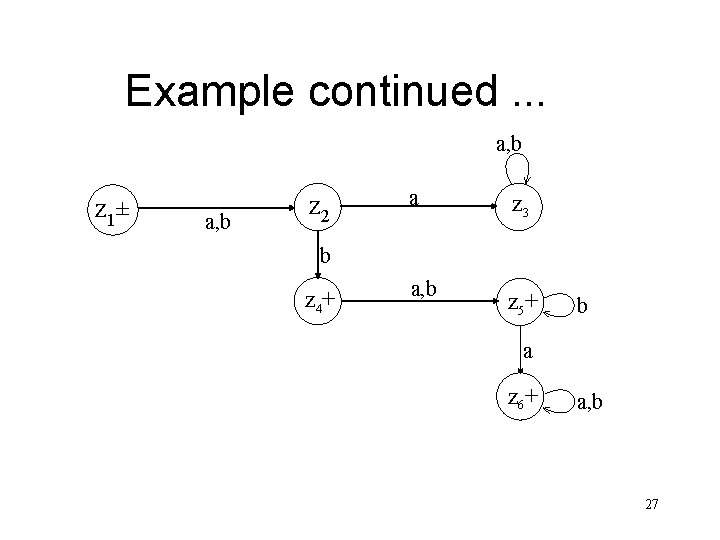
Example continued. . . Old States New States after reading a b z 2 y 4 z 3 (y 3, y 1) z 4 z 3 y 4 z 3 z 4+ (y 3, y 1) (y 3 , y 1 , y 2) z 5+ (y 3, y 1, y 2) (y 3, y 1 , y 2 , y 4) z 6 (y 3 , y 1 , y 2) z 5 (y 3, y 1, y 2) z 5 z 6 (y 1, y 1 , y 2 , y 4) z 6 26

Example continued. . . a, b z 1± a, b z 2 a z 3 a, b z 5+ b z 4+ b a z 6+ a, b 27

Summing Up • Examples of Kleene’s theorem part III (method 1) continued , Kleene’s theorem part III (method 2: Concatenation of FAs), Examples of Kleene’s theorem part III(method 2: concatenation FAs) continued, Kleene’s theorem part III (method 3: closure of an FA), examples of Kleene’s theorem part III(method 3: Closure of an FA) continued 28