Recap Lecture 12 z Examples of writing REs

Recap Lecture 12 z Examples of writing REs to the corresponding TGs, RE corresponding to TG accepting EVEN -EVEN language, Kleene’s theorem part III (method 1: union of FAs), examples of FAs corresponding to simple REs, example of Kleene’s theorem part III (method 1) continued 1

Note z It may be noted that in the previous example FA 1 contains two states while FA 2 contains three states. Hence the total number of possible combinations of states of FA 1 and FA 2, in sequence, will be six. For each combination the transitions for both a and b can be determined, but using the method in the example, number of states of FA 3 was reduced to five. 2

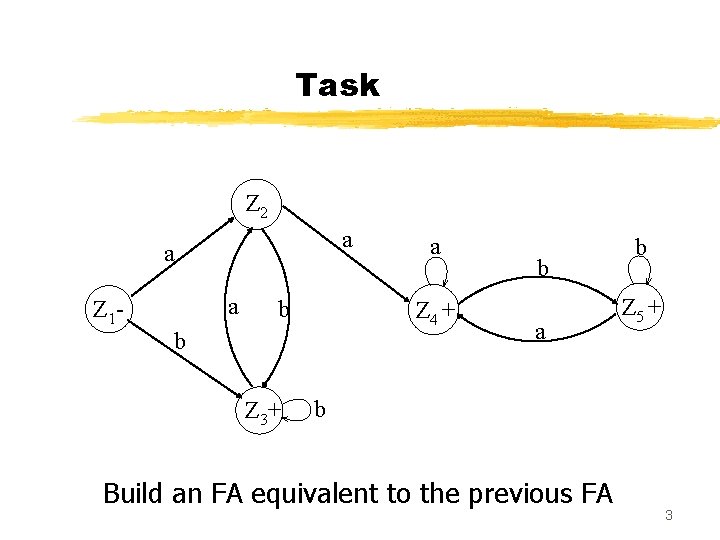
Task Z 2 a a a Z 1 - b Z 4 + b Z 3+ a b Z 5 + b Build an FA equivalent to the previous FA 3

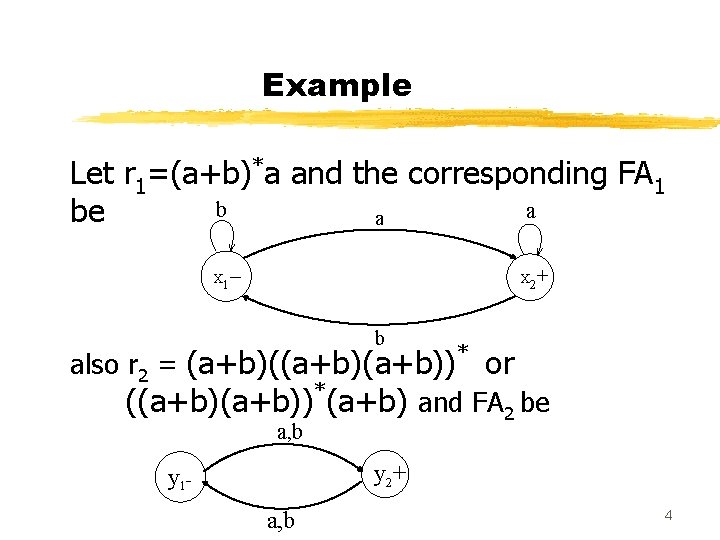
Example Let r 1=(a+b)*a and the corresponding FA 1 b a be a – + X 1 X 2 b also r 2 = (a+b)(a+b))* or ((a+b))*(a+b) and FA 2 be a, b y 2+ y 1 a, b 4

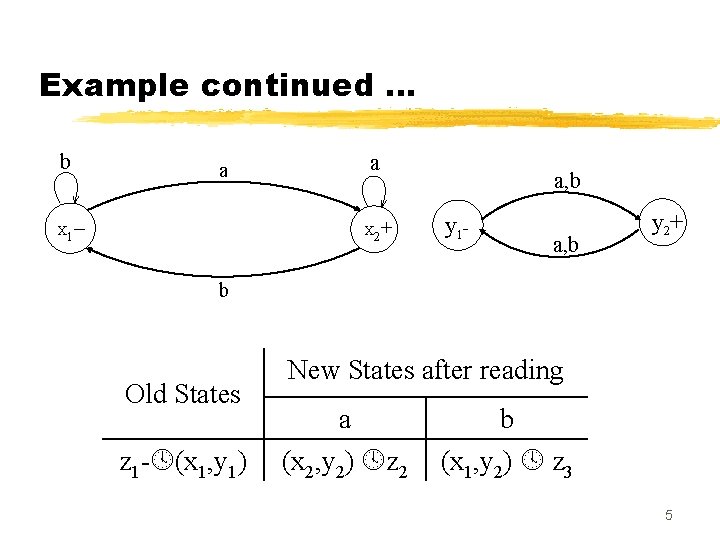
Example continued … b a – a a, b + X 1 X 2 y 1 - a, b y 2+ b Old States z 1 - (x 1, y 1) New States after reading a (x 2, y 2) z 2 b (x 1, y 2) z 3 5

Example continued … Old States New States after reading a z 2+ (x 2, y 2) (x 2, y 1) z 4 z 3+ (x 1, y 2) (x 2, y 1) z 4+ (x 2, y 1) (x 2, y 2) z 2 b (x 1, y 1) z 1 (x 1, y 2) z 3 6

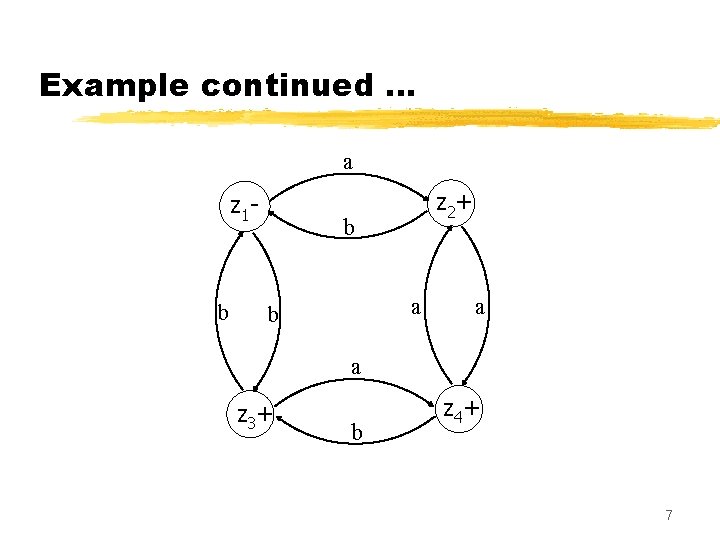
Example continued … a z 1 - b z 2 + b a a z 3 + b z 4 + 7

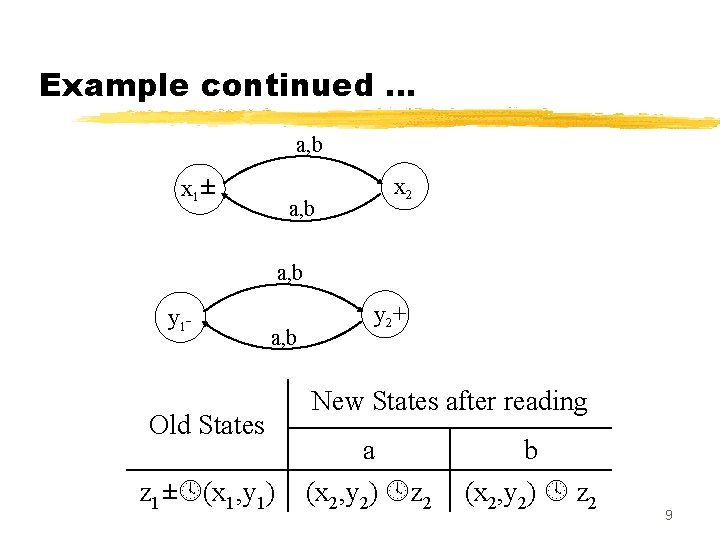
Example Let r 1=((a+b))* and the corresponding FA 1 be a, b x 1± a, b x 2 also r 2 = (a+b)(a+b))* or ((a+b))*(a+b) and FA 2 be a, b y 2+ y 1 a, b 8

Example continued … a, b x 1± a, b x 2 a, b y 1 - a, b Old States z 1± (x 1, y 1) y 2+ New States after reading a (x 2, y 2) z 2 b (x 2, y 2) z 2 9

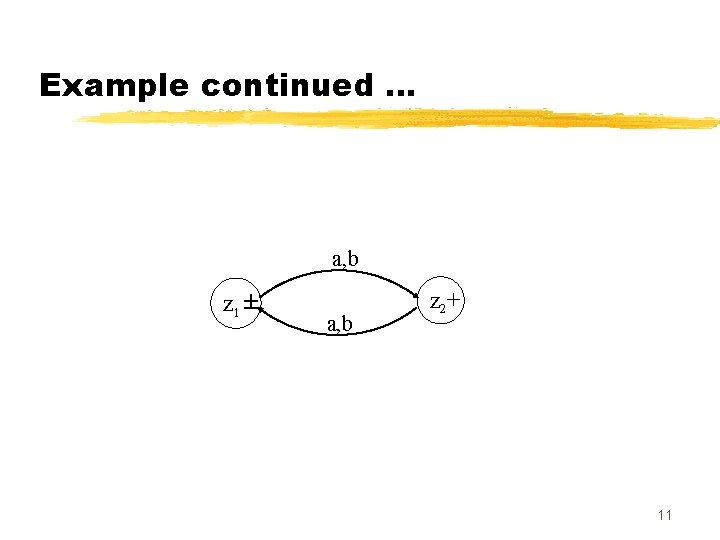
Example continued … Old States z 2+ (x 2, y 2) New States after reading a (x 1, y 1) z 1 b (x 1, y 1) z 1 10

Example continued … a, b z 1 ± a, b z 2+ 11

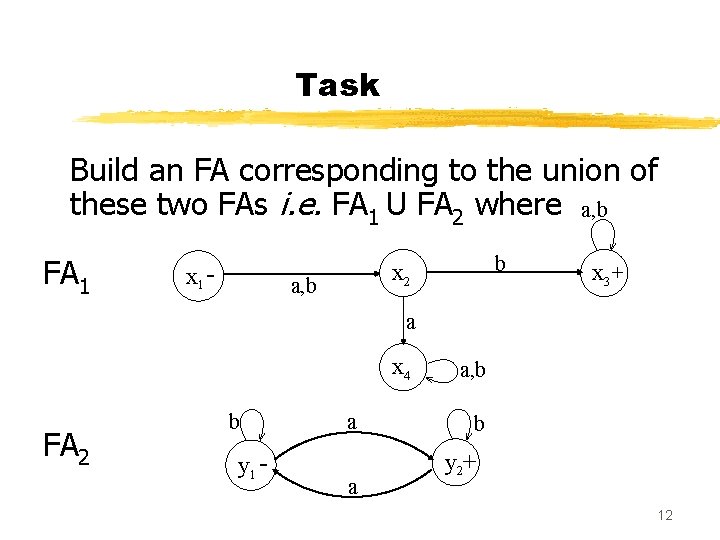
Task Build an FA corresponding to the union of these two FAs i. e. FA 1 U FA 2 where a, b FA 1 x 1 - b x 2 a, b x 3 + a x 4 FA 2 b y 1 - a a a, b b y 2+ 12

Kleene’s Theorem Part III Continued … z. Method 2 (Concatenation of two FAs): Using the FAs corresponding to r 1 and r 2, an FA can be built, corresponding to r 1 r 2. This method can be developed considering the following examples 13

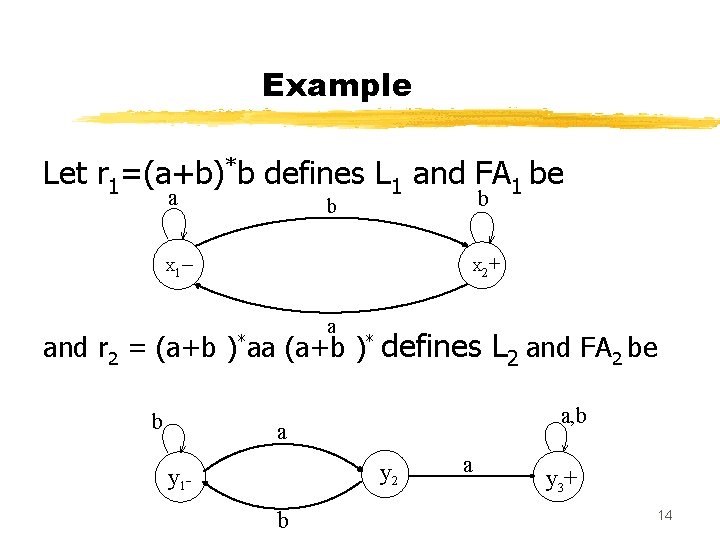
Example Let r 1=(a+b)*b defines L 1 and FA 1 be a b b – + X 1 X 2 a and r 2 = (a+b )*aa (a+b )* defines L 2 and FA 2 be b a, b a y 2 y 1 b a y 3+ 14

Concatenation of two FAs Continued … Let FA 3 be an FA corresponding to r 1 r 2, then the initial state of FA 3 must correspond to the initial state of FA 1 and the final state of FA 3 must correspond to the final state of FA 2. Since the language corresponding to r 1 r 2 is the concatenation of corresponding languages L 1 and L 2, consists of the strings obtained, concatenating the strings of L 1 to those of L 2 , therefore the moment a final state of first FA is entered, the possibility of the initial state of second FA will be included as well. 15

Concatenation of two FAs Continued … Since, in general, FA 3 will be different from both FA 1 and FA 2, so the labels of the states of FA 3 may be supposed to be z 1, z 2, z 3, …, where z 1 stands for the initial state. Since z 1 corresponds to the states x 1, so there will be two transitions separately for each letter read at z 1. It will give two possibilities of states which correspond to either z 1 or different from z 1. This process may be expressed in the following transition table for all possible states of FA 3 16

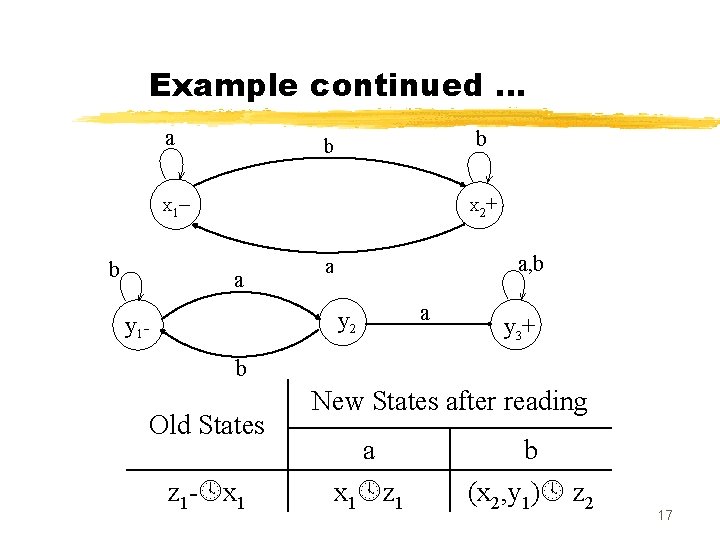
Example continued … a b b – + X 1 b X 2 a a, b a y 2 y 1 - a y 3+ b Old States z 1 - x 1 New States after reading a x 1 z 1 b (x 2, y 1) z 2 17

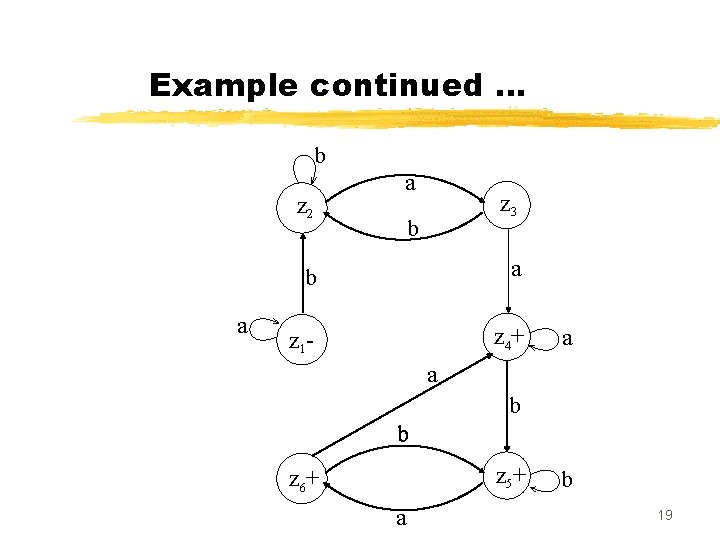
Example continued … Old States New States after reading a b z 2 (x 2, y 1) (x 1, y 2) z 3 (x 2, y 1) z 2 z 3 (x 1, y 2) (x 1, y 3) z 4 (x 2, y 1) z 2 z 4+ (x 1, y 3) z 4 (x 2, y 1, y 3) z 5+ (x 2, y 1, y 3) (x 1, y 2 , y 3) z 6 (x 2, y 1, y 3) z 5 z 6+ (x 1, y 2, y 3) (x 2 , y 1, y 3) z 5 (x 1, y 3) z 4 18

Example continued … b z 2 a a z 3 b b a z 1 - z 4+ a a b b z 5+ z 6+ a b 19

Summing Up z Examples of Kleene’s theorem part III (method 1) continued , Kleene’s theorem part III (method 2: Concatenation of FAs), z Example of Kleene’s theorem part III (method 2 : Concatenation of FAs) 20