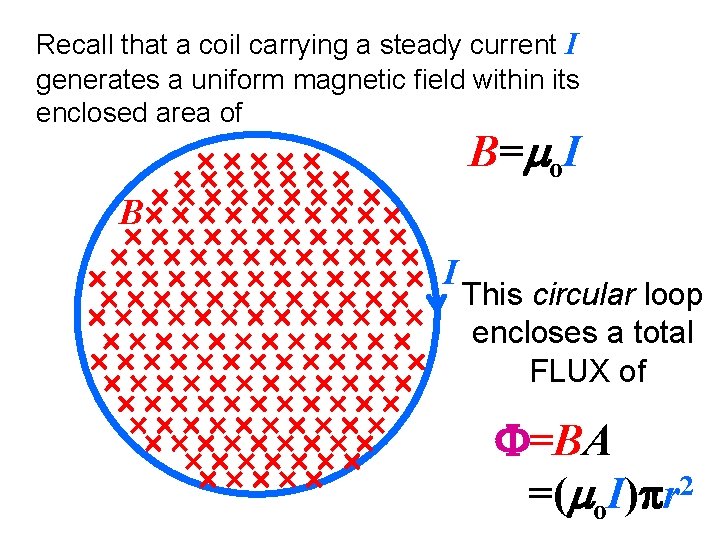
Recall that a coil carrying a steady current



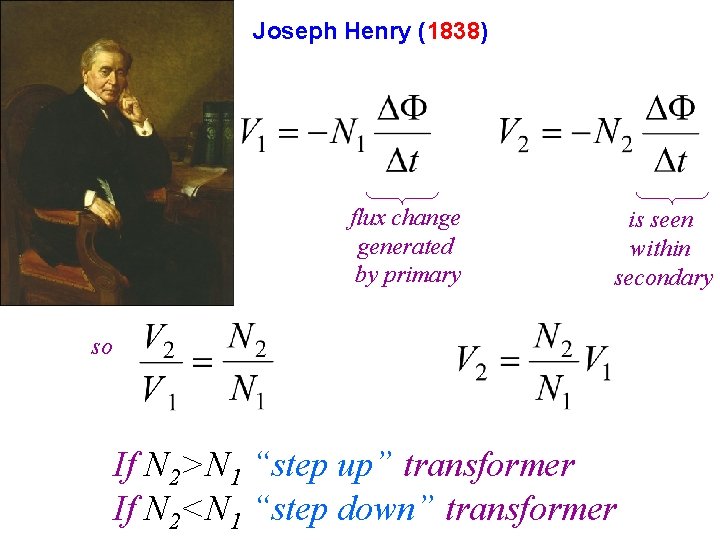



- Slides: 23

Recall that a coil carrying a steady current I generates a uniform magnetic field within its enclosed area of B=mo. I B I This circular loop encloses a total FLUX of =BA 2 =(mo. I)pr

Michael Faraday (1831)

A wire coiled into two loops carries a current, I. It faces a single independent loop enclosing the same cross-sectional area. The flux through the secondary (red) loop must be Here assume =BA 2 =(mo. I)pr 1) =(mo. I)pr 2. 2) ½. 3) 2. 4) 3. 5) zero.

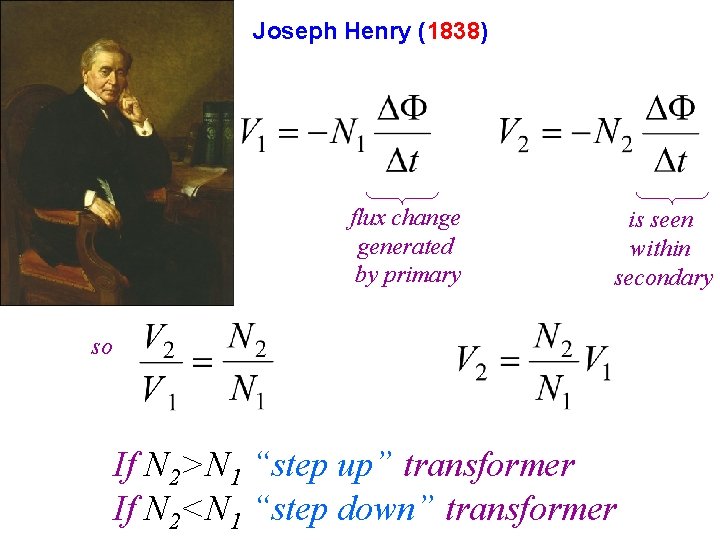
Joseph Henry (1838) flux change generated by primary is seen within secondary so If N 2>N 1 “step up” transformer If N 2<N 1 “step down” transformer

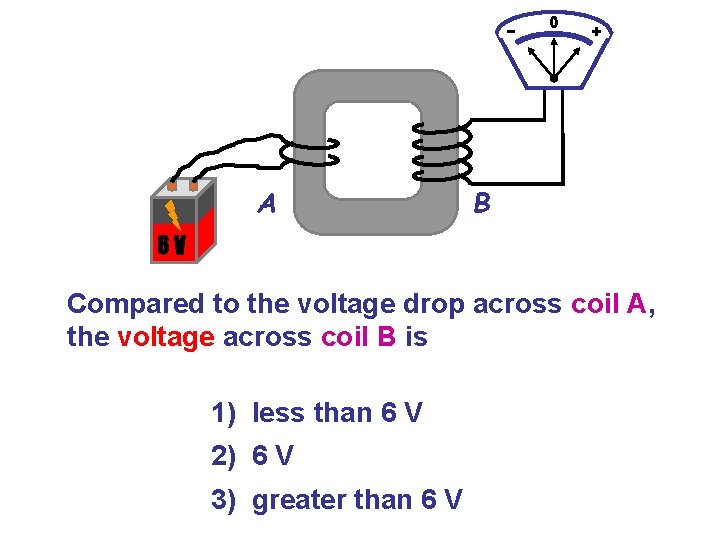
A B 6 V Compared to the voltage drop across coil A, the voltage across coil B is 1) less than 6 V 2) 6 V 3) greater than 6 V

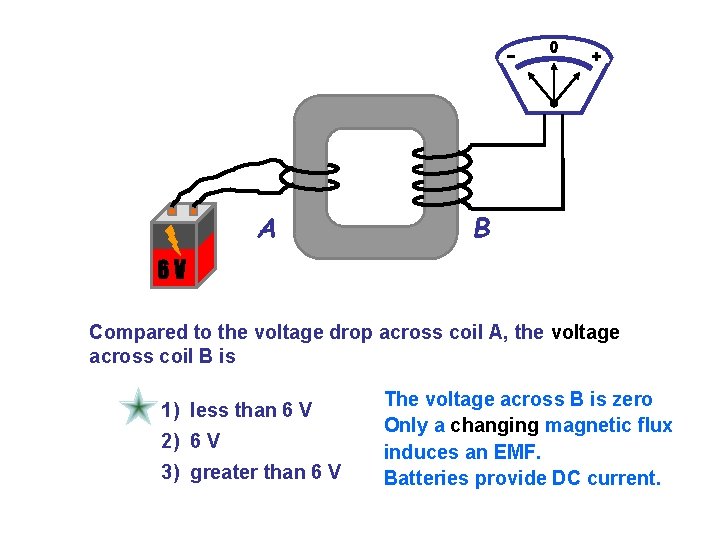
A B 6 V Compared to the voltage drop across coil A, the voltage across coil B is 1) less than 6 V 2) 6 V 3) greater than 6 V The voltage across B is zero Only a changing magnetic flux induces an EMF. Batteries provide DC current.

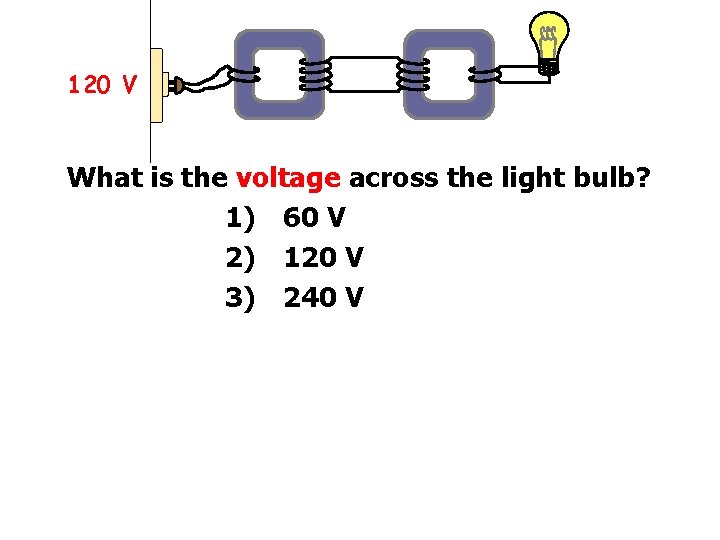
120 V What is the voltage across the light bulb? 1) 60 V 2) 120 V 3) 240 V

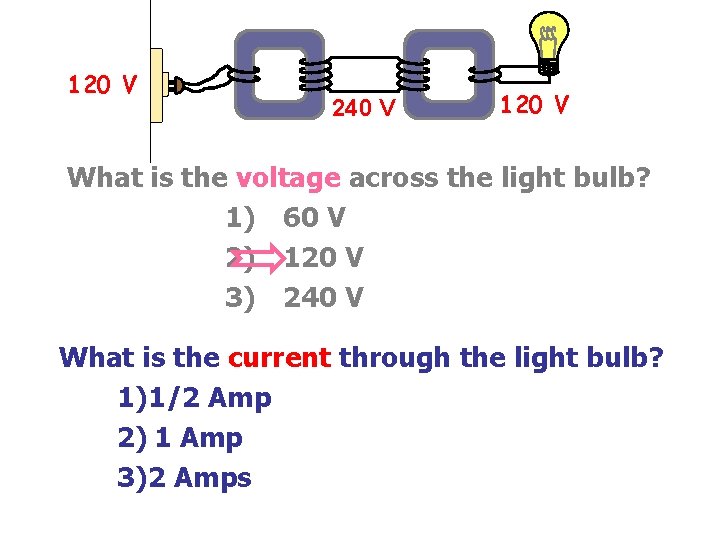
120 V 240 V 120 V What is the voltage across the light bulb? 1) 60 V 2) 120 V 3) 240 V What is the current through the light bulb? 1)1/2 Amp 2) 1 Amp 3)2 Amps

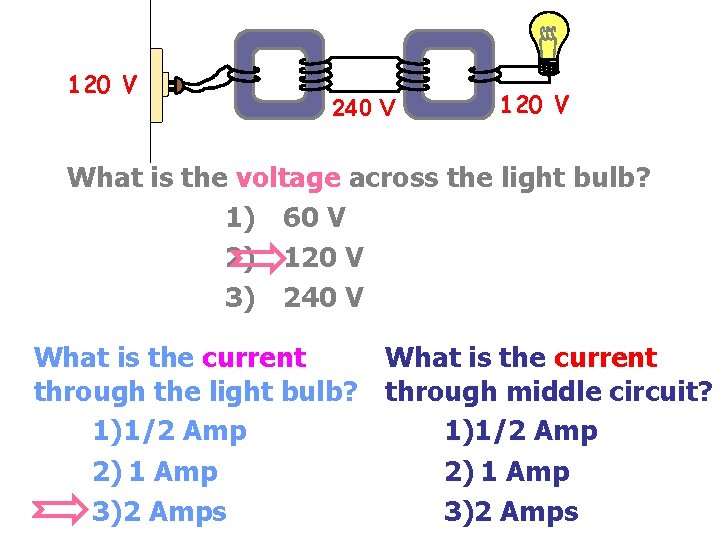
120 V 240 V 120 V What is the voltage across the light bulb? 1) 60 V 2) 120 V 3) 240 V What is the current through the light bulb? through middle circuit? 1)1/2 Amp 2) 1 Amp 3)2 Amps

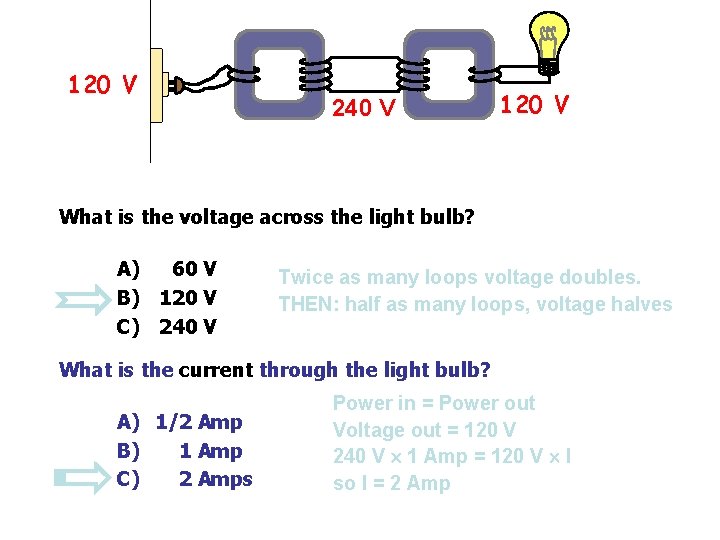
120 V 240 V 120 V What is the voltage across the light bulb? A) 60 V B) 120 V C) 240 V Twice as many loops voltage doubles. THEN: half as many loops, voltage halves What is the current through the light bulb? A) 1/2 Amp B) 1 Amp C) 2 Amps Power in = Power out Voltage out = 120 V 240 V 1 Amp = 120 V I so I = 2 Amp

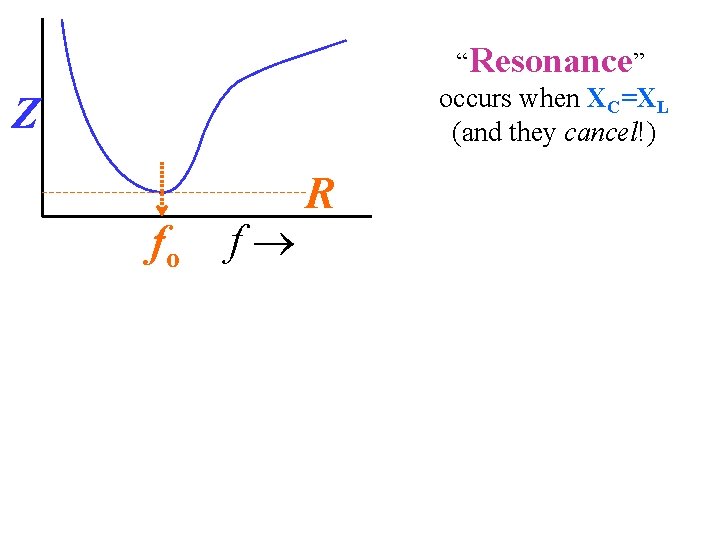
“Resonance” occurs when XC=XL (and they cancel!) Z fo f R

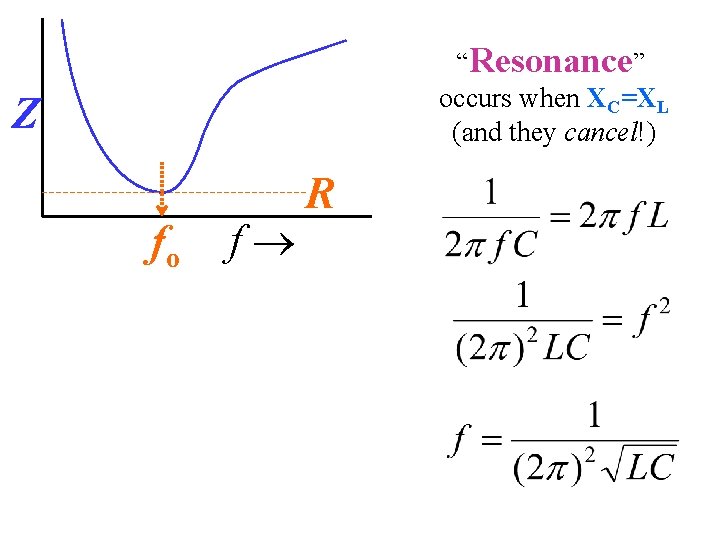
“Resonance” occurs when XC=XL (and they cancel!) Z fo f R

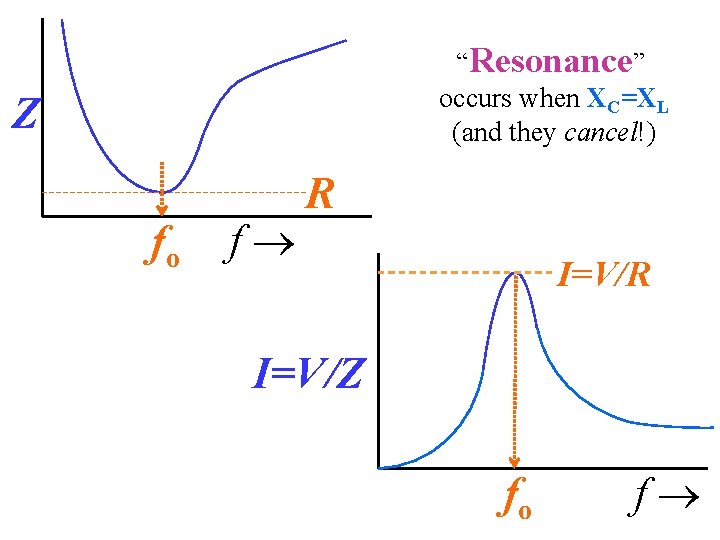
“Resonance” occurs when XC=XL (and they cancel!) Z fo f R I=V/Z fo f

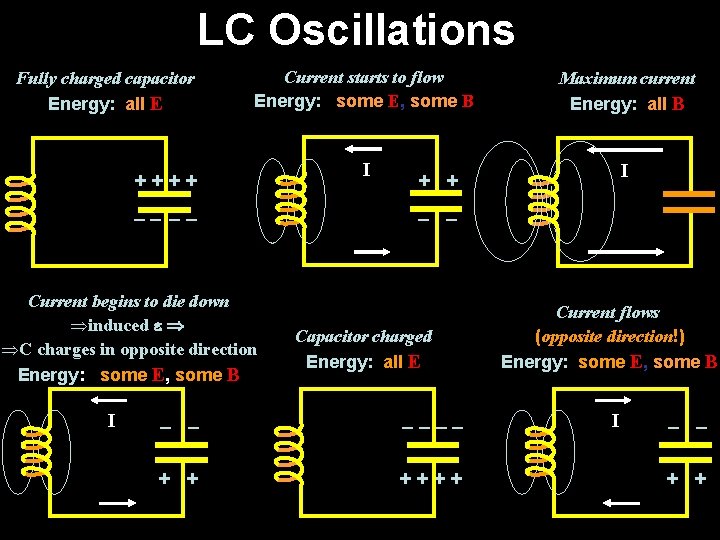
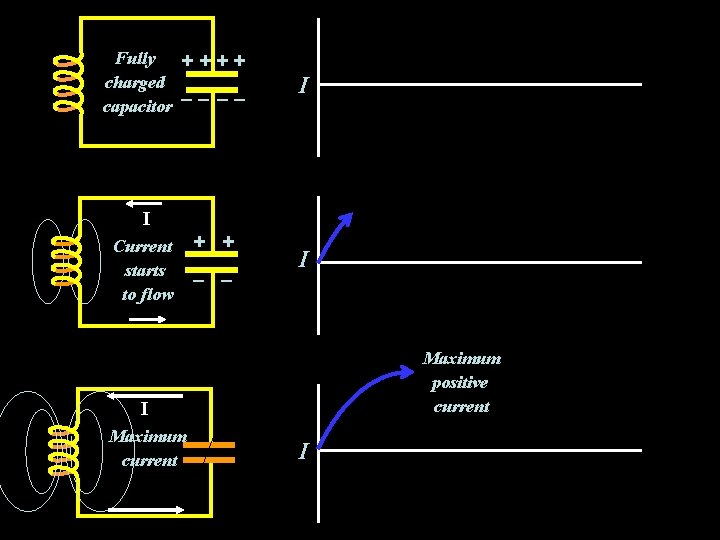
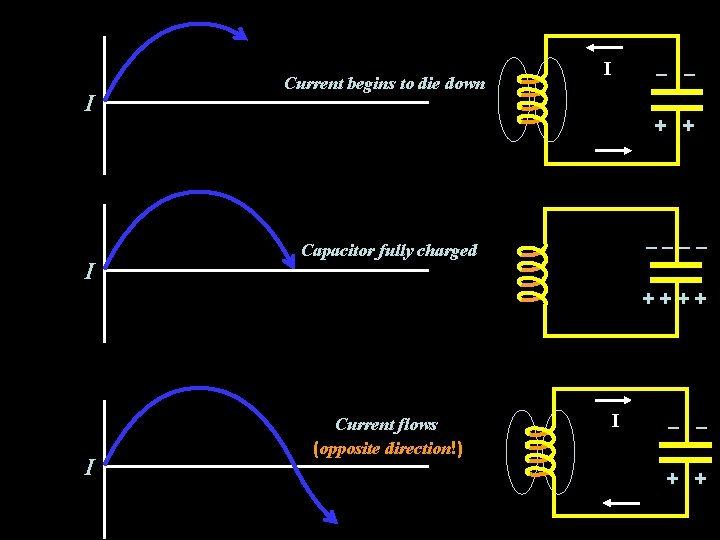
LC Oscillations Current starts to flow Energy: some E, some B Maximum current Energy: all B I I – – + + I Capacitor charged Energy: all E ++++ Current begins to die down Þinduced ÞC charges in opposite direction Energy: some E, some B – – Current flows (opposite direction!) Energy: some E, some B I + + –– –– + + –––– ++++ – – Fully charged capacitor Energy: all E

Fully + + charged capacitor – – I I Current starts to flow + + – – I Maximum positive current I Maximum current I

+ + –––– I – – I Current begins to die down I Capacitor fully charged ++++ + + I – – I Current flows (opposite direction!)

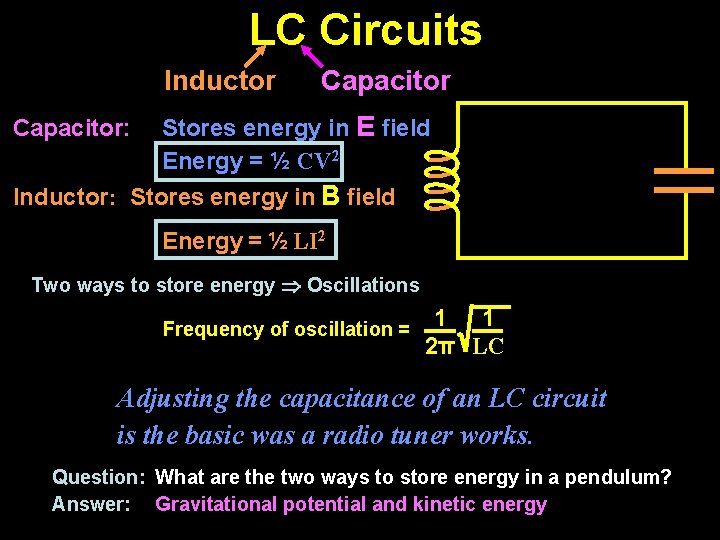
LC Circuits Inductor Capacitor: Capacitor Stores energy in E field Energy = ½ CV 2 Inductor: Stores energy in B field Energy = ½ LI 2 Two ways to store energy Oscillations Frequency of oscillation = 1 1 2π LC Adjusting the capacitance of an LC circuit is the basic was a radio tuner works. Question: What are the two ways to store energy in a pendulum? Answer: Gravitational potential and kinetic energy

http: //micro. magnet. fsu. edu/electromag/java/varcapacitor/

A radio is tuned to 141 MHz. If the tuner is to be set for 100 MHz, the capacitance of the LC circuit in the radio must be A) quadrupled B) doubled C) not changed D) halved E) quartered

A radio is tuned to 141 MHz. If the tuner is to be set for 100 MHz, the capacitance of the LC circuit in the radio must be A) quadrupled B) doubled C) not changed D) halved E) quartered f= 1 1 2π LC C 2 C then f (1/ 2) f 2 = 1. 41 141 MHz / 1. 41 = 100 MHz

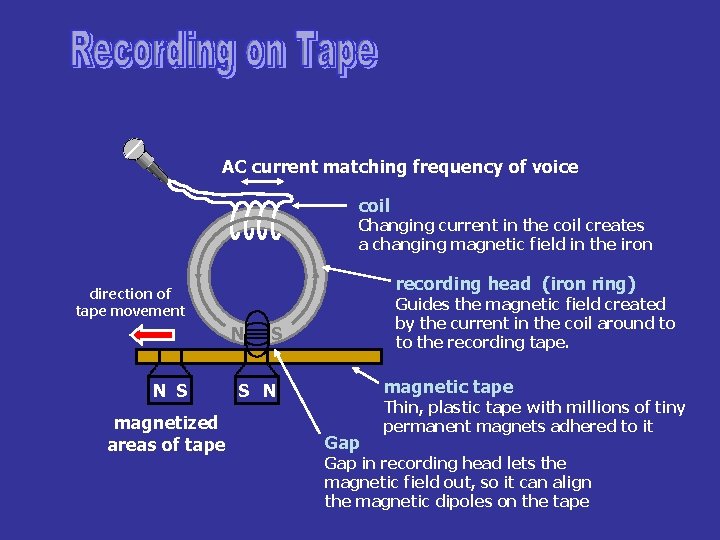
changing current produces changing B field AC current matching frequency of voice coil Changing current in the coil creates a changing magnetic field in the iron recording head (iron ring) direction of tape movement N N S magnetized areas of tape Guides the magnetic field created by the current in the coil around to to the recording tape. S magnetic tape S N Gap Thin, plastic tape with millions of tiny permanent magnets adhered to it Gap in recording head lets the magnetic field out, so it can align the magnetic dipoles on the tape

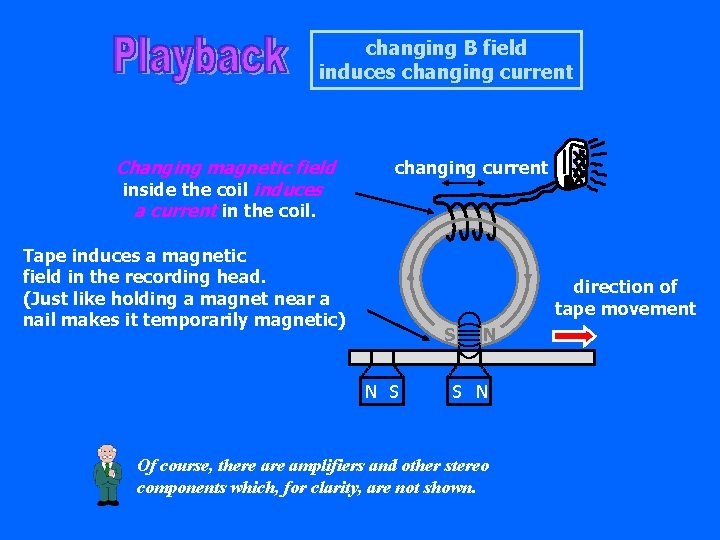
changing B field induces changing current Changing magnetic field inside the coil induces a current in the coil. changing current Tape induces a magnetic field in the recording head. (Just like holding a magnet near a nail makes it temporarily magnetic) direction of tape movement S N S N Of course, there amplifiers and other stereo components which, for clarity, are not shown.