Reasoning with Rules SWRL as Example Jan Pettersen

Reasoning with Rules SWRL as Example Jan Pettersen Nytun, UIA 1

JPN, Ui. A 2

What is a rule? • Consist of premise and a conclusion. • Meaning: In any situation where the premise applies the conclusion must also hold. premise conclusion JPN, Ui. A 3

Agenda v Different Types of Reasoning • Inductive reasoning • Deductive reasoning • Abductive reasoning v v v Why rules? The Semantic Web Rule Language (SWRL) SWRL Types of Atoms SWRL Example SWRL Exercise 4

Inductive Reasoning From Wikipedia, the free encyclopedia …the premises are viewed as supplying strong evidence for the truth of the conclusion. … conclusion of a deductive argument is certain, the truth of the conclusion of an inductive argument is probable, based upon the evidence given. … premise conclusion Not as strong as for deductive reasoning JPN, Ui. A 5

S P O Inductive Reasoning From Wikipedia, the free encyclopedia …the premises of an inductive logical argument indicate some degree of support for the conclusion but do not entail it. . . derives general principles from specific observations based on observations premise conclusion Likely to be true JPN, Ui. A 6

Inductive Reasoning Example Many observations indicate that humans eventually dies, i. e. , humans are mortals. Human(x) Mortal(x) JPN, Ui. A 7

Deductive Reasoning also Called Deductive Logic, Logical Deduction From Wikipedia, the free encyclopedia • If all premises are true, and the rules of deductive logic are followed, then the conclusion reached is necessarily true. • In inductive reasoning, the conclusion is reached by generalizing or extrapolating from specific cases to general rules, i. e. , there is … uncertainty. • However, induction used in mathematical proofs is actually a form of deductive reasoning. JPN, Ui. A 8

Deductive Reasoning Example All men are mortal. Socrates is a man. ---------------Therefore, Socrates is mortal. JPN, Ui. A 9

Deductive Reasoning Example in First Order Predicate Logic All men are mortal. Socrates is a man. ---------------Therefore, Socrates is mortal. ∀x. Man(x) Mortal(x) -- All men are mortal Man(Socrates) -- Socrates is a man -------------------------Man(Socrates) Mortal(Socrates). -- Socrates is mortal JPN, Ui. A 10

From Wikipedia, the free encyclopedia JPN, Ui. A 11

[https: //explorable. com/inductive-reasoning] Theories have to be tested and hypotheses answered before the scientific community accepts them as truth. JPN, Ui. A 12

Abductive Reasoning From Wikipedia, the free encyclopedia Example: The grass is wet; if it rained last night, then it would be unsurprising that the grass is wet. Therefore, by abductive reasoning, the possibility that it rained last night is reasonable. Raind. Last. Night Grass. Is. Weet Some other process could have also resulted in a wet grass, such as sprinklers. Consequently, abducing that it rained last night from the observation of wet grass can lead to a false conclusion. Sprinkler. Was. On Grass. Is. Weet JPN, Ui. A 13

Abductive Reasoning Continues… • Inference to the best explanation. • Given a true conclusion and a rule, it attempts to select some possible premises that, if true also, can support the conclusion, though not uniquely. Raind. Last. Night Grass. Is. Weet Sprinkler. Was. On Grass. Is. Weet • Can be used to develop a hypothesis, which in turn can be tested by additional reasoning or data. JPN, Ui. A 14

Abductive Reasoning Example ref. : https: //www. quora. com/What-is-a-good-example-of-abductive-reasoning • The doctor hears her patients symptoms, including the regular shortness of breath on cold days and when exercising and abduces that the best explanation of these symptoms is that her patient is an asthma sufferer. • The scientist observes the test tube and sees the chemical turn purple. She abduces that eithere is potassium in the sample or her colleague is playing yet another prank on her. JPN, Ui. A 15

Agenda v Different Types of Reasoning • Inductive reasoning • Deductive reasoning • Abductive reasoning v v v Why rules? The Semantic Web Rule Language (SWRL) SWRL Types of Atoms SWRL Example SWRL Exercise 16

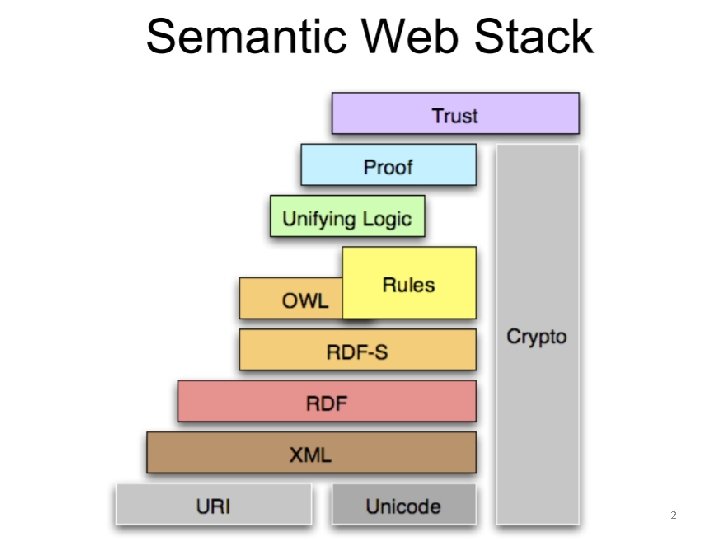
In some cases we need both Structure and Rules JPN, Ui. A 17

Example of rule using The Semantic Web Rule Language (SWRL): has. Parent(? x, ? parent) ∧ has. Brother(? parent, ? uncle) ⇒ has. Uncle(? x, ? uncle) • Some statements cannot be expressed in OWL. • Modeling constructs of OWL not always adequate or most desirable. Knowledge Representation, Part II, JPN, Ui. A 18

Agenda v Different Types of Reasoning • Inductive reasoning • Deductive reasoning • Abductive reasoning v v v Why rules? The Semantic Web Rule Language (SWRL) SWRL Types of Atoms SWRL Example SWRL Exercise 19

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ The Semantic Web Rule Language (SWRL) • An expressive OWL-based rule language. • SWRL allows users to write rules that can be expressed in terms of OWL concepts to provide more powerful deductive reasoning capabilities than OWL alone. JPN, Ui. A 20

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ SWRL Rule head body atom ^ atom. . → atom ^ atom body and head consist of positive conjunctions of atoms (only AND between atoms) Atom p(arg 1, arg 2, . . . argn) p is a predicate symbol; arg 1, arg 2, . . . , argn are the terms of the expression. JPN, Ui. A 21

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ All variables in SWRL are treated as universally quantified ( ), with their scope limited to a given rule. E. g. , given: has. Parent(? x, ? parent) ∧ has. Brother(? parent, ? uncle) ⇒ has. Uncle(? x, ? uncle) This rule applies for all ? x, all ? parent and all ? uncle. JPN, Ui. A 22

Agenda v Different Types of Reasoning • Inductive reasoning • Deductive reasoning • Abductive reasoning v v v Why rules? The Semantic Web Rule Language (SWRL) SWRL Types of Atoms SWRL Example SWRL Exercise 23

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ SWRL provides seven types of atoms: • • Class Atoms Individual Property atoms Data Valued Property atoms Different Individuals atoms Same Individual atoms Built-in atoms Data Range atoms JPN, Ui. A 24

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ Class Atom OWL named class or class expression and a single argument representing an OWL individual Examples: Person(? p) Man(Fred) Man(? p) -> Person(? p) JPN, Ui. A 25

Example of Class Expression (has. Child >= 1)(? x) -> Parent(? x) JPN, Ui. A 26

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ Individual Property Atom OWL object property and two arguments representing OWL individuals. Examples: has. Brother(? x, ? y) has. Sibling(Fred, ? y) Person(? p) ^ has. Sibling(? p, ? s) ^ Man(? s) -> has. Brother(? p, ? s) JPN, Ui. A 27

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ Data Valued Property OWL data property and two arguments, the first representing an OWL individual, and the second a data value. Examples: has. Age(? x, ? age) has. Height(Fred, ? h) has. Age(? x, 232) has. Name(? x, "Fred") Person(? p) ^ has. Car(? p, true) -> Driver(? p) Person(Fred) ^ has. Car(Fred, true) -> Driver(Fred) JPN, Ui. A 28

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ Different Individuals Atom Arguments representing OWL individuals. Examples: different. From(? x, ? y) different. From(Fred, Joe) Same Individual Atom Arguments representing OWL individuals. Examples: same. As(? x, ? y) same. As(Fred, Freddy) JPN, Ui. A 29

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ Data Range Atom A datatype name or a set of literals and a single argument representing a data value. Examples: xsd: int(? x) [3, 4, 5](? x) ? x is a variable representing a data value. JPN, Ui. A 30

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ Built-In Atom SWRL support user-defined built-ins. A built-in is a predicate that takes one or more arguments and evaluates to true if the arguments satisfy the predicate. SWRL contained many built-ins. Example - Person with an age of greater than 17 is an adult is: : Person(? p) ^ has. Age(? p, ? age) ^ swrlb: greater. Than(? age, 17) -> Adult(? p) (swrlb is a namespace) JPN, Ui. A 31

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ A rule that uses a core SWRL string built-in to determine if a person's telephone number starts with the international access code "+" can be written as follows: Person(? p) ^ has. Number(? p, ? number) ^ swrlb: starts. With(? number, "+") has. International. Number(? p, true) JPN, Ui. A 32

Ref. : https: //github. com/protegeproject/swrlapi/wiki/SWRLLanguage. FAQ Rectangle(? r) ^ has. Width. In. Meters(? r, ? w) ^ has. Height. In. Meters(? r, ? h) ^ swrlb: multiply(? area. In. Square. Meters, ? w, ? h) has. Area. In. Square. Meters(? r, ? area. In. Square. Meters) JPN, Ui. A 33

Agenda v Different Types of Reasoning • Inductive reasoning • Deductive reasoning • Abductive reasoning v v v Why rules? The Semantic Web Rule Language (SWRL) SWRL Types of Atoms SWRL Example SWRL Exercise 34

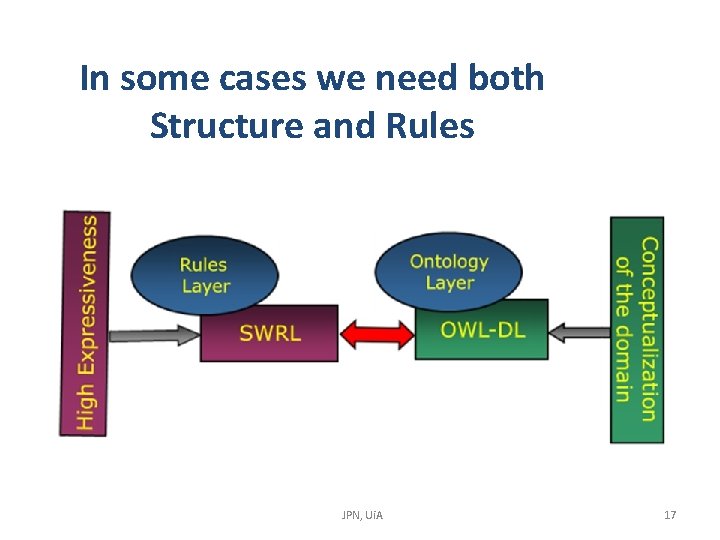
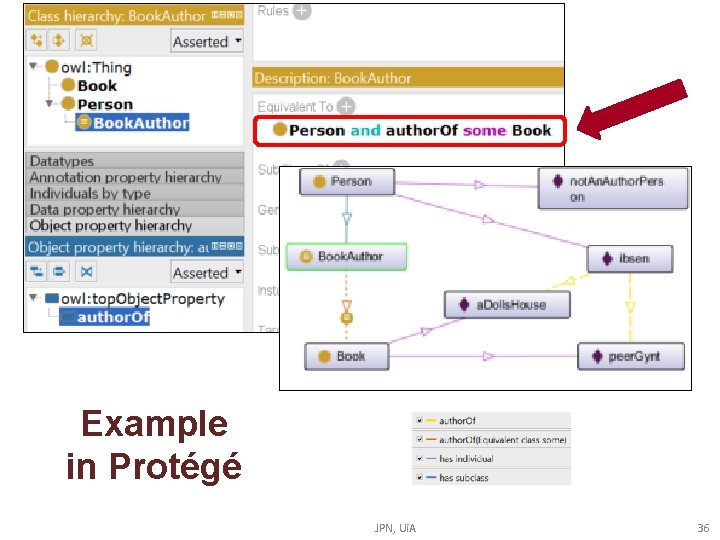
DL and SWRL has a big overlap Example: If a person is the author of a book then she is a (member of the class) book author. First Order Predicate Logic: ∀x. Person(x) ∧ ∃y. author. Of(x, y) ∧ Book(y) →Bookauthor(x) Description Logic: Person and author. Of some Book SWRL: Person(? x) ^ author. Of(? x, ? y) ^Book(? y) -> Book. Author(? x) JPN, Ui. A 35

Example in Protégé JPN, Ui. A 36

: author. Of rdf: type owl: Object. Property. : Book rdf: type owl: Class. : Person rdf: type owl: Class. Ontology Used : Book. Author rdf: type owl: Class ; owl: equivalent. Class [ owl: intersection. Of ( : Person [ rdf: type owl: Restriction ; owl: on. Property : author. Of ; owl: some. Values. From : Book ] ) ; rdf: type owl: Class ]. : a. Dolls. House rdf: type owl: Named. Individual , : Book. : ibsen rdf: type owl: Named. Individual , : Person ; : author. Of : a. Dolls. House , : peer. Gynt. : not. An. Author. Person rdf: type owl: Named. Individual , : Person. : peer. Gynt rdf: type owl: Named. Individual , : Book. JPN, Ui. A 37

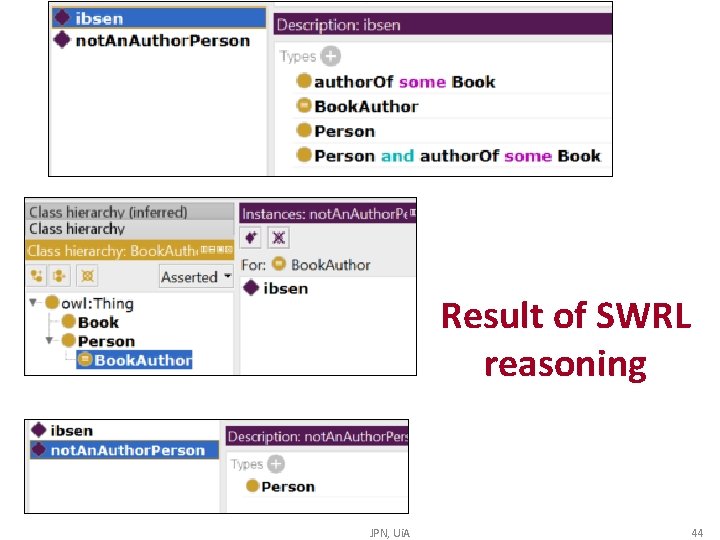
DL reasoner infer that ibsen is a book author JPN, Ui. A 38

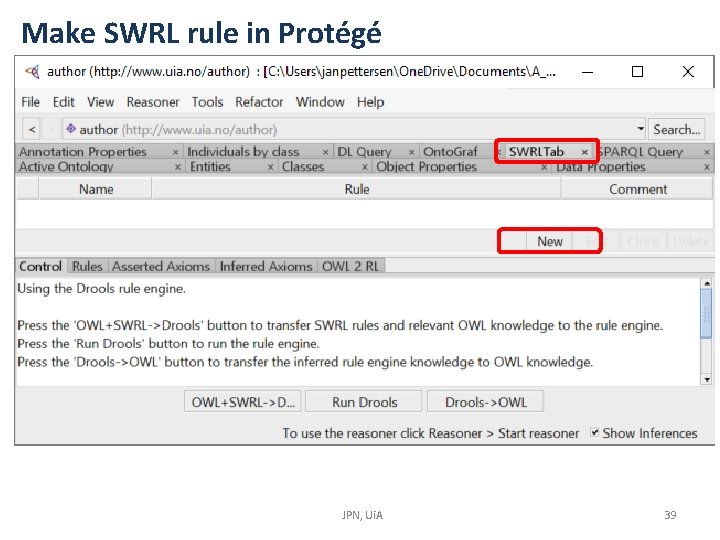
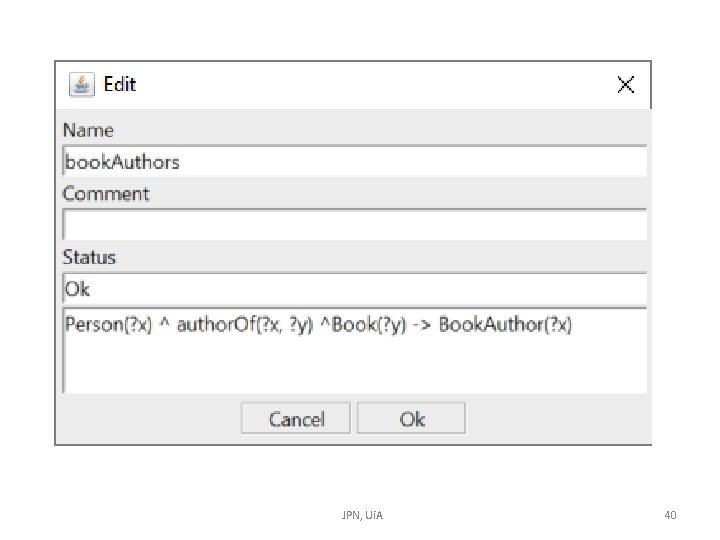
Make SWRL rule in Protégé JPN, Ui. A 39

JPN, Ui. A 40

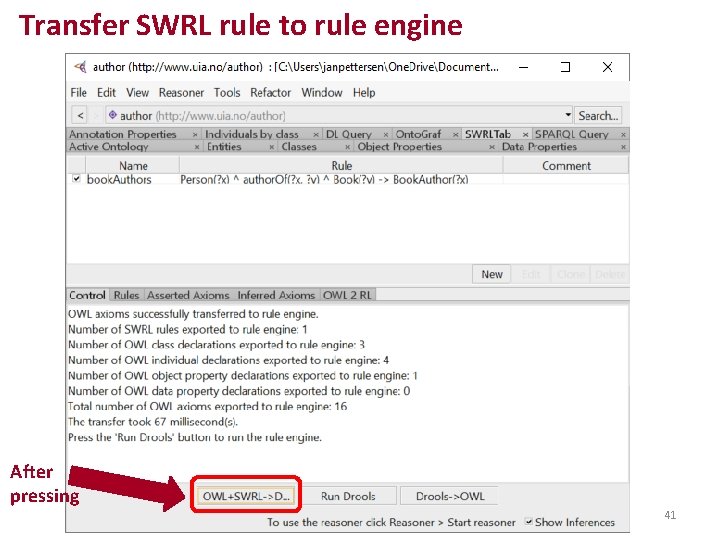
Transfer SWRL rule to rule engine After pressing JPN, Ui. A 41

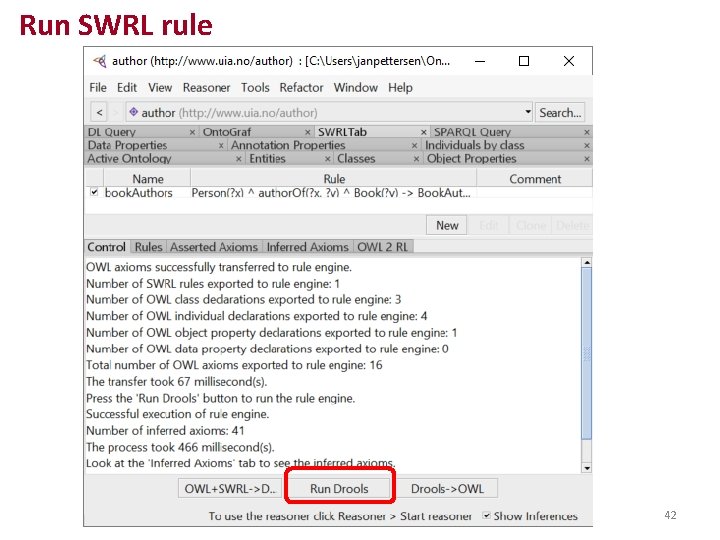
Run SWRL rule JPN, Ui. A 42

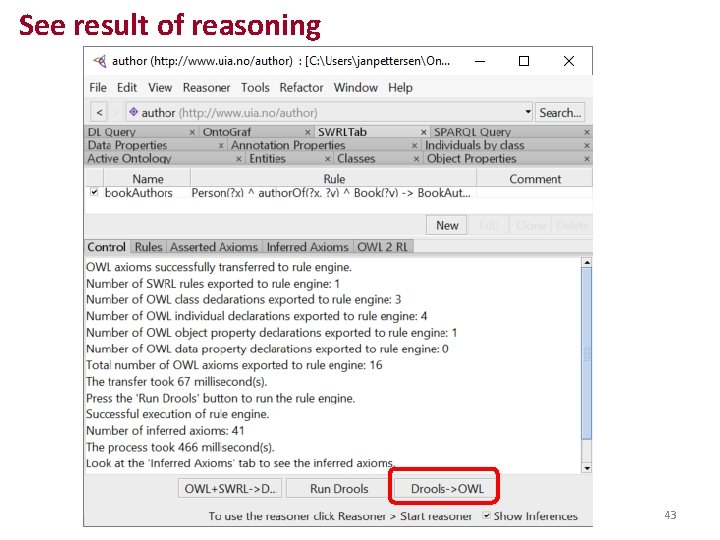
See result of reasoning JPN, Ui. A 43

Result of SWRL reasoning JPN, Ui. A 44

Agenda v Different Types of Reasoning • Inductive reasoning • Deductive reasoning • Abductive reasoning v v v Why rules? The Semantic Web Rule Language (SWRL) SWRL Types of Atoms SWRL Example SWRL Exercise 45

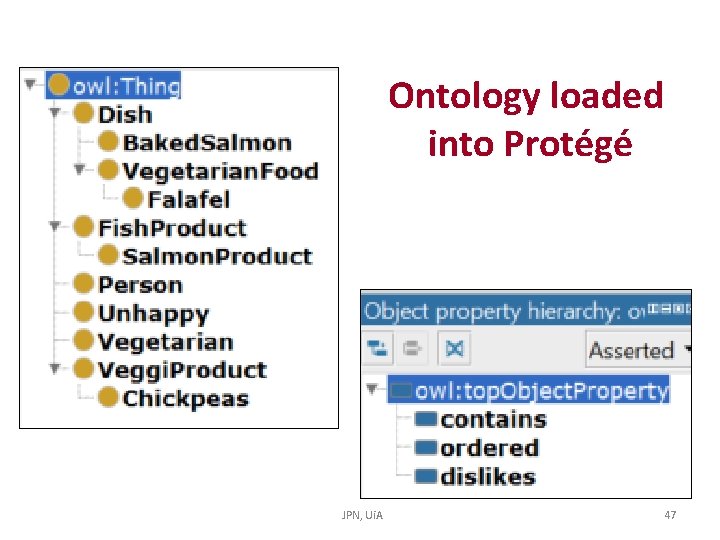
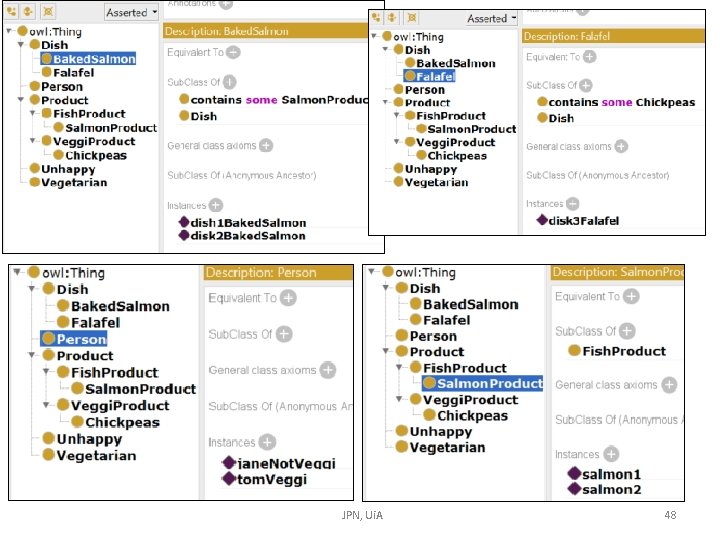
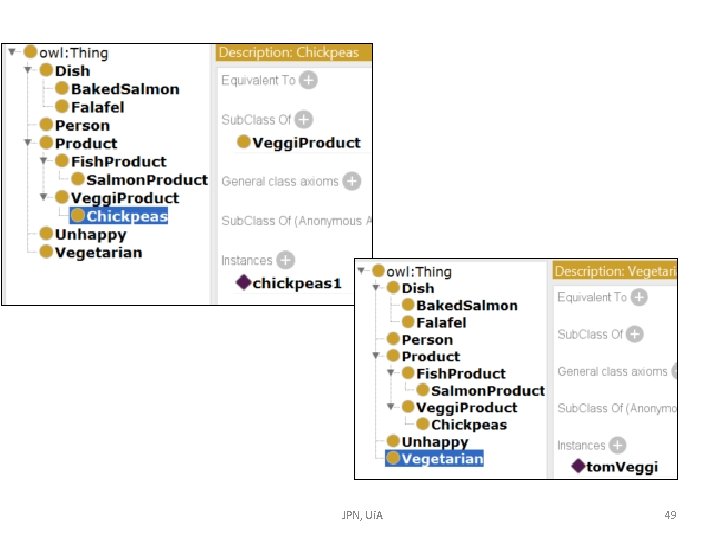
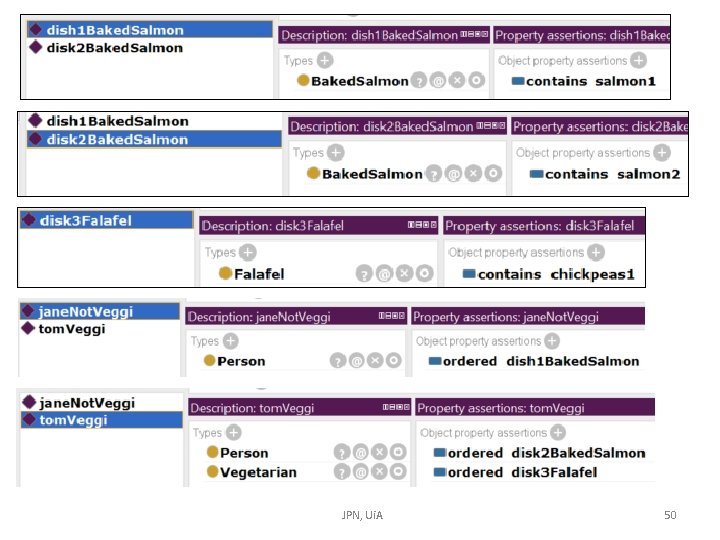
@prefix : <http: //www. uia. no/veggi#>. @prefix owl: <http: //www. w 3. org/2002/07/owl#>. @prefix rdf: <http: //www. w 3. org/1999/02/22 -rdf-syntax-ns#>. @prefix xml: <http: //www. w 3. org/XML/1998/namespace>. @prefix xsd: <http: //www. w 3. org/2001/XMLSchema#>. @prefix rdfs: <http: //www. w 3. org/2000/01/rdf-schema#>. @base <http: //www. uia. no/veggi> rdf: type owl: Ontology. ################################# # Object Properties ################################# ### http: //www. uia. no/veggi#contains : contains rdf: type owl: Object. Property. ### http: //www. uia. no/veggi#dislikes : dislikes rdf: type owl: Object. Property. ### http: //www. uia. no/veggi#ordered : ordered rdf: type owl: Object. Property. ################################# # Classes ################################# ### http: //www. uia. no/veggi#Baked. Salmon : Baked. Salmon rdf: type owl: Class ; rdfs: sub. Class. Of : Dish , [ rdf: type owl: Restriction ; owl: on. Property : contains ; owl: some. Values. From : Salmon. Product ]. ### http: //www. uia. no/veggi#Chickpeas : Chickpeas rdf: type owl: Class ; rdfs: sub. Class. Of : Veggi. Product. ### http: //www. uia. no/veggi#Dish : Dish rdf: type owl: Class. ### http: //www. uia. no/veggi#Falafel : Falafel rdf: type owl: Class ; rdfs: sub. Class. Of : Dish , [ rdf: type owl: Restriction ; owl: on. Property : contains ; owl: some. Values. From : Chickpeas ]. Exercise this ontology is given ### http: //www. uia. no/veggi#Fish. Product : Fish. Product rdf: type owl: Class ; rdfs: sub. Class. Of : Product. ### http: //www. uia. no/veggi#Person : Person rdf: type owl: Class. ### http: //www. uia. no/veggi#Product : Product rdf: type owl: Class. ### http: //www. uia. no/veggi#Salmon. Product : Salmon. Product rdf: type owl: Class ; rdfs: sub. Class. Of : Fish. Product. ### http: //www. uia. no/veggi#Unhappy : Unhappy rdf: type owl: Class. ### http: //www. uia. no/veggi#Vegetarian : Vegetarian rdf: type owl: Class. ### http: //www. uia. no/veggi#Veggi. Product : Veggi. Product rdf: type owl: Class ; rdfs: sub. Class. Of : Product. ################################# # Individuals ################################# ### http: //www. uia. no/veggi#chickpeas 1 : chickpeas 1 rdf: type owl: Named. Individual , : Chickpeas. ### http: //www. uia. no/veggi#dish 1 Baked. Salmon : dish 1 Baked. Salmon rdf: type owl: Named. Individual , : Baked. Salmon ; : contains : salmon 1. ### http: //www. uia. no/veggi#disk 2 Baked. Salmon : disk 2 Baked. Salmon rdf: type owl: Named. Individual , : Baked. Salmon ; : contains : salmon 2. ### http: //www. uia. no/veggi#disk 3 Falafel : disk 3 Falafel rdf: type owl: Named. Individual , : Falafel ; : contains : chickpeas 1. ### http: //www. uia. no/veggi#jane. Not. Veggi : jane. Not. Veggi rdf: type owl: Named. Individual , : Person ; : ordered : dish 1 Baked. Salmon. ### http: //www. uia. no/veggi#salmon 1 : salmon 1 rdf: type owl: Named. Individual , : Salmon. Product. ### http: //www. uia. no/veggi#salmon 2 : salmon 2 rdf: type owl: Named. Individual , : Salmon. Product. ### http: //www. uia. no/veggi#tom. Veggi : tom. Veggi rdf: type owl: Named. Individual , : Person , : Vegetarian ; : ordered : disk 2 Baked. Salmon , : disk 3 Falafel. ### Generated by the OWL API (version 4. 2. 5. 20160517 -0735) https: //github. com/owlcs/owlapi JPN, Ui. A 46

Ontology loaded into Protégé JPN, Ui. A 47

JPN, Ui. A 48

JPN, Ui. A 49

JPN, Ui. A 50

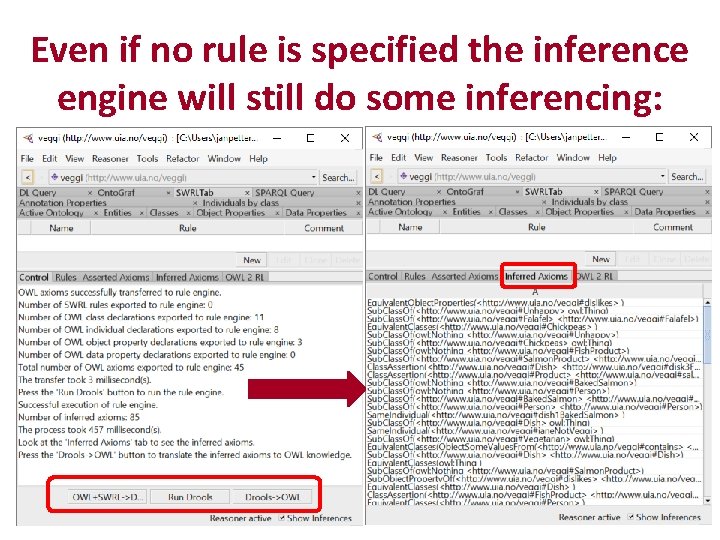
Even if no rule is specified the inference engine will still do some inferencing: JPN, Ui. A 51

Task 1: “Every vegetarian dislikes all fish products. ” In effect all individuals of type Vegetarian will dislike all individuals of type Fish. Product (and all its subclasses). E. g. : JPN, Ui. A 52

Task 1 Solution: (1)“Every vegetarian dislikes all fish products. ” Vegetarian(? x) ^ Fish. Product(? y) -> dislikes(? x, ? y) JPN, Ui. A 53

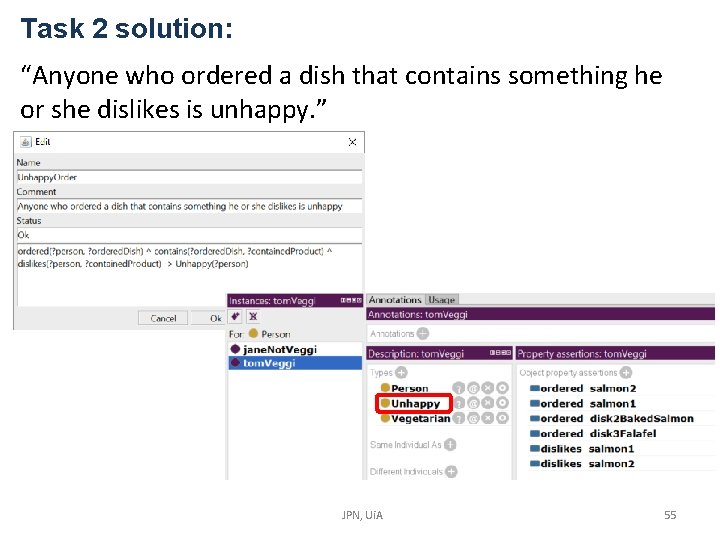
Task 2: “Anyone who ordered a dish that contains something he or she dislikes is unhappy. ” JPN, Ui. A 54

Task 2 solution: “Anyone who ordered a dish that contains something he or she dislikes is unhappy. ” JPN, Ui. A 55

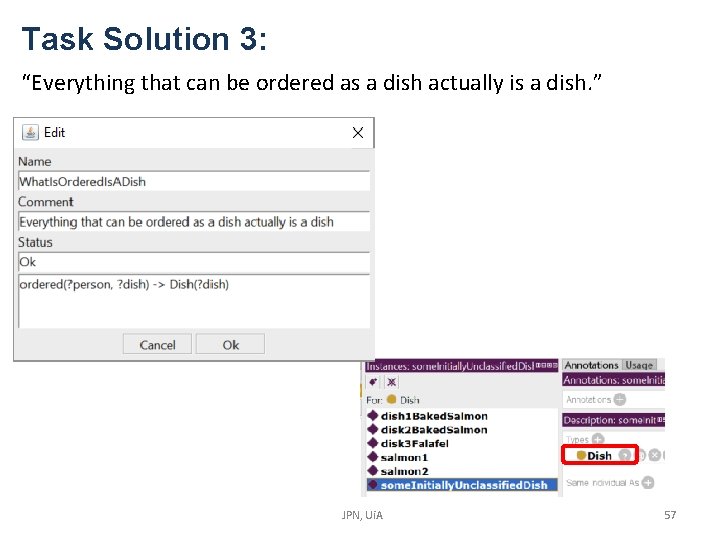
Task 3: “Everything that can be ordered as a dish actually is a dish. ” Add the following to test: JPN, Ui. A 56

Task Solution 3: “Everything that can be ordered as a dish actually is a dish. ” JPN, Ui. A 57

References Foundations of Semantic Web Technologies, Pascal Hitzler, Markus Krötzsch, Sebastian Rudolph, Chapman & Hall/CRC, 2009 http: //www. powershow. com/view 4/5 a 7 f 2 a. OGRl. M/SWRL_Semantic_Web_Rule_Language_powerpoint_ppt_presentation Help SWRL Protégé 5: https: //github. com/protegeproject/swrlapi/wiki Jan Pettersen Nytun, Ui. A, page 58