Reasoning Under Uncertainty Artificial Intelligence CMSC 25000 February

Reasoning Under Uncertainty Artificial Intelligence CMSC 25000 February 6, 2003

Agenda • Motivation – Reasoning with uncertainty • Medical Informatics • Probability and Bayes’ Rule – Bayesian Networks – Noisy-Or • Decision Trees and Rationality • Conclusions

Uncertainty • Search and Planning Agents – Assume fully observable, deterministic, static • Real World: – “Ignorance & Laziness” – Partially observable, stochastic – Can't be sure of success, agent will maximize

Motivation • Uncertainty in medical diagnosis – Diseases produce symptoms – In diagnosis, observed symptoms => disease ID – Uncertainties • Symptoms may not occur • Symptoms may not be reported • Diagnostic tests not perfect – False positive, false negative • How do we estimate confidence?

Motivation II • Uncertainty in medical decision-making – Physicians, patients must decide on treatments – Treatments may not be successful – Treatments may have unpleasant side effects • Choosing treatments – Weigh risks of adverse outcomes • People are BAD at reasoning intuitively about probabilities – Provide systematic analysis

Probabilities Model Uncertainty • The World - Features – Random variables – Feature values • States of the world – Assignments of values to variables – Exponential in # of variables – possible states

Probabilities of World States • : Joint probability of assignments – States are distinct and exhaustive • Typically care about SUBSET of assignments – aka “Circumstance” – Exponential in # of don’t cares

A Simpler World • 2^n world states = Maximum entropy – Know nothing about the world • Many variables independent – P(strep, ebola) = P(strep)P(ebola) • Conditionally independent – Depend on same factors but not on each other – P(fever, cough|flu) = P(fever|flu)P(cough|flu)

Probabilistic Diagnosis • Question: – How likely is a patient to have a disease if they have the symptoms? • Probabilistic Model: Bayes’ Rule • P(D|S) = P(S|D)P(D)/P(S) – Where • P(S|D) : Probability of symptom given disease • P(D): Prior probability of having disease • P(S): Prior probability of having symptom

Modeling (In)dependence • Bayesian network – Nodes = Variables – Arcs = Child depends on parent(s) • No arcs = independent (0 incoming: only a priori) • Parents of X = • For each X need

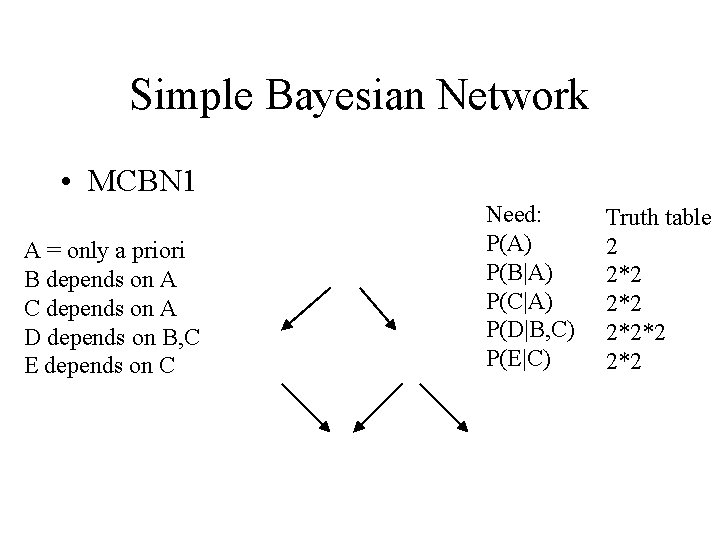
Simple Bayesian Network • MCBN 1 A = only a priori B depends on A C depends on A D depends on B, C E depends on C Need: P(A) P(B|A) P(C|A) P(D|B, C) P(E|C) Truth table 2 2*2 2*2*2

Simplifying with Noisy-OR • How many computations? – p = # parents; k = # values for variable – (k-1)k^p – Very expensive! 10 binary parents=2^10=1024 • Reduce computation by simplifying model – Treat each parent as possible independent cause – Only 11 computations • 10 causal probabilities + “leak” probability – “Some other cause”

Noisy-OR Example Pn(b|a) = 1 -(1 -ca)(1 -L) Pn(b|a) = 1 -(1 -L) = l = 0. 5 Pn(b|a) = (1 -L) P(B|A) b b a 0. 6 0. 4 a 0. 5 Pn(b|a) = 1 -(1 -ca)(1 -L)=0. 6 (1 -ca)(1 -L)=0. 4 (1 -ca) =0. 4/(1 -L) =0. 4/0. 5=0. 8 ca = 0. 2

Noisy-OR Example II Full model: P(c|ab)P(c|ab) & neg Noisy-Or: ca, cb, L Pn(c|ab) = 1 -(1 -ca)(1 -cb)(1 -L) Pn(c|ab) = 1 -(1 -ca)(1 -L) Pn(c|ab) = 1 -(1 -L) = l = 0. 3 Pn(c|b)=Pn(c|ab)Pn(a)+Pn(c|ab)P(a) 1 -0. 7=(1 -ca)(1 -cb)(1 -L)0. 1+(1 -cb)(1 -L)0. 9 0. 3=0. 5(1 -cb)0. 07+(1 -cb)0. 7*0. 9 =0. 035(1 -cb)+0. 63(1 -cb)=0. 665(1 -cb) 0. 55=cb Assume: P(a)=0. 1 P(b)=0. 05 P(c|ab)=0. 3 ca= 0. 5 P(c|b) = 0. 7

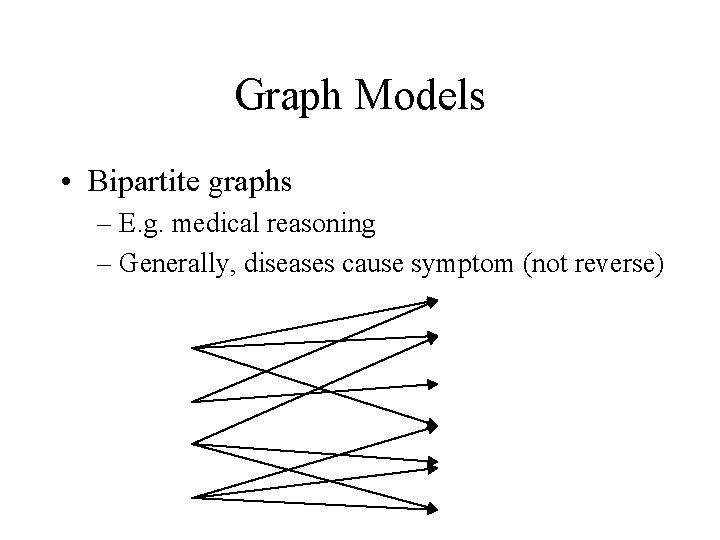
Graph Models • Bipartite graphs – E. g. medical reasoning – Generally, diseases cause symptom (not reverse)

Topologies • Generally more complex – Polytree: One path between any two nodes • General Bayes Nets – Graphs with undirected cycles • No directed cycles - can’t be own cause • Issue: Automatic net acquisition – Update probabilities by observing data – Learn topology: use statistical evidence of indep, heuristic search to find most probable structure

Decision Making • Design model of rational decision making – Maximize expected value among alternatives • Uncertainty from – Outcomes of actions – Choices taken • To maximize outcome – Select maximum over choices – Weighted average value of chance outcomes

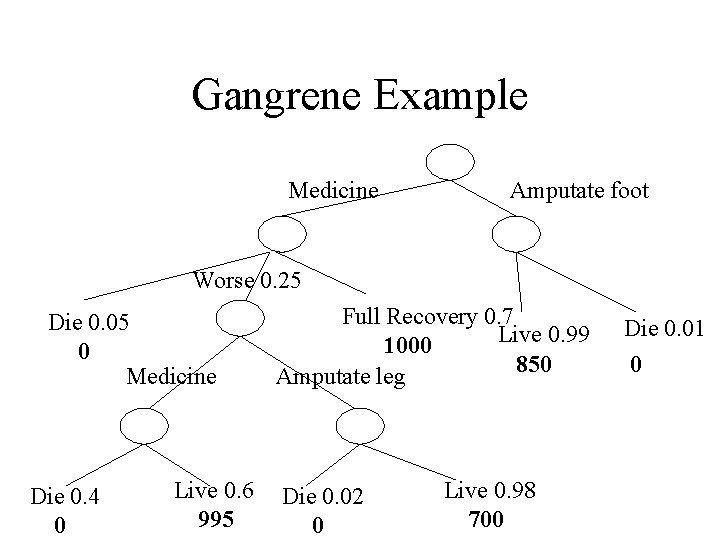
Gangrene Example Medicine Amputate foot Worse 0. 25 Die 0. 05 0 Medicine Die 0. 4 0 Live 0. 6 995 Full Recovery 0. 7 Live 0. 99 1000 850 Amputate leg Die 0. 02 0 Live 0. 98 700 Die 0. 01 0

Decision Tree Issues • Problem 1: Tree size – k activities : 2^k orders • Solution 1: Hill-climbing – Choose best apparent choice after one step • Use entropy reduction • Problem 2: Utility values – Difficult to estimate, Sensitivity, Duration • Change value depending on phrasing of question • Solution 2 c: Model effect of outcome over lifetime

Conclusion • Reasoning with uncertainty – Many real systems uncertain - e. g. medical diagnosis • Bayes’ Nets – Model (in)dependence relations in reasoning – Noisy-OR simplifies model/computation • Assumes causes independent • Decision Trees – Model rational decision making • Maximize outcome: Max choice, average outcomes

Holmes Example (Pearl) Holmes is worried that his house will be burgled. For the time period of interest, there is a 10^-4 a priori chance of this happening, and Holmes has installed a burglar alarm to try to forestall this event. The alarm is 95% reliable in sounding when a burglary happens, but also has a false positive rate of 1%. Holmes’ neighbor, Watson, is 90% sure to call Holmes at his office if the alarm sounds, but he is also a bit of a practical joker and, knowing Holmes’ concern, might (30%) call even if the alarm is silent. Holmes’ other neighbor Mrs. Gibbons is a well-known lush and often befuddled, but Holmes believes that she is four times more likely to call him if there is an alarm than not.

Holmes Example: Model There a four binary random variables: B: whether Holmes’ house has been burgled A: whether his alarm sounded W: whether Watson called G: whether Gibbons called

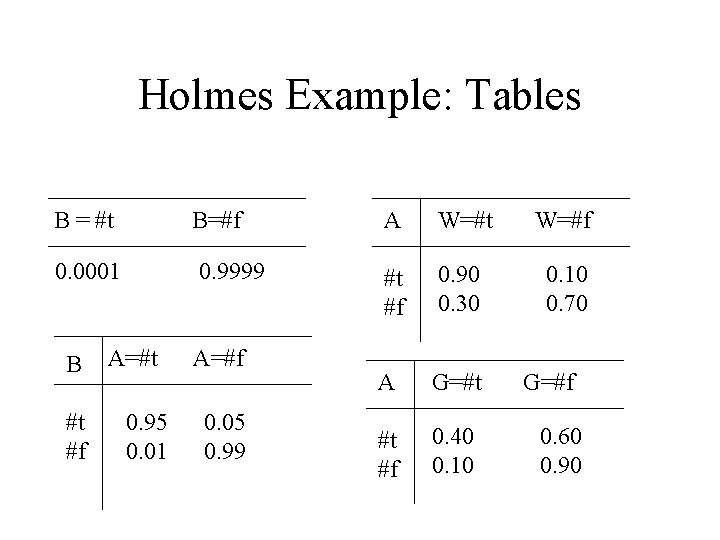
Holmes Example: Tables B = #t B=#f A W=#t W=#f 0. 0001 0. 9999 #t #f 0. 90 0. 30 0. 10 0. 70 A G=#t #t #f 0. 40 0. 10 B #t #f A=#t 0. 95 0. 01 A=#f 0. 05 0. 99 G=#f 0. 60 0. 90