Reasoning and Proof Logic Add to Vocabulary Definitions

Reasoning and Proof Logic

Add to Vocabulary / Definitions • • Statement Truth Value Negation Compound Statement Conjunction Disjunction Truth Tables

Statement A meaningful composition of words which can be considered either true or false is called a mathematical statement or simply a Statement. This is different from a conjecture. A single letter shall be used to denote a statement. Letters p and q are commonly used. For example, letter ‘p’ may be used to stand for the statement “ABC is an equilateral triangle. ” Thus, p = ABC is an equilateral triangle.

Truth Value The truth value of a statement is an evaluation of whether the statement is true or false. If p = 2 < 3 and q = 4 > 5 Thus, the truth value of p is true and q is false.

Negation • Negation refers to toggling a truth statement's truth value. The result is not always negative, or false, it is only the opposite of the original. Thus, the negation of "false" is "true. " This is denoted by a tilde (~) or the negation symbol. • If p is a statement then its negation ‘~p’ is statement ‘not p’, ‘~p’ has truth value F or T according as the truth value of ‘p’ is T or F.

Compound Statements • A compound statement is a sentence that consists of two or more statements separated by logical connectors. – Conjunctions (and) and disjunctions (or). – Implications (Implicators) (p implies q ), (If p holds then q), (If p then q), (q is necessary for p), (p is sufficient for q), (p is true exactly when q is true).

Conjunction • The sentence ‘p and q’ which may be denoted by ‘p Λq’ is the conjunction of p and q. Truth value of p Λ q is T only when both p and q are true. – An example might be the statement "3<6 and 4<6", which is true, since both statements "3<6" and "4<6" are true. The statement "3<6 and 4>6" is not true since "4>6" is false.

Disjunction • The sentence ‘p or q’ which may be denoted by ‘p V q’ is the disjunction of p and q. Truth value of p V q is T when either p or q are true. • The connector "or" is used to connect two statements and make a third statement whose truth value is based on the first two. The statement "P or Q" is true if either P or Q is true, or if both of them are true. Therefore, the statement, "The internet is complex or math is exciting. " is true, given that either or both statements are true, as is "7 > 9 or 2 < 3. " The only time the statement "P or Q" is false is when both P and Q are false, e. g. , "All people are Colombian or all Asians are tall. "

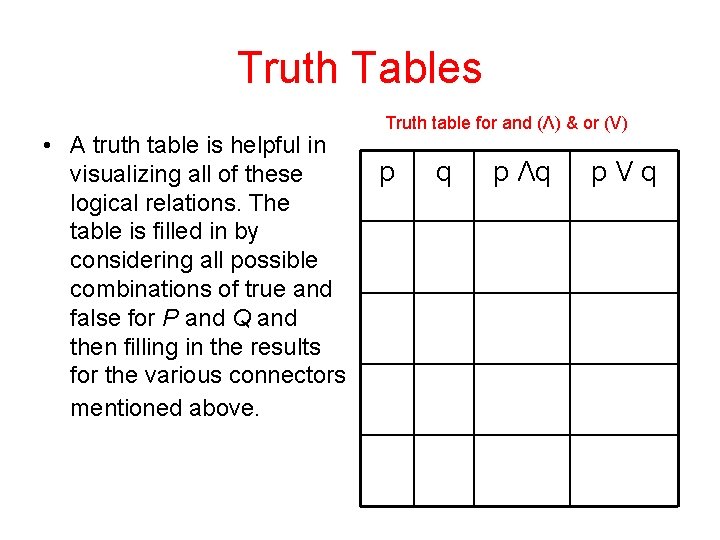
Truth Tables • A truth table is helpful in visualizing all of these logical relations. The table is filled in by considering all possible combinations of true and false for P and Q and then filling in the results for the various connectors mentioned above. Truth table for and (Λ) & or (V) p q p Λq p. Vq