Realistic Graph Generation and Evolution Using Kronecker Multiplication

Realistic Graph Generation and Evolution Using Kronecker Multiplication Jurij Leskovec, CMU Deepay Chakrabarti, CMU/Yahoo Jon Kleinberg, Cornell Christos Faloutsos, CMU 1

School of Computer Science Carnegie Mellon Introduction n Graphs are everywhere n What can we do with graphs? n What patterns or “laws” hold for most real-world graphs? n Can we build models of graph generation and evolution? “Needle exchange” networks of drug users 2

School of Computer Science Carnegie Mellon Outline n Introduction n Static graph patterns n Temporal graph patterns n Proposed graph generation model n Kronecker Graphs n Properties of Kronecker Graphs n Stochastic Kronecker Graphs n Experiments n Observations and Conclusion 3

School of Computer Science Carnegie Mellon Outline n Introduction n Static graph patterns n Temporal graph patterns n Proposed graph generation model n Kronecker Graphs n Properties of Kronecker Graphs n Stochastic Kronecker Graphs n Experiments n Observations and Conclusion 4

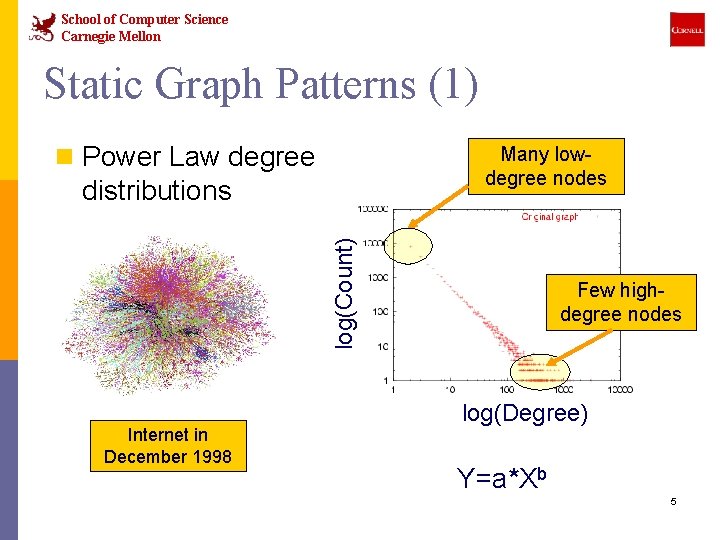
School of Computer Science Carnegie Mellon Static Graph Patterns (1) n Power Law degree Many lowdegree nodes log(Count) distributions Internet in December 1998 Few highdegree nodes log(Degree) Y=a*Xb 5

School of Computer Science Carnegie Mellon n Small-world [Watts, Strogatz]++ n 6 degrees of separation n Small diameter n Effective diameter: n Distance at which 90% of pairs of nodes are reachable # Reachable pairs Static Graph Patterns (2) Effective Diameter Hops Epinions who-trustswhom social network 6

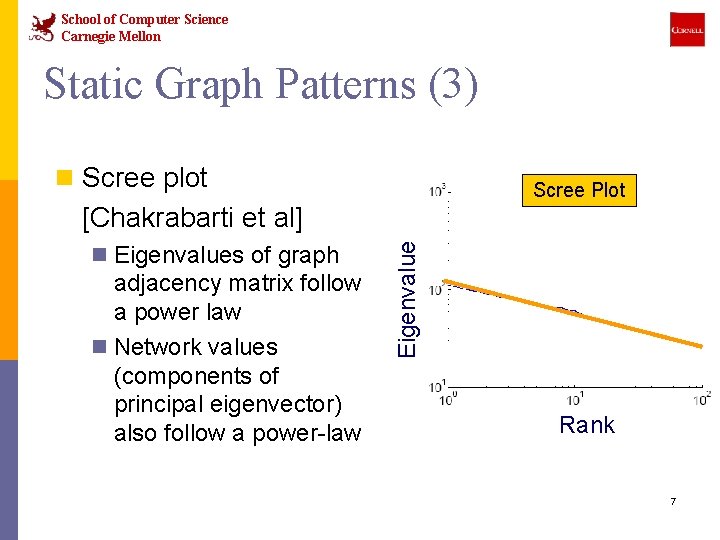
School of Computer Science Carnegie Mellon Static Graph Patterns (3) n Scree plot Scree Plot n Eigenvalues of graph adjacency matrix follow a power law n Network values (components of principal eigenvector) also follow a power-law Eigenvalue [Chakrabarti et al] Rank 7

School of Computer Science Carnegie Mellon Outline n Introduction n Static graph patterns n Temporal graph patterns n Proposed graph generation model n Kronecker Graphs n Properties of Kronecker Graphs n Stochastic Kronecker Graphs n Observations and Conclusion 8

School of Computer Science Carnegie Mellon Temporal Graph Patterns n Conventional Wisdom: n Constant average degree: the number of edges grows linearly with the number of nodes n Slowly growing diameter: as the network grows the distances between nodes grow n Recently found [Leskovec, Kleinberg and Faloutsos, 2005]: n Densification Power Law: networks are becoming denser over time n Shrinking Diameter: diameter is decreasing as the network grows 9

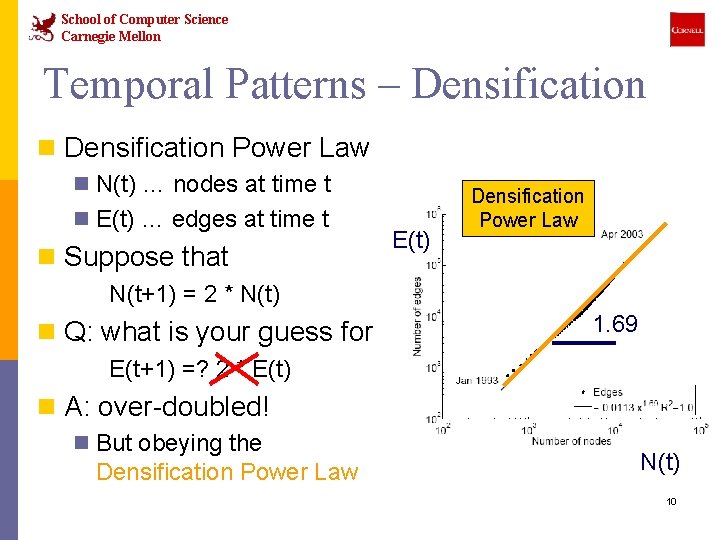
School of Computer Science Carnegie Mellon Temporal Patterns – Densification n Densification Power Law n N(t) … nodes at time t n E(t) … edges at time t n Suppose that E(t) Densification Power Law N(t+1) = 2 * N(t) n Q: what is your guess for 1. 69 E(t+1) =? 2 * E(t) n A: over-doubled! n But obeying the Densification Power Law N(t) 10

School of Computer Science Carnegie Mellon Temporal Patterns – Densification n Densification Power Law n networks are becoming denser over time n the number of edges grows faster than the number of nodes – average degree is increasing n Densification exponent a: 1 ≤ a ≤ 2: n a=1: linear growth – constant out-degree (assumed in the literature so far) n a=2: quadratic growth – clique 11

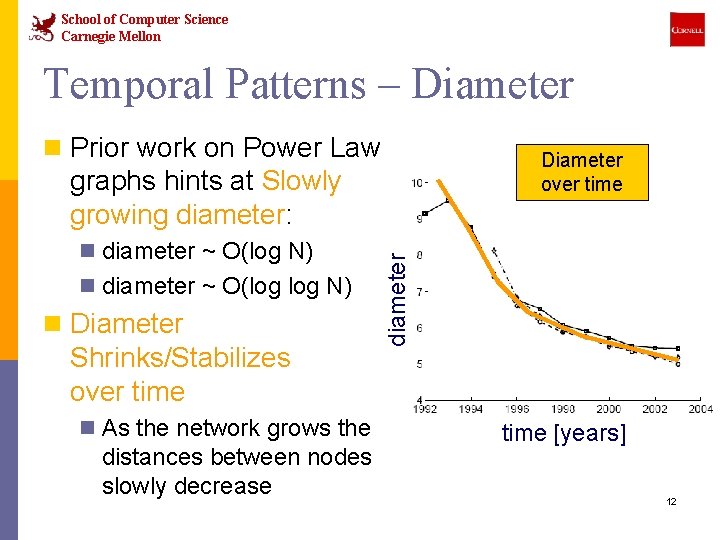
School of Computer Science Carnegie Mellon Temporal Patterns – Diameter n Prior work on Power Law Diameter over time n diameter ~ O(log N) n Diameter Shrinks/Stabilizes over time n As the network grows the distances between nodes slowly decrease diameter graphs hints at Slowly growing diameter: time [years] 12

School of Computer Science Carnegie Mellon Patterns hold in many graphs n All these patterns can be observed in many real life graphs: n World wide web [Barabasi] n On-line communities [Holme, Edling, Liljeros] n Who call whom telephone networks [Cortes] n Autonomous systems [Faloutsos, Faloutsos] n Internet backbone – routers [Faloutsos, Faloutsos] n Movie – actors [Barabasi] n Science citations [Leskovec, Kleinberg, Faloutsos] n Co-authorship [Leskovec, Kleinberg, Faloutsos] n Sexual relationships [Liljeros] n Click-streams [Chakrabarti] 13

School of Computer Science Carnegie Mellon Problem Definition n Given a growing graph with nodes N 1, N 2, … n Generate a realistic sequence of graphs that will obey all the patterns n Static Patterns n Power Law Degree Distribution n Small Diameter n Power Law eigenvalue and eigenvector distribution n Dynamic Patterns n Growth Power Law n Shrinking/Constant Diameters n And ideally we would like to prove them 14

School of Computer Science Carnegie Mellon Graph Generators n Lots of work n Random graph [Erdos and Renyi, 60 s] n Preferential Attachment [Albert and Barabasi, 1999] n Copying model [Kleinberg, Kumar, Raghavan, Rajagopalan and Tomkins, 1999] n Community Guided Attachment and Forest Fire Model [Leskovec, Kleinberg and Faloutsos, 2005] n Also work on Web graph and virus propagation [Ganesh et al, Satorras and Vespignani]++ n But all of these n Do not obey all the patterns n Or we are not able prove them 15

School of Computer Science Carnegie Mellon Why is all this important? n Simulations of new algorithms where real graphs are impossible to collect n Predictions – predicting future from the past n Graph sampling – many real world graphs are too large to deal with n What if scenarios 16

School of Computer Science Carnegie Mellon Outline n Introduction n Static graph patterns n Temporal graph patterns n Proposed graph generation model n Kronecker Graphs n Properties of Kronecker Graphs n Stochastic Kronecker Graphs n Observations and Conclusion 17

School of Computer Science Carnegie Mellon Problem Definition n Given a growing graph with count of nodes N 1, N 2, … n Generate a realistic sequence of graphs that will obey all the patterns n Idea: Self-similarity n Leads to power laws n Communities within communities n… 18

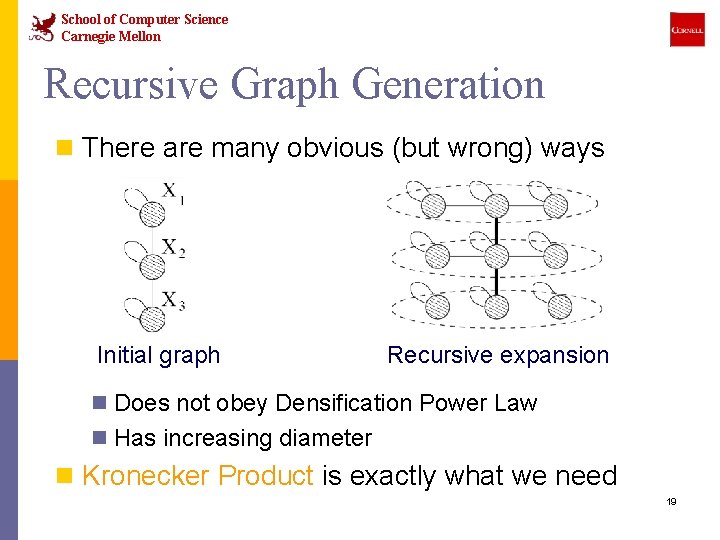
School of Computer Science Carnegie Mellon Recursive Graph Generation n There are many obvious (but wrong) ways Initial graph Recursive expansion n Does not obey Densification Power Law n Has increasing diameter n Kronecker Product is exactly what we need 19

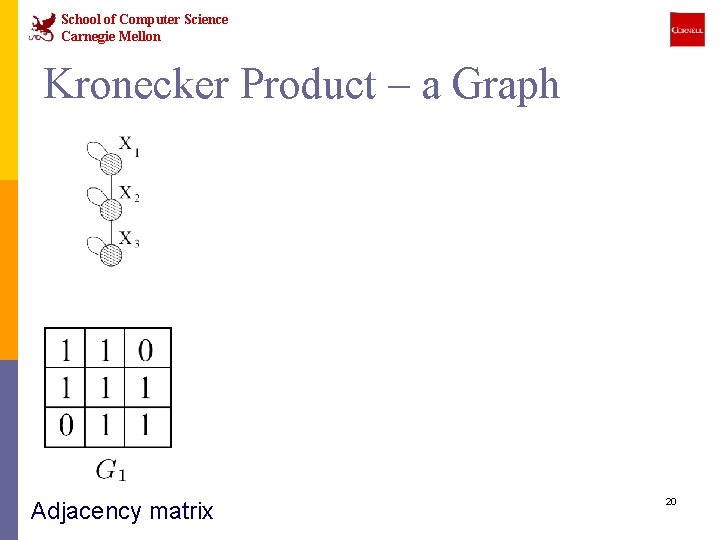
School of Computer Science Carnegie Mellon Kronecker Product – a Graph Intermediate stage Adjacency matrix 20

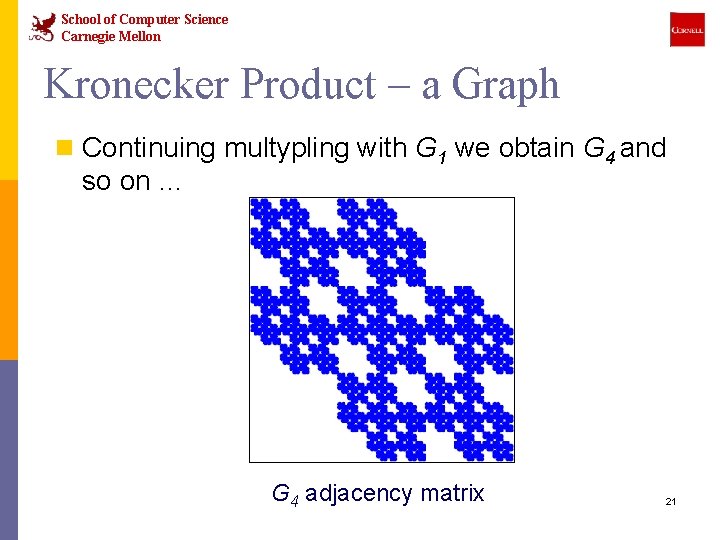
School of Computer Science Carnegie Mellon Kronecker Product – a Graph n Continuing multypling with G 1 we obtain G 4 and so on … G 4 adjacency matrix 21

School of Computer Science Carnegie Mellon Kronecker Graphs – Formally: n We create the self-similar graphs recursively: n Start with a initiator graph G 1 on N 1 nodes and E 1 edges n The recursion will then product larger graphs G 2, G 3, …Gk on N 1 k nodes n Since we want to obey Densification Power Law graph Gk has to have E 1 k edges 22

School of Computer Science Carnegie Mellon Kronecker Product – Definition n The Kronecker product of matrices A and B is given by Nx. M Kx. L N*K x M*L n We define a Kronecker product of two graphs as a Kronecker product of their adjacency matrices 23

School of Computer Science Carnegie Mellon Kronecker Graphs n We propose a growing sequence of graphs by iterating the Kronecker product n Each Kronecker multiplication exponentially increases the size of the graph 24

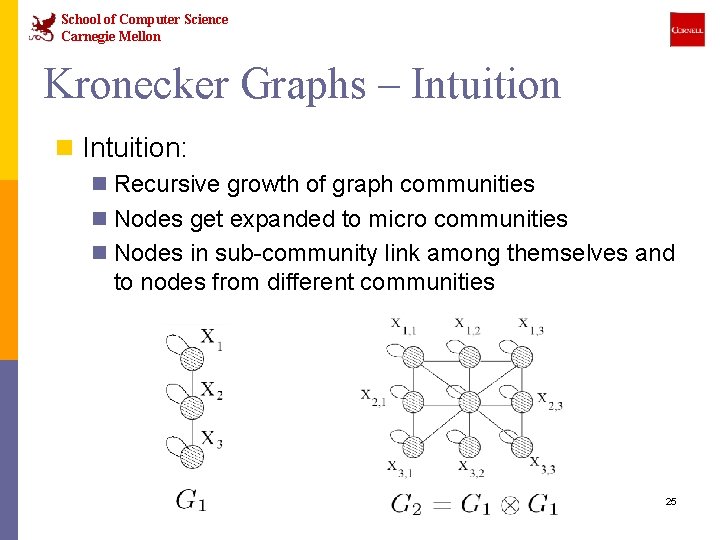
School of Computer Science Carnegie Mellon Kronecker Graphs – Intuition n Intuition: n Recursive growth of graph communities n Nodes get expanded to micro communities n Nodes in sub-community link among themselves and to nodes from different communities 25

School of Computer Science Carnegie Mellon Outline n Introduction n Static graph patterns n Temporal graph patterns n Proposed graph generation model n Kronecker Graphs n Properties of Kronecker Graphs n Stochastic Kronecker Graphs n Experiments n Conclusion 26

School of Computer Science Carnegie Mellon Problem Definition n Given a growing graph with nodes N 1, N 2, … n Generate a realistic sequence of graphs that will obey all the patterns n Static Patterns n Power Law Degree Distribution n Power Law eigenvalue and eigenvector distribution n Small Diameter n Dynamic Patterns n Growth Power Law n Shrinking/stabilizing Diameters 27

School of Computer Science Carnegie Mellon Problem Definition n Given a growing graph with nodes N 1, N 2, … n Generate a realistic sequence of graphs that will obey all the patterns n Static Patterns n Power Law Degree Distribution n Power Law eigenvalue and eigenvector distribution n Small Diameter n Dynamic Patterns n Growth Power Law n Shrinking/stabilizing Diameters 28

School of Computer Science Carnegie Mellon Properties of Kronecker Graphs n Theorem: Kronecker Graphs have Multinomial in- and out-degree distribution (which can be made to behave like a Power Law) n Proof: n Let G 1 have degrees d 1, d 2, …, d. N n Kronecker multiplication with a node of degree d gives degrees d∙d 1, d∙d 2, …, d∙d. N n After Kronecker powering Gk has multinomial degree distribution 29

School of Computer Science Carnegie Mellon Eigen-value/-vector Distribution n Theorem: The Kronecker Graph has multinomial distribution of its eigenvalues n Theorem: The components of each eigenvector in Kronecker Graph follow a multinomial distribution n Proof: Trivial by properties of Kronecker multiplication 30

School of Computer Science Carnegie Mellon Problem Definition n Given a growing graph with nodes N 1, N 2, … n Generate a realistic sequence of graphs that will obey all the patterns n Static Patterns Power Law Degree Distribution Power Law eigenvalue and eigenvector distribution Small Diameter n Dynamic Patterns n Growth Power Law n Shrinking/Stabilizing Diameters 31

School of Computer Science Carnegie Mellon Problem Definition n Given a growing graph with nodes N 1, N 2, … n Generate a realistic sequence of graphs that will obey all the patterns n Static Patterns Power Law Degree Distribution Power Law eigenvalue and eigenvector distribution Small Diameter n Dynamic Patterns n Growth Power Law n Shrinking/Stabilizing Diameters 32

School of Computer Science Carnegie Mellon Temporal Patterns: Densification n Theorem: Kronecker graphs follow a Densification Power Law with densification exponent n Proof: n If G 1 has N 1 nodes and E 1 edges then Gk has Nk = N 1 k nodes and Ek = E 1 k edges n And then Ek = Nka n Which is a Densification Power Law 33

School of Computer Science Carnegie Mellon Constant Diameter n Theorem: If G 1 has diameter d then graph Gk also has diameter d n Theorem: If G 1 has diameter d then q-effective diameter if Gk converges to d n q-effective diameter is distance at which q% of the pairs of nodes are reachable 34

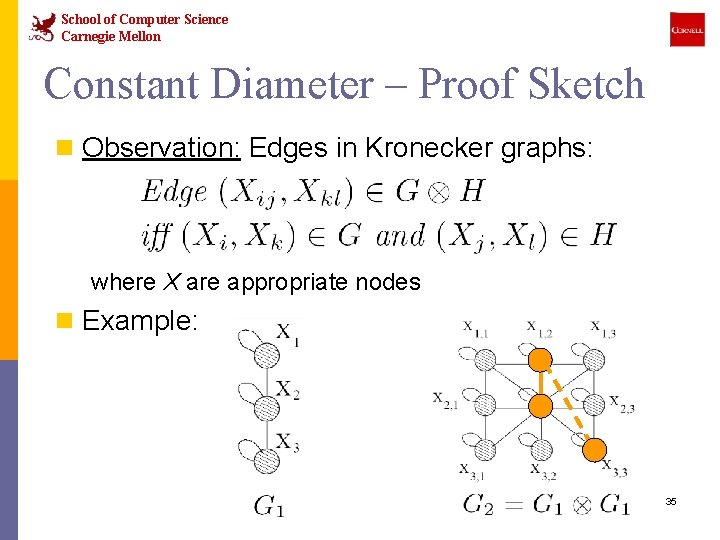
School of Computer Science Carnegie Mellon Constant Diameter – Proof Sketch n Observation: Edges in Kronecker graphs: where X are appropriate nodes n Example: 35

School of Computer Science Carnegie Mellon Problem Definition n Given a growing graph with nodes N 1, N 2, … n Generate a realistic sequence of graphs that will obey all the patterns n Static Patterns Power Law Degree Distribution Power Law eigenvalue and eigenvector distribution Small Diameter n Dynamic Patterns Growth Power Law Shrinking/Stabilizing Diameters n First and the only generator for which we can prove all the properties 36

School of Computer Science Carnegie Mellon Outline n Introduction n Static graph patterns n Temporal graph patterns n Proposed graph generation model n Kronecker Graphs n Properties of Kronecker Graphs n Stochastic Kronecker Graphs n Experiments n Observations and Conclusion 37

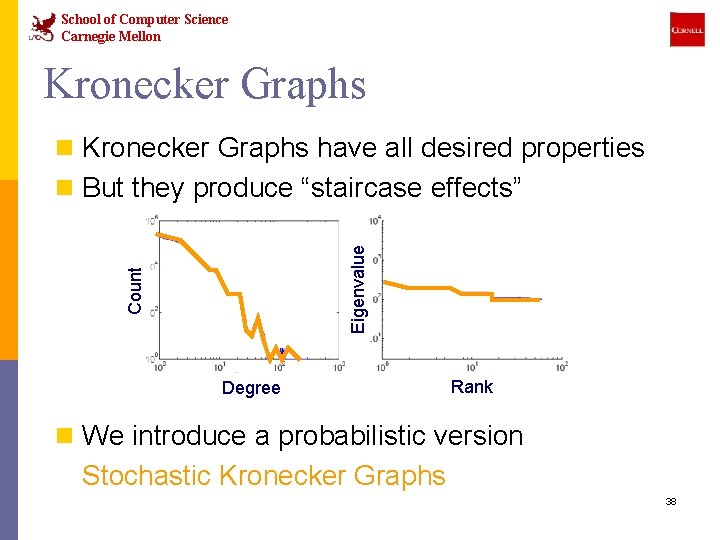
School of Computer Science Carnegie Mellon Kronecker Graphs have all desired properties Count Eigenvalue n But they produce “staircase effects” Degree Rank n We introduce a probabilistic version Stochastic Kronecker Graphs 38

School of Computer Science Carnegie Mellon How to randomize a graph? n We want a randomized version of Kronecker Graphs n Obvious solution n Randomly add/remove some edges n Wrong! – is not biased n adding random edges destroys degree distribution, diameter, … n Want add/delete edges in a biased way n How to randomize properly and maintain all the properties? 39

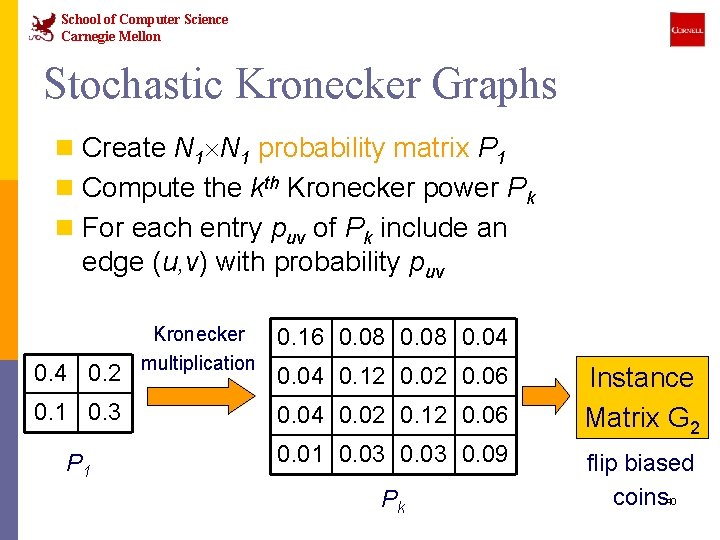
School of Computer Science Carnegie Mellon Stochastic Kronecker Graphs n Create N 1 probability matrix P 1 n Compute the kth Kronecker power Pk n For each entry puv of Pk include an edge (u, v) with probability puv 0. 4 0. 2 Kronecker multiplication 0. 16 0. 08 0. 04 0. 12 0. 06 0. 1 0. 3 0. 04 0. 02 0. 12 0. 06 P 1 0. 03 0. 09 Pk Instance Matrix G 2 flip biased coins 40

School of Computer Science Carnegie Mellon Outline n Introduction n Static graph patterns n Temporal graph patterns n Proposed graph generation model n Kronecker Graphs n Properties of Kronecker Graphs n Stochastic Kronecker Graphs n Experiments n Conclusion 41

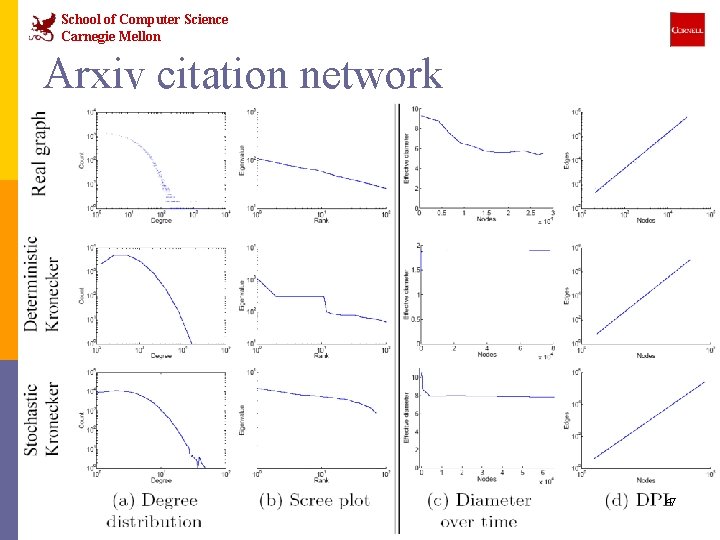
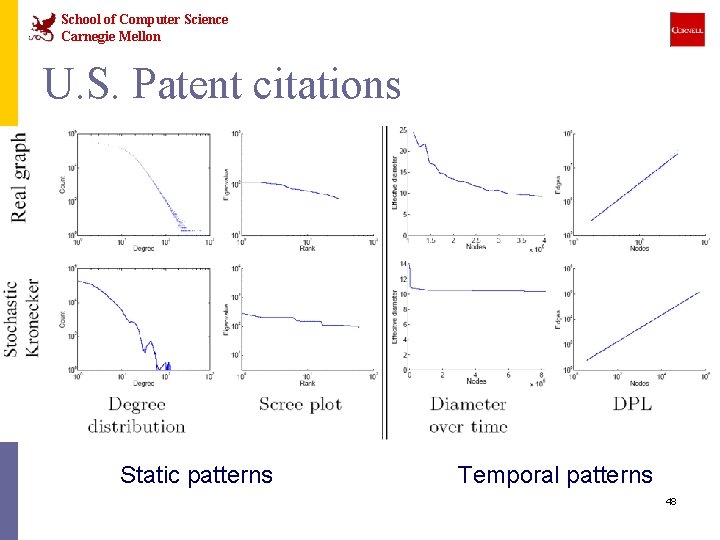
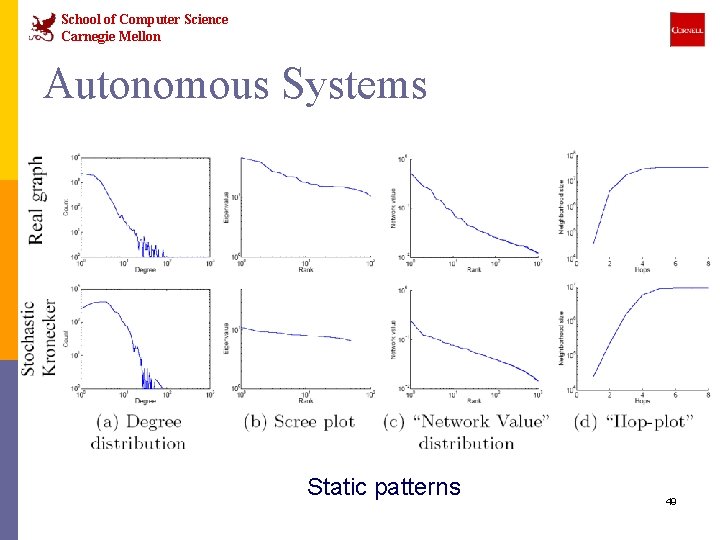
School of Computer Science Carnegie Mellon Experiments n How well can we match real graphs? n Arxiv: physics citations: n 30, 000 papers, 350, 000 citations n 10 years of data n U. S. Patent citation network n 4 million patents, 16 million citations n 37 years of data n Autonomous systems – graph of internet n Single snapshot from January 2002 n 6, 400 nodes, 26, 000 edges n We show both static and temporal patterns 42

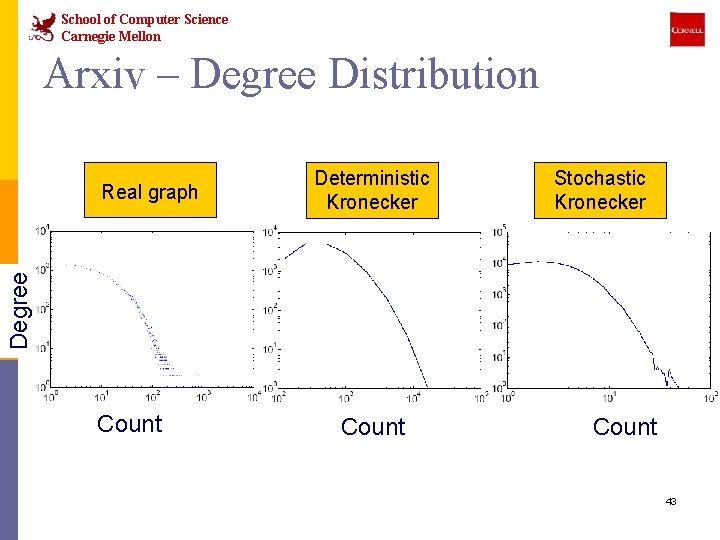
School of Computer Science Carnegie Mellon Arxiv – Degree Distribution Deterministic Kronecker Stochastic Kronecker Degree Real graph Count 43

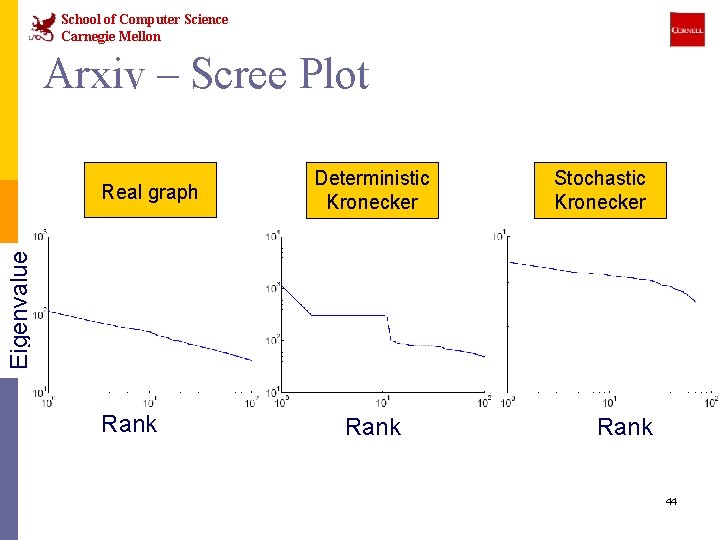
School of Computer Science Carnegie Mellon Arxiv – Scree Plot Deterministic Kronecker Stochastic Kronecker Eigenvalue Real graph Rank 44

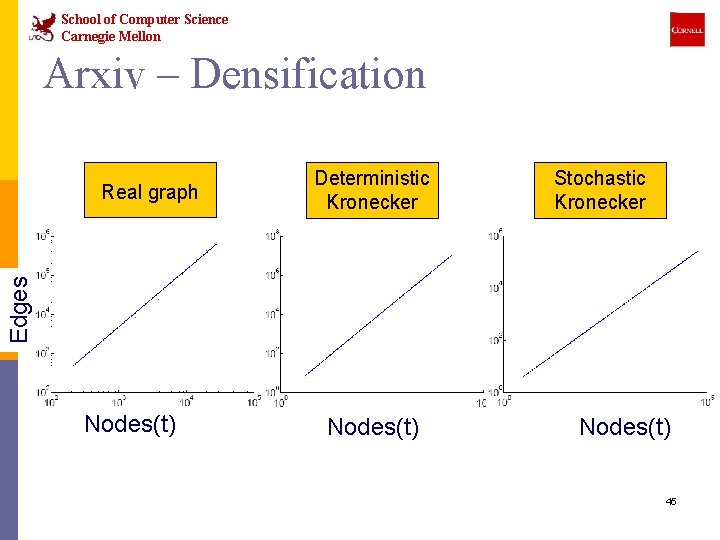
School of Computer Science Carnegie Mellon Arxiv – Densification Deterministic Kronecker Stochastic Kronecker Edges Real graph Nodes(t) 45

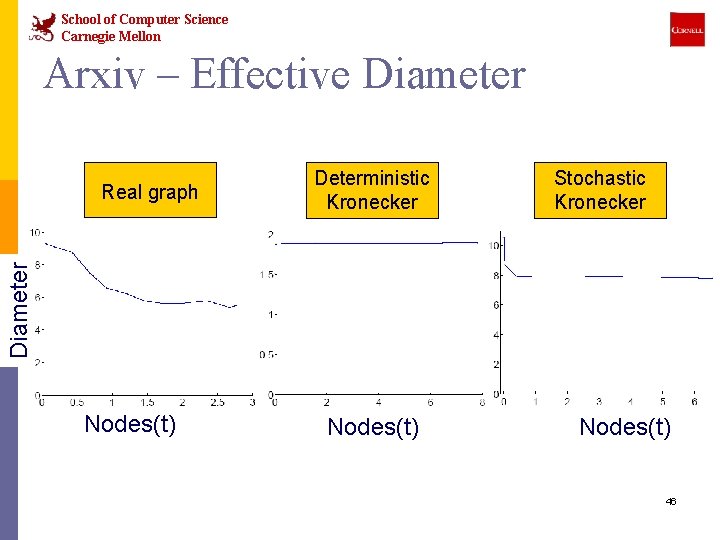
School of Computer Science Carnegie Mellon Arxiv – Effective Diameter Deterministic Kronecker Stochastic Kronecker Diameter Real graph Nodes(t) 46

School of Computer Science Carnegie Mellon Arxiv citation network 47

School of Computer Science Carnegie Mellon U. S. Patent citations Static patterns Temporal patterns 48

School of Computer Science Carnegie Mellon Autonomous Systems Static patterns 49

School of Computer Science Carnegie Mellon How to choose initiator G 1? n Open problem n Kronecker division/root n Work in progress n We used heuristics n We restricted the space of all parameters n Details are in the paper 50

School of Computer Science Carnegie Mellon Outline n Introduction n Static graph patterns n Temporal graph patterns n Proposed graph generation model n Kronecker Graphs n Properties of Kronecker Graphs n Stochastic Kronecker Graphs n Experiments n Observations and Conclusion 51

School of Computer Science Carnegie Mellon Observations n Generality n Stochastic Kronecker Graphs include Erdos-Renyi model and RMAT graph generator as a special case n Phase transitions n Similarly to Erdos-Renyi model Kronecker graphs exhibit phase transitions in the size of giant component and the diameter n We think n additional properties will be easy to prove (clustering coefficient, number of triangles, …) 52

School of Computer Science Carnegie Mellon Conclusion (1) n We propose a family of Kronecker Graph generators n We use the Kronecker Product n We introduce a randomized version Stochastic Kronecker Graphs 53

School of Computer Science Carnegie Mellon Conclusion (2) n The resulting graphs have n All the static properties Heavy tailed degree distributions Small diameter Multinomial eigenvalues and eigenvectors n All the temporal properties Densification Power Law Shrinking/Stabilizing Diameters n We can formally prove these results 54

School of Computer Science Carnegie Mellon Thank you! Questions? jure@cs. cmu. edu 55

School of Computer Science Carnegie Mellon Stochastic Kronecker Graphs n We define Stochastic Kronecker Graphs n Start with N 1 probability matrix P 1 n where pij denotes probability that edge (i, j) is present n Compute the kth Kronecker power Pk n For each entry puv of Pk we include an edge (u, v) with probability puv 56