Real time pattern matching Porat Benny Porat Ely

Real time pattern matching Porat Benny Porat Ely Bar-Ilan University

Pattern Matching Given a Text T and Pattern P, the problem is to find all the substring of T that equal to P. T= P=
Online pattern matching =P We get the text character by character

Outline Motivation Presentation of 3 online models Space lower bound A black box algorithm Exact and approximate pattern matching in the streaming model

Motivation… Monitoring internet traffic
Motivation… Stock market

Motivation. . Espionage

Motivation… Viruses and malware
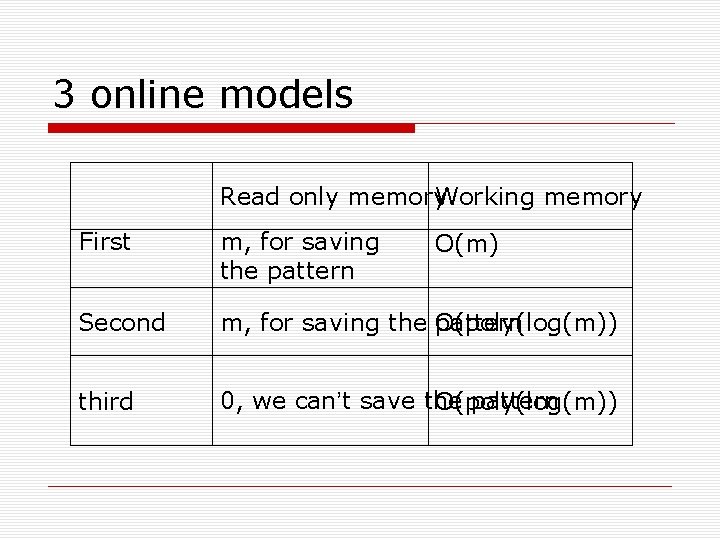
3 online models Read only memory Working memory First m, for saving the pattern Second m, for saving the O(poly(log(m)) pattern third 0, we can’t save the pattern O(poly(log(m)) O(m)
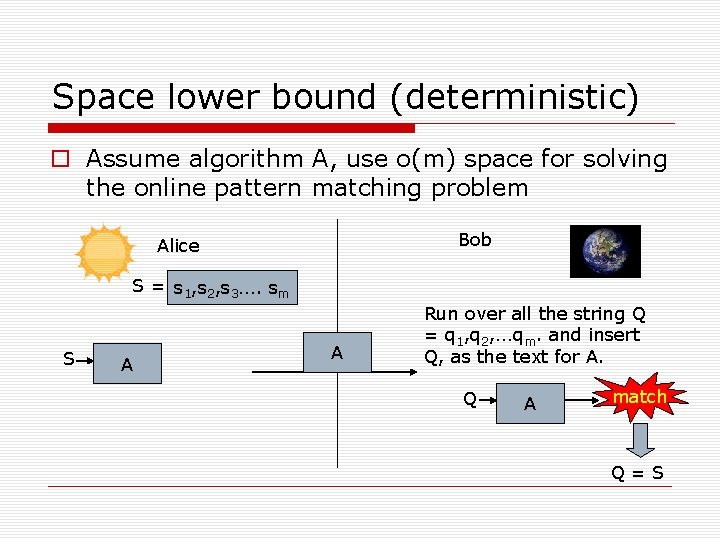
Space lower bound (deterministic) Assume algorithm A, use o(m) space for solving the online pattern matching problem Bob Alice S = s 1, s 2, s 3…. sm S A A Run over all the string Q = q 1, q 2, …qm. and insert Q, as the text for A. Q A match Q=S

A black box for online approximate pattern matching Raphaël Clifford Benny Porat Ely Porat CPM 2008

Black box for the First model Read only memory Working memory First m, for saving the. O(m) pattern

Problem definition There a lot of offline pattern matching algorithms. pseudo real time – take the best time of the offline algorithm, divide it by n And this is bound the time per character. Not Amortized!! We want to find a black box algorithm, that takes most offline pattern matching algorithms and converts them to be pseudo real time.

Result In example, we can applied our algorithm to the flowing problem Hamming norm K-mismatch Matching under L 2 Matching under L 1 Online Convolution. .

Exact And Approximate Pattern Matching In The Streaming Model Porat Benny Porat Ely FOCS 2009

solution for the third model Read only memory Working memory third 0, we can’t save O(poly(log(m)) the pattern Pattern Matching up to k mistake
It’s not minor! Cache Work much faster then the Ram Researchers that there is a Now it’s canthought fit! lower bound and it can't be done. Anti virus on routers

Randomized algorithm (RK) All the calculation in Fq pm-1, …p 2, p 1, p 0 t 1, t 2, t 3, … ti , ti+1, ti+2 , …tm, tm+1, … tn How can I calculate from without remembering ti ? ? ?
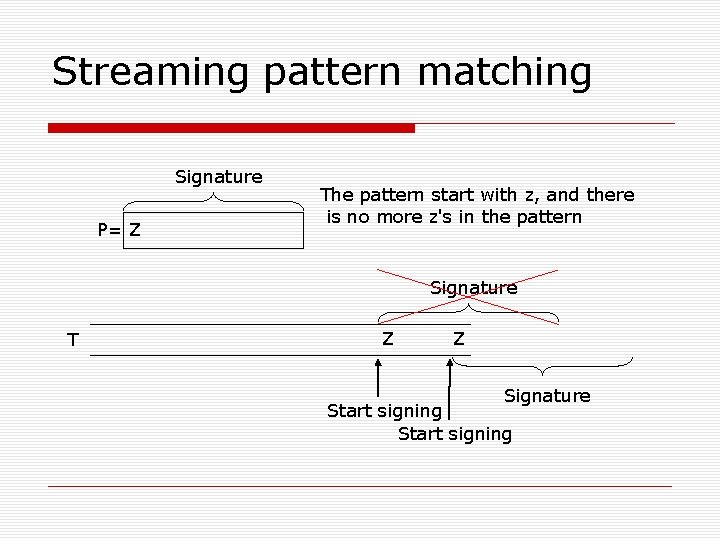
Streaming pattern matching Signature P= Z The pattern start with z, and there is no more z's in the pattern Signature T Z Z Signature Start signing

No Z Signature P= U =<m/2 Seek in recursion T There is a prefix U s. t U appear only once in the pattern m Signature U U Signature Start signing
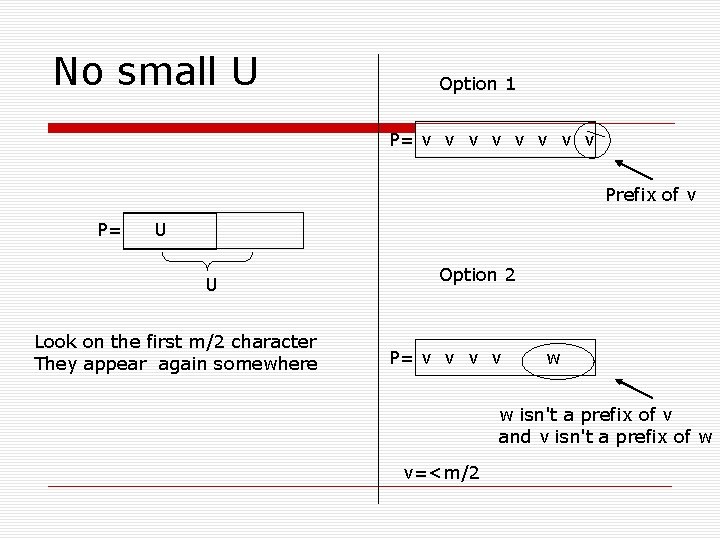
No small U Option 1 P= v v v v Prefix of v P= U U Look on the first m/2 character They appear again somewhere Option 2 P= v v w w isn't a prefix of v and v isn't a prefix of w v=<m/2

Solving this case Option 2 P= v v v=<m/2 w Sign on w Search in recursion for v, and count how many time you found it T Signature v v v Start signing

Solving this case - continue Option 2 P= v v v=<m/2 w Sign on w Search in recursion for v, and count how many time you found it T v v <m/2 Signature vv v v >m/2 Start signing Using O(log m) signatures and counters in the worst case Time = O(log m) in the worst case

Pattern Matching up to k mistake 1 – mismatch Pattern Matching up to k mistake

Chinese Remainder Theorem Lets n and m be two coprimes.
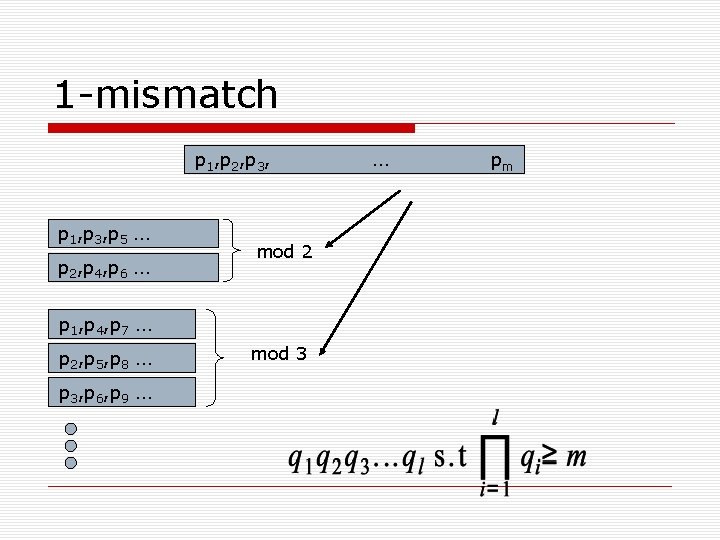
1 -mismatch p 1, p 2, p 3, p 1, p 3, p 5 … p 2, p 4, p 6 … mod 2 p 1, p 4, p 7 … p 2, p 5, p 8 … p 3, p 6, p 9 … mod 3 … pm

1 -mismatch p 1, p 3, p 5 … p 2, p 4, p 6 … mod 2 Overall sum of all primes p 1, p 3, p 5 … t 1, t 3, t 5 … p 1, p 4, p 7 … p 2, p 5, p 8 … p 3, p 6, p 9 … mod 3 p 2, p 4, p 6 … t 2, t 4, t 6 …

1 -mismatch p 1, p 3, p 5 … p 2, p 4, p 6 … mod 2 p 1, p 3, p 5 … t 1, t 3, t 5 … p 2, p 4, p 6 … t 2, t 4, t 6 …
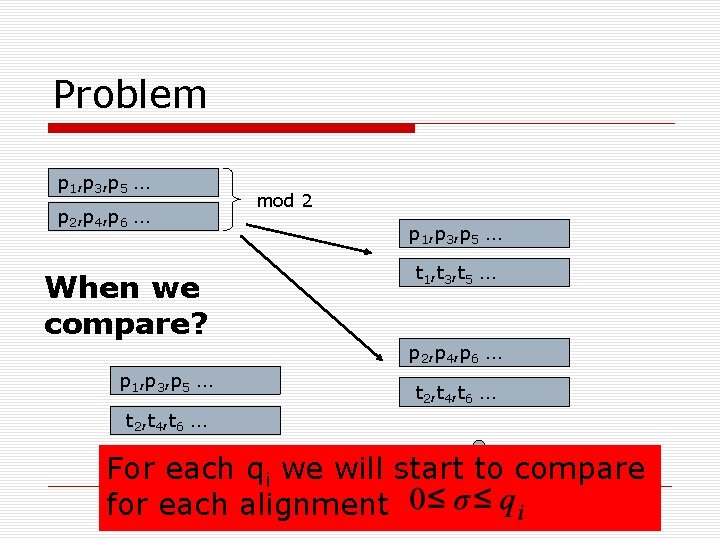
Problem p 1, p 3, p 5 … p 2, p 4, p 6 … When we compare? mod 2 p 1, p 3, p 5 … t 1, t 3, t 5 … p 2, p 4, p 6 … p 1, p 3, p 5 … t 2, t 4, t 6 … For each qi we will start to compare for each alignment

Space complexity For each qi we run qi time our algorithm for each alignment. For each alignment we run again qi time for each shift. Overall:

Time complexity Each character go to just one alignment for each shift. Overall:

1 -mismatch Lemma 1 There is exactly one mismatch There is exactly one subpattern in each group that not match. C. R. T

Pattern Matching up to k mistake Group testing/ Random selector…

A black box for online approximate pattern matching Raphaël Clifford Benny Porat Ely Porat CPM 2008
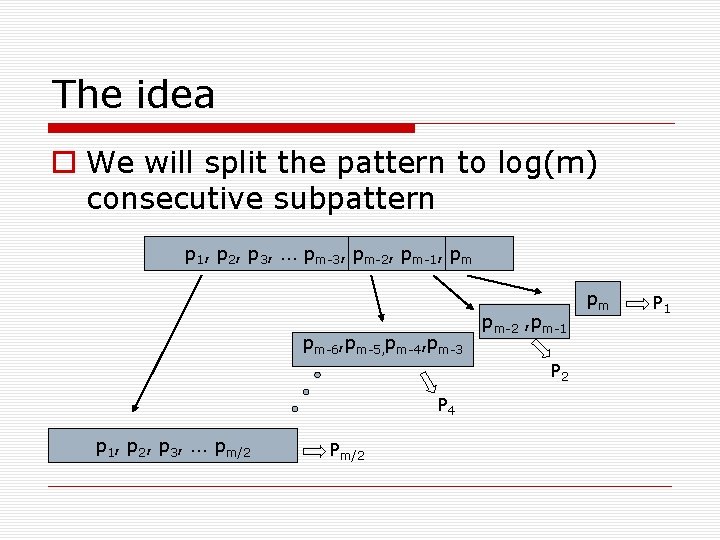
The idea We will split the pattern to log(m) consecutive subpattern p 1, p 2, p 3, … pm-3, pm-2, pm-1, pm pm-6, pm-5, pm-4, pm-3 pm-2 , pm-1 P 2 P 4 p 1, p 2, p 3, … pm/2 Pm/2 pm P 1

Bring it online Let look on subpattern with length m’=>Pm’ When we got to the i’th character of the text, to where is Pm’ align? m … … Pm’ m’ … ti pm-1 pm-2 pm m’-1 Conclusion 1 We need to know DIFF(Pm’, T(i-m’, i)) just at position i+m’ of the text.
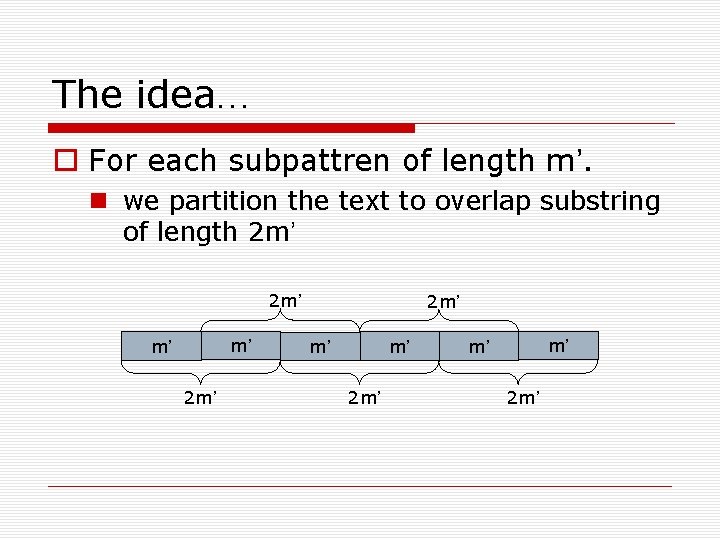
The idea… For each subpattren of length m’. we partition the text to overlap substring of length 2 m’ 2 m’ m’ m’ 2 m’

The idea… For each subpattren of length m’ we run the offline algorithm on each partition of the text separately. 2 m’ m’ We will got all the differences for this section ti If i=2 lm’ or 2 lm’+m’ for some l run the offline algorithm on last 2 m’ character. This ensure us, that we got the difference on time. the

Running Time T(n, m)=n. T(m) – the running time of the offline algorithm For each subpattern of length m’ We got overlap partition. total time for each subpattrn: Total time:

The problem We saw, that overall the time is good But, m’ = m/2 ti 2 tm’+m’ 2 m’ = m Pm/2 m’ = m/2 2 m’ = m 2(t+1)m’ We must wait until the run of the offline algorithm on Pm/2 and the last m character to finish, before we can return the answer for. => (m/2)T(m) time!
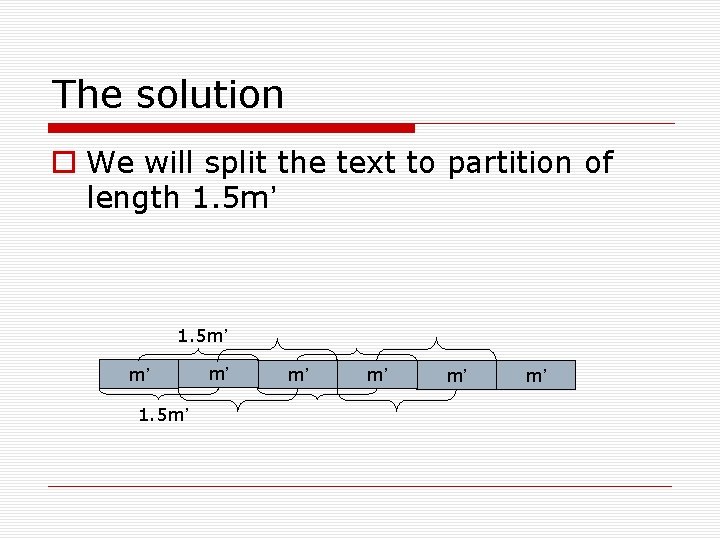
The solution We will split the text to partition of length 1. 5 m’ m’ m’

The solution… The latest we will get DIFF(Pm’, Ti-m’, i) will be at index i+m’/2 Conclusion 1. We need to know DIFF(Pm’, Ti-m’, i) just at position i+m’ of the text. And by Conclusion 1, we can wait m’/2 character, before we will need this difference.
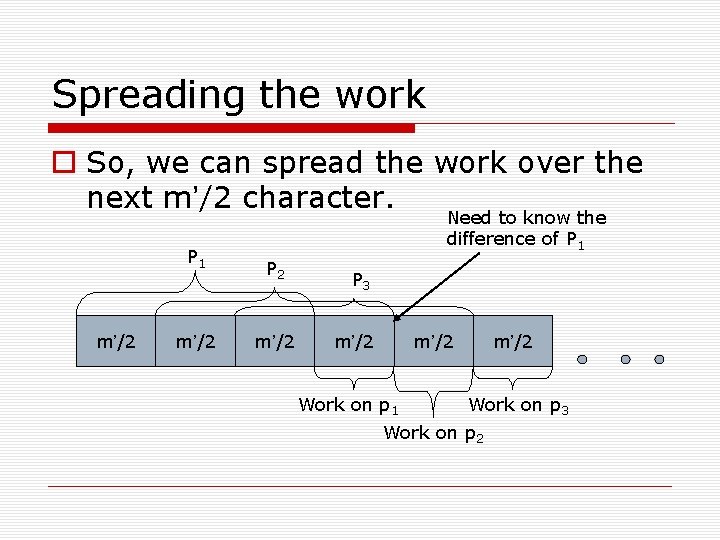
Spreading the work So, we can spread the work over the next m’/2 character. Need to know the P 1 m’/2 difference of P 1 P 2 m’/2 P 3 m’/2 Work on p 1 m’/2 Work on p 3 Work on p 2

Spreading the work… Overall, we can spread the work for a specific subpattern equivalently between all the character of the text. All we left to do, is to check that the running time, not change.

Running Time T(n, m)=n. T(m) – the running time of the offline algorithm For each subpattern of length m’ Now, We got overlap partition. total time for each subpattrn: Total time for all the text: Not change!

Running Time… By spreading the work we got total running time for each character

conclusion We give a space lower bound for deterministic online pattern matching We give a black box algorithm that can adapt any offline algorithm to online algorithm, using only O(m) space and take time per character.
- Slides: 47