Real Numbers and Their Properties CCSS N RN

Real Numbers and Their Properties CCSS: N. RN. 3

v. Domain: The Real Number System v. Clusters: Use properties of rational and irrational numbers v. Standards: EXPLAIN why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a nonzero rational number and an irrational number is irrational. N. RN. 3

Write sets using set notation A set is a collection of objects called the elements or members of the set. Set braces { } are usually used to enclose the elements. In Algebra, the elements of a set are usually numbers. Example 1: 3 is an element of the set {1, 2, 3} Note: This is referred to as a Finite Set since we can count the elements of the set. Example 2: N= {1, 2, 3, 4, …} is referred to as a Natural Numbers or Counting Numbers Set. Example Set. 3: W= {0, 1, 2, 3, 4, …} is referred to as a Whole Number

Write sets using set notation A set is a collection of objects called the elements or members of the set. Set braces { } are usually used to enclose the elements. Example 4: A set containing no numbers is shown as { } Note: This is referred to as the Null Set or Empty Set. Caution: Do not write the {0} set as the null set. This set contains one element, the number 0. Example 5: To show that 3 “is a element of” the set {1, 2, 3}, use the notation: 3 {1, 2, 3}. Note: This is also true: 3 N Example 6: 0 N where is read as “is not an element of set”

Write sets using set notation Two sets are equal if they contain exactly the same elements. (Order doesn’t matter) Example 1: {1, 12} = {12, 1} Example 2: {0, 1, 3} {0, 2, 3}

Write sets using set notation In Algebra, letters called variables are often used to represent numbers or to define sets of numbers. (x or y). The notation {x|x has property P}is an example of “Set Builder Notation” and is read as: {x x has property P} the set of Example all elements x such that x has a property P 1: {x|x is a whole number less than 6} Solution: {0, 1, 2, 3, 4, 5}

Write sets using set notation In Algebra, letters called variables are often used to represent numbers or to define sets of numbers. (x or y). The notation {x|x has property P}is an example of “Set Builder Notation” and is read as: {x x has property P} the set of Example all elements x such that x has a property P 2: {x|x is a natural number greater than 12} Solution: {13, 14, 15, …}

Using a number line -2 v One -1 0 1 2 3 4 5 way to visualize a set a numbers is to use a “Number Line”. Example 1: The set of numbers shown above includes positive numbers, negative numbers and 0. This set is part of the set of “Integers” and is written: I = {…, -2, -1, 0, 1, 2, …}

Using a number line Graph of -1 o -2 -1 o 0 o 1 2 3 4 5 coordinate v. Each number on a number line is called the coordinate of the point that it labels, while the point is the graph of the number. Example 1: The fractions shown above are examples of rational numbers. A rational number is one than can be expressed as the quotient of two integers, with the denominator not 0.

Using a number line Graph of -1 o -2 -1 o 0 o 1 o 2 oo o 3 o 4 5 coordinate v. Decimal numbers that neither terminate nor repeat are called “irrational numbers”. Example 1: Many square roots are irrational numbers, however some square roots are rational. Irrational: Rational:

The common sets of numbers v. The following sets of numbers will be used for this course: N - Natural numbers or Counting Numbers: {1, 2, 3, …} W – Whole numbers: {0, 1, 2, 3, …} I – Integer numbers: {…, -2, -1, 0, 1, 2, …} R - Rational numbers: IR – Irrational numbers: {x| x is a real number that is not rational} RN- Real numbers: {x| x is represented by a point on a number line}

The Real Number System Real Numbers Rational Numbers Irrational Numbers 1/2 -2 3 3 0 15% -0. 7 1. 456 10/21/2021 2/3 3 4 2 - 5 2

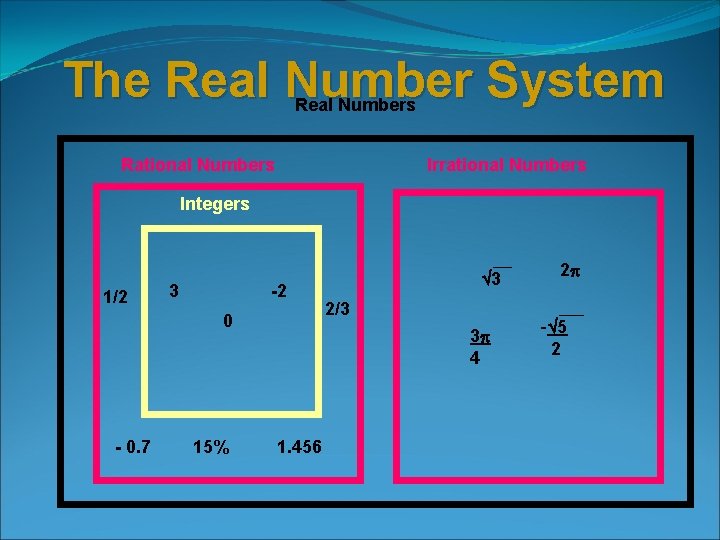
The Real Number System Real Numbers Rational Numbers Irrational Numbers Integers 1/2 3 -2 0 - 0. 7 15% 3 2/3 3 4 1. 456 2 - 5 2

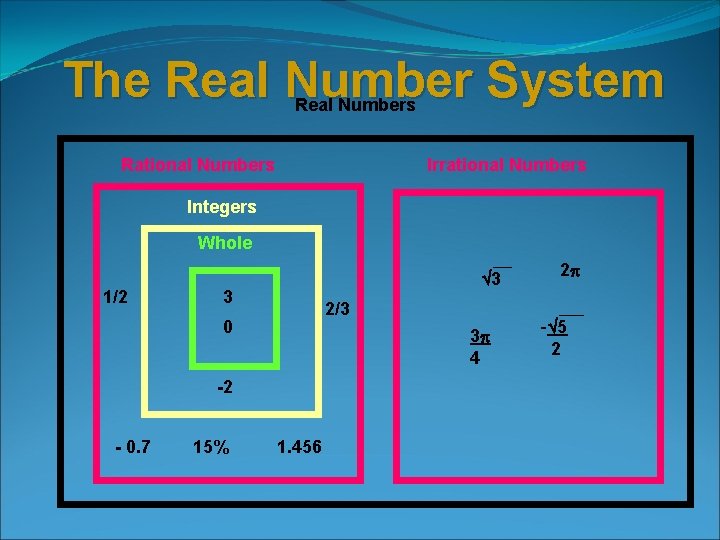
The Real Number System Real Numbers Rational Numbers Irrational Numbers Integers Whole 1/2 3 3 2/3 0 3 4 -2 - 0. 7 15% 1. 456 2 - 5 2

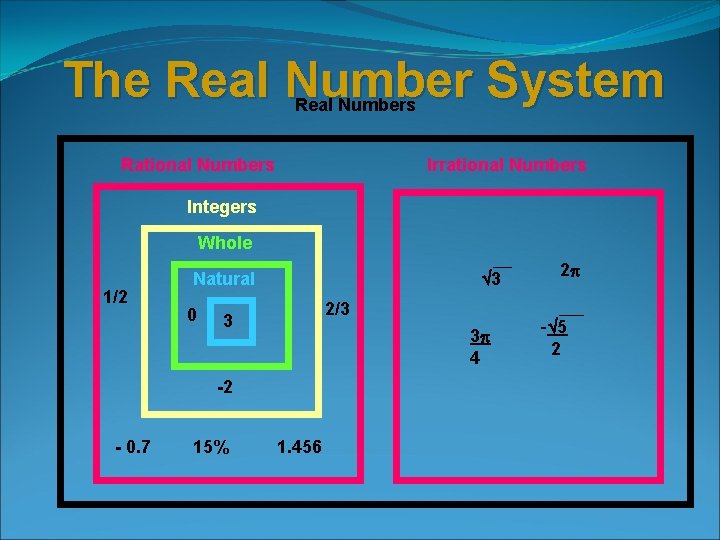
The Real Number System Real Numbers Rational Numbers Irrational Numbers Integers Whole 1/2 3 Natural 0 2/3 3 3 4 -2 - 0. 7 15% 1. 456 2 - 5 2

The common sets of numbers v. Question: Select all the words from the following list that apply to the number: Whole Number, Rational Number, Irrational Number, Real Number, Undefined Solution: Whole Number, Rational Number, Real Number

Finding Additive inverses v. For any real number x, the number –x is the additive inverse of x. Example 1:

Using the Absolute Value v Examples: Find : To find the absolute value of a signed number: Caution: The absolute value of a number is always positive

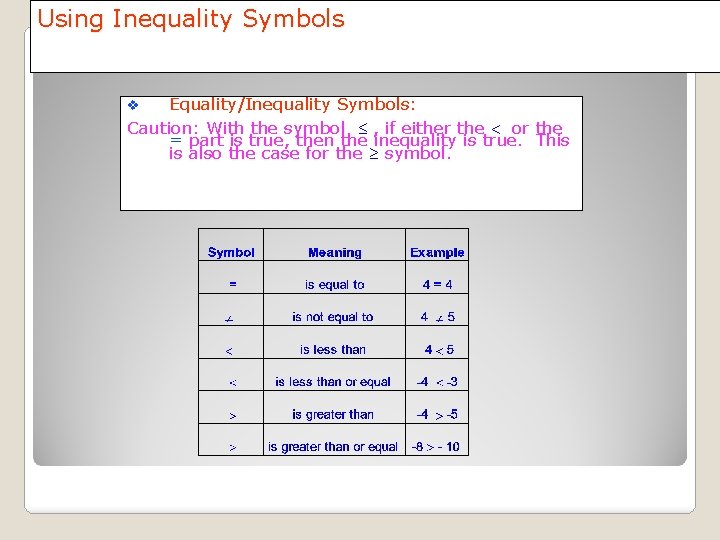
Using Inequality Symbols Equality/Inequality Symbols: Caution: With the symbol , if either the or the = part is true, then the inequality is true. This is also the case for the symbol. v

Graphing Sets of Real Numbers A parenthesis ( or ) is used to indicate a number is not an element of a set. A bracket [ or ] is used to indicate a number is a member of a set. v Example 1: Write in interval notation and graph: {x|x 3} Solution: Interval Notation (- , 3) ) -2 -1 0 1 2 3 4 5 Example 2: Write in interval notation and graph: {x|x 0} Solution: Interval Notation [0, ) [ -2 -1 0 1 2 3 4 5

Graphing Sets of Real Numbers A parenthesis ( or ) is used to indicate a number is not an element of a set. A bracket [ or ] is used to indicate a number is a member of a set. v Example 3: Write in interval notation and graph: {x| -2 x 3} Solution: Interval Notation [-2, 3) [ -2 ) -1 0 1 2 3 4 5