Reading The Capacity Scaling Algorithm 2 3 4

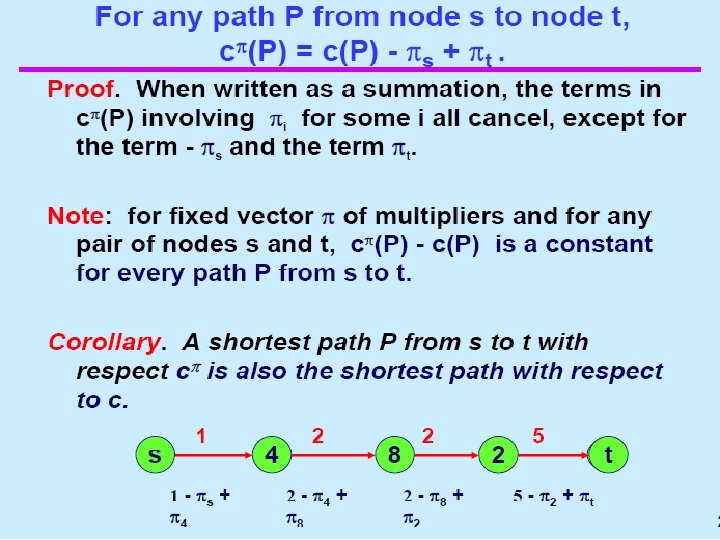
Reading The Capacity Scaling Algorithm

2

3

4

5

6

7

The Capacity Scaling Algorithm Animation

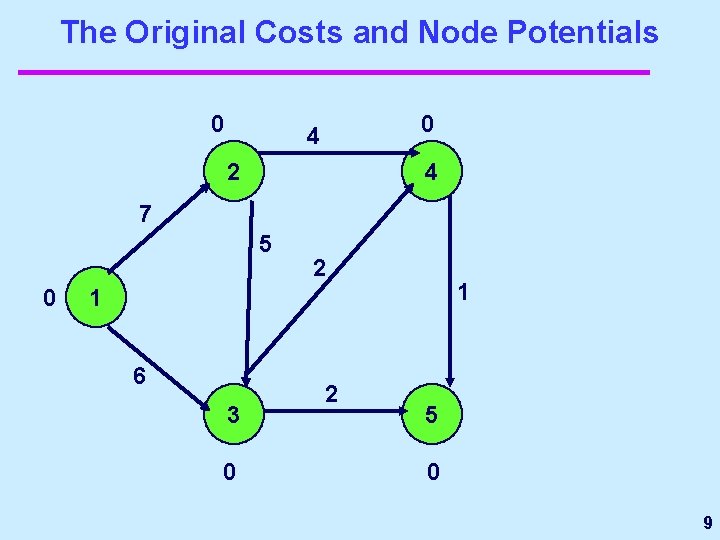
The Original Costs and Node Potentials 0 0 4 2 4 7 5 0 2 1 1 6 3 0 2 5 0 9

10

11

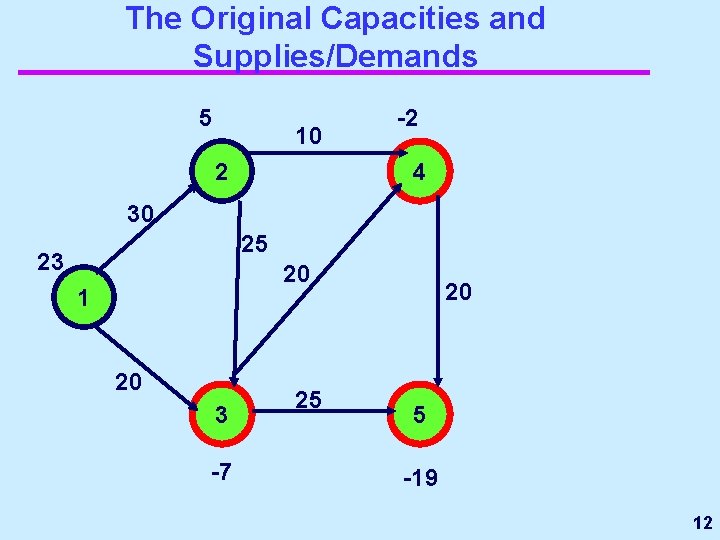
The Original Capacities and Supplies/Demands 5 10 2 -2 4 30 25 23 20 1 20 3 -7 25 20 5 -19 12

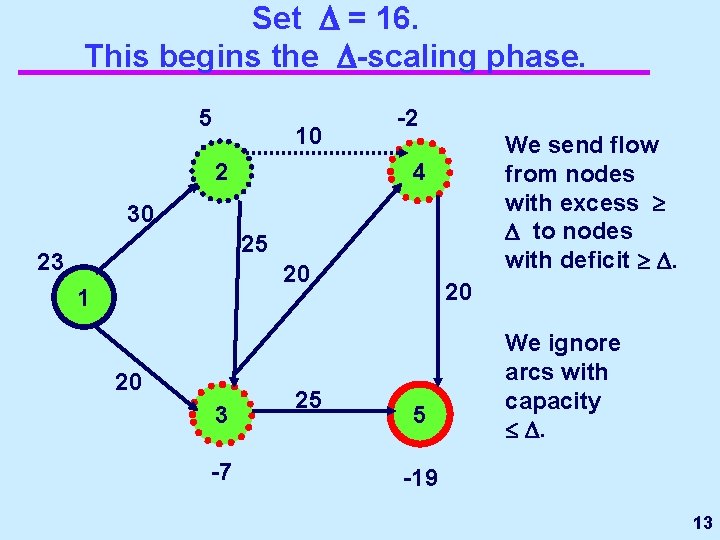
Set = 16. This begins the -scaling phase. 5 10 2 -2 We send flow from nodes with excess to nodes with deficit . 4 30 25 23 20 1 20 3 -7 25 20 5 We ignore arcs with capacity . -19 13

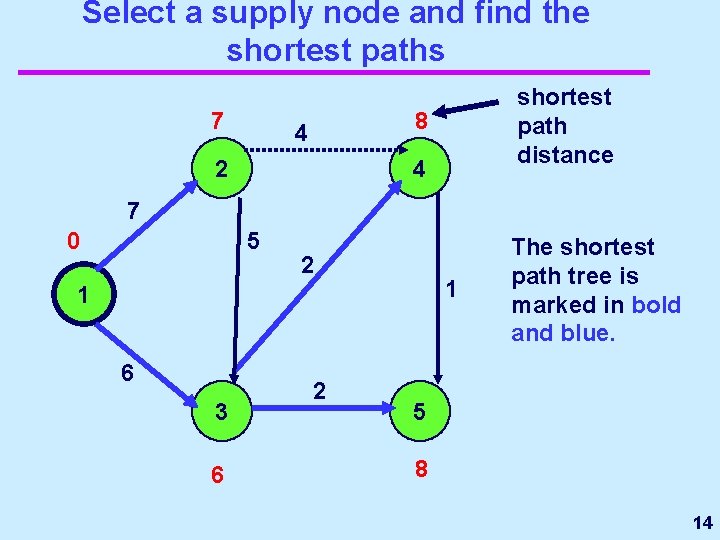
Select a supply node and find the shortest paths 7 shortest path distance 8 4 2 4 7 0 5 2 1 1 6 3 6 2 The shortest path tree is marked in bold and blue. 5 8 14

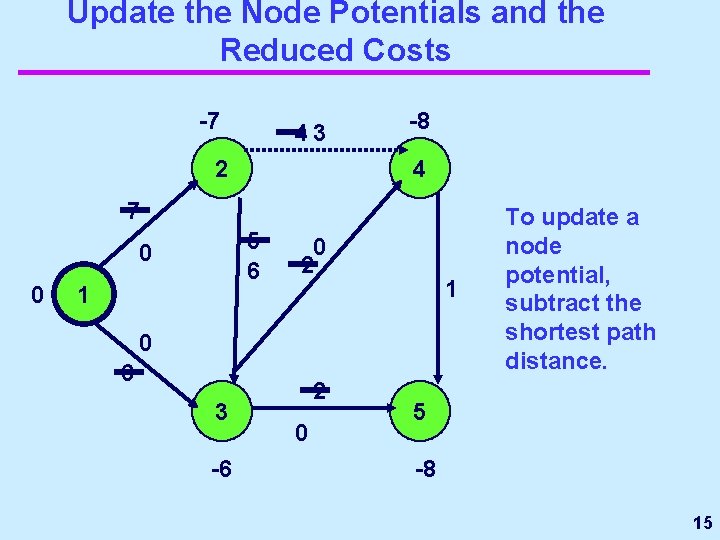
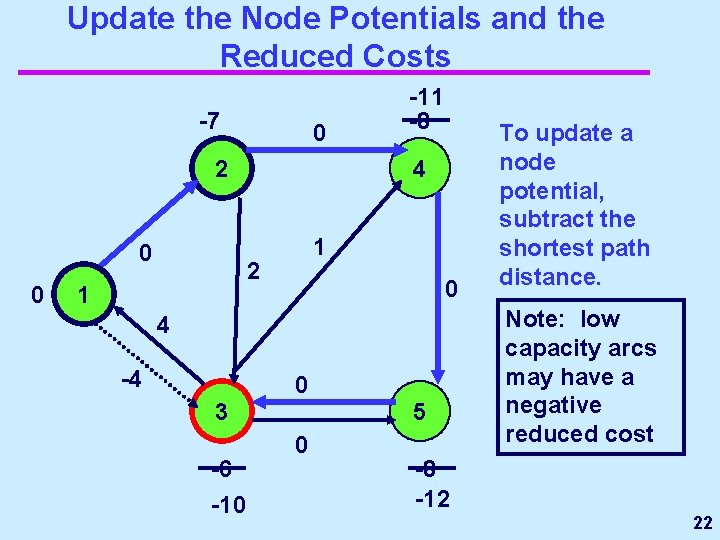
Update the Node Potentials and the Reduced Costs -7 43 2 -8 4 7 5 6 0 0 1 0 2 1 0 6 3 -6 2 0 To update a node potential, subtract the shortest path distance. 5 -8 15

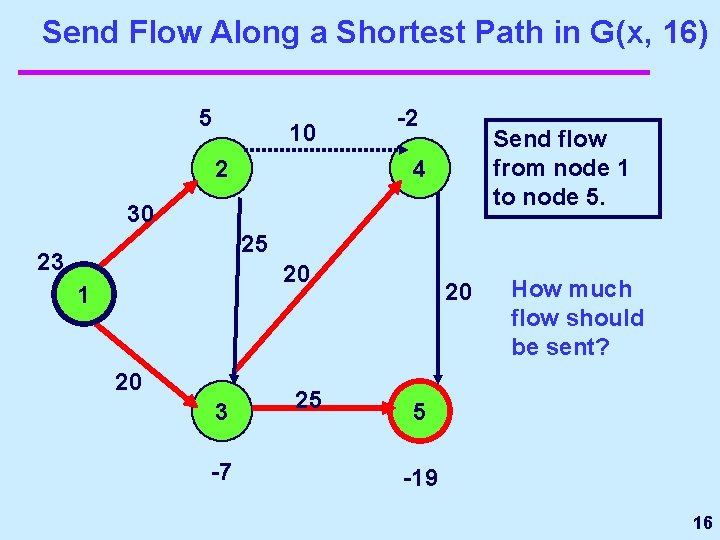
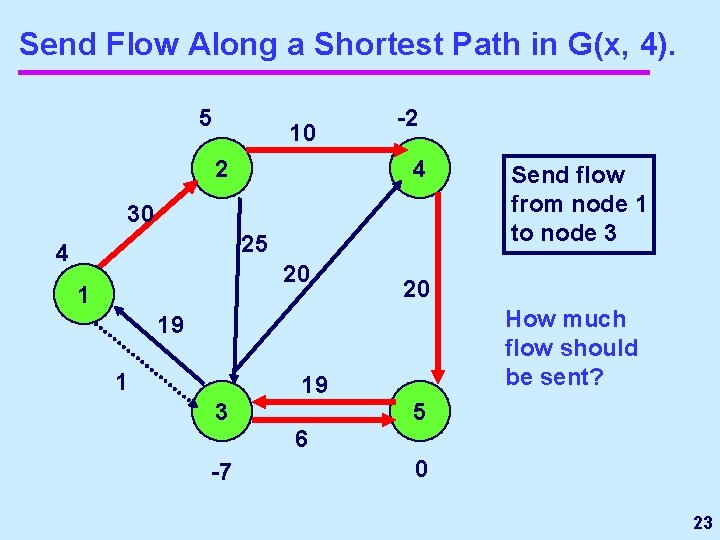
Send Flow Along a Shortest Path in G(x, 16) 5 10 2 -2 Send flow from node 1 to node 5. 4 30 25 23 20 1 20 3 -7 25 20 How much flow should be sent? 5 -19 16

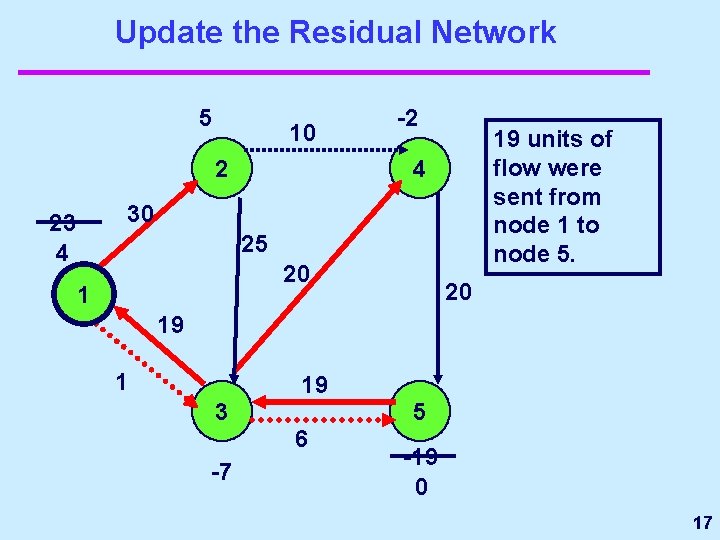
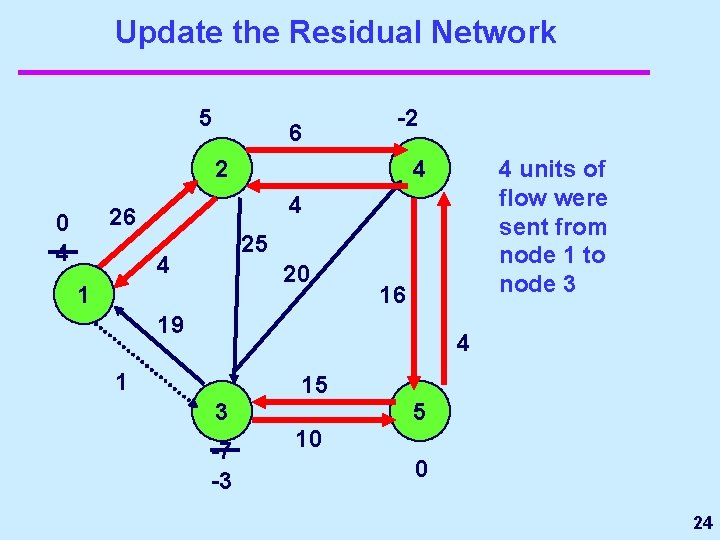
Update the Residual Network 5 10 2 -2 19 units of flow were sent from node 1 to node 5. 4 30 23 4 25 20 19 1 19 3 5 6 -7 -19 0 17

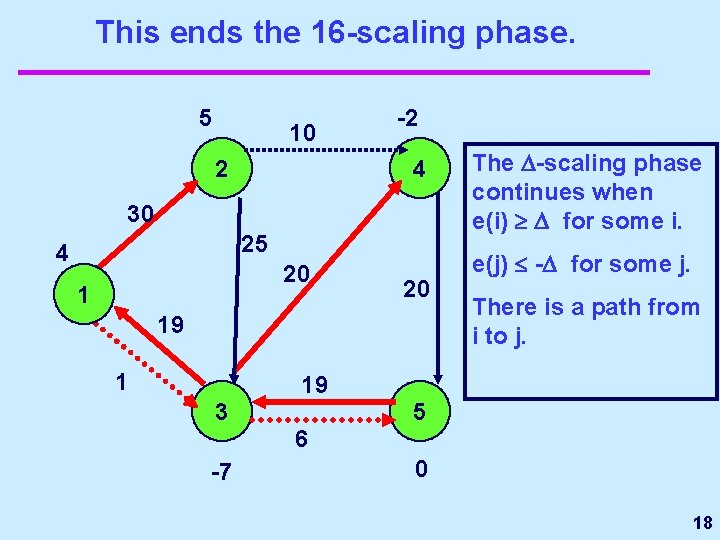
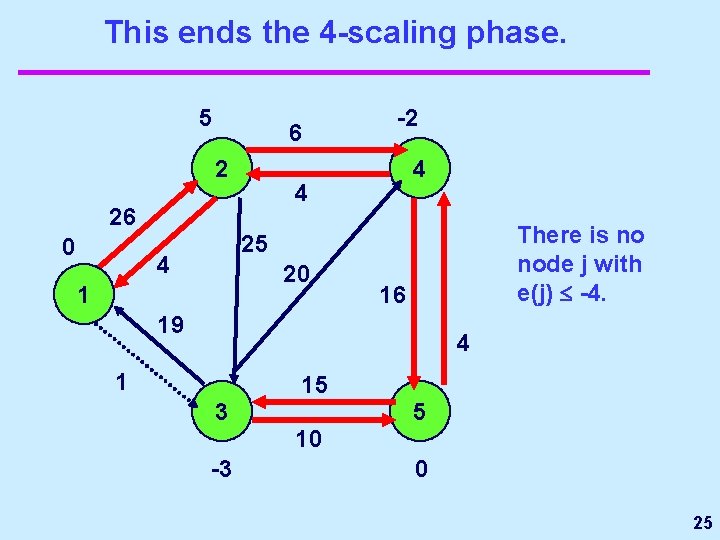
This ends the 16 -scaling phase. 5 10 2 -2 4 30 25 4 20 19 1 The -scaling phase continues when e(i) for some i. e(j) - for some j. There is a path from i to j. 19 3 5 6 -7 0 18

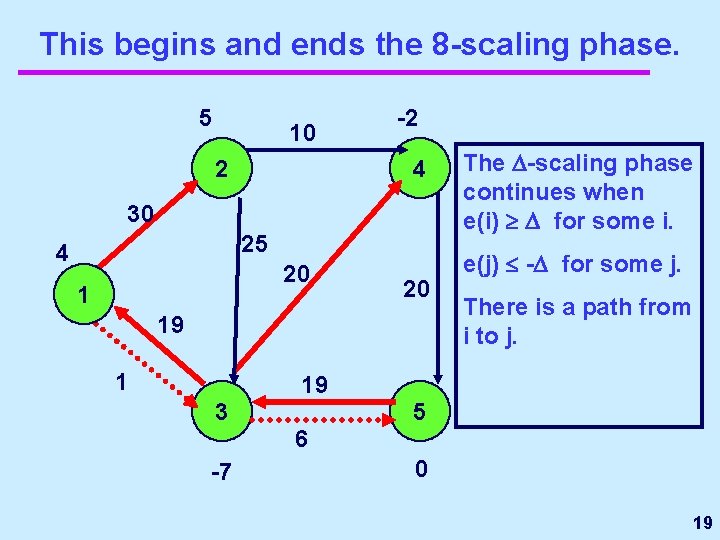
This begins and ends the 8 -scaling phase. 5 10 2 -2 4 30 25 4 20 19 1 The -scaling phase continues when e(i) for some i. e(j) - for some j. There is a path from i to j. 19 3 5 6 -7 0 19

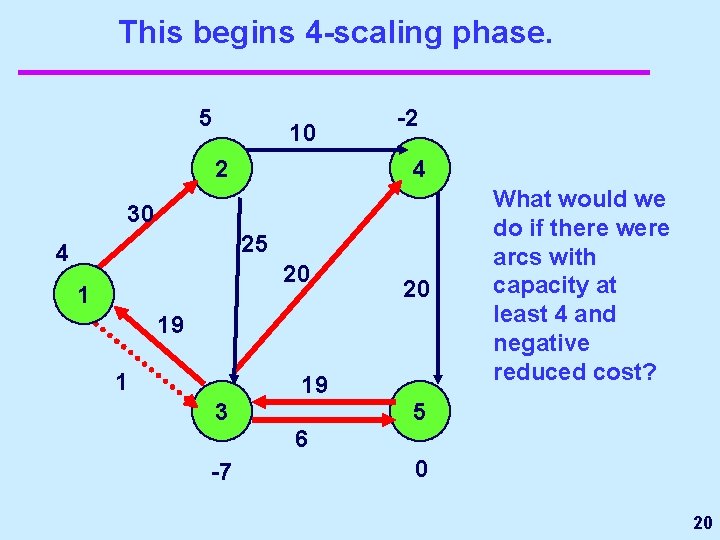
This begins 4 -scaling phase. 5 10 2 -2 4 30 25 4 20 19 1 19 3 What would we do if there were arcs with capacity at least 4 and negative reduced cost? 5 6 -7 0 20

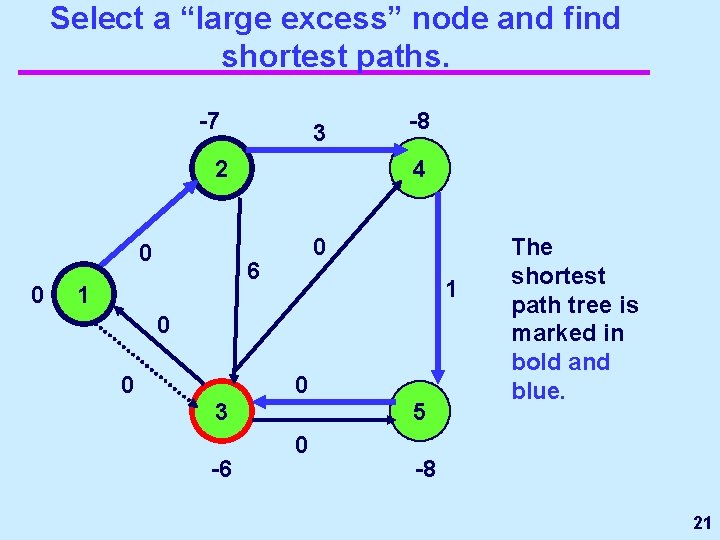
Select a “large excess” node and find shortest paths. -7 3 2 0 0 4 0 6 1 -8 1 0 0 0 3 -6 5 0 The shortest path tree is marked in bold and blue. -8 21

Update the Node Potentials and the Reduced Costs -7 0 2 0 0 4 1 2 1 -11 -8 0 4 -4 0 3 -6 -10 5 0 To update a node potential, subtract the shortest path distance. Note: low capacity arcs may have a negative reduced cost -8 -12 22

Send Flow Along a Shortest Path in G(x, 4). 5 10 2 -2 4 30 25 4 20 1 20 How much flow should be sent? 19 1 19 3 Send flow from node 1 to node 3 5 6 -7 0 23

Update the Residual Network 5 6 -2 2 4 4 26 0 4 4 units of flow were sent from node 1 to node 3 25 4 20 1 16 19 4 1 15 3 -7 -3 5 10 0 24

This ends the 4 -scaling phase. 5 6 2 4 4 26 0 -2 There is no node j with e(j) -4. 25 4 20 1 16 19 4 1 15 3 5 10 -3 0 25

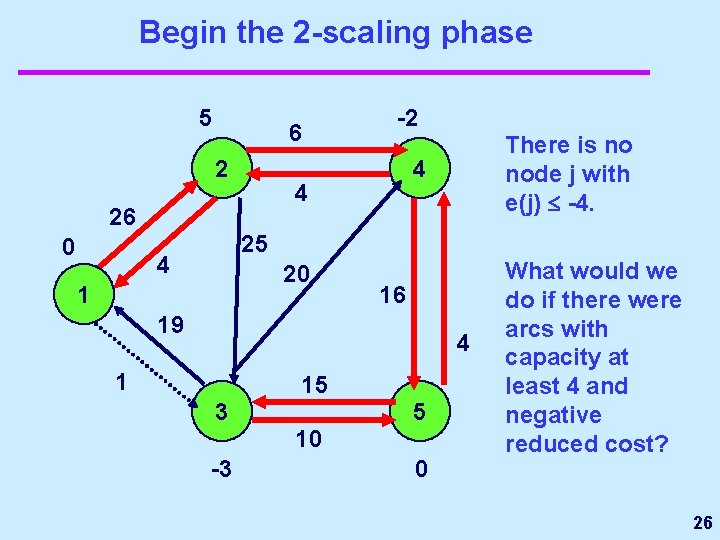
Begin the 2 -scaling phase 5 6 2 There is no node j with e(j) -4. 4 4 26 0 -2 25 4 20 1 16 19 4 1 15 3 5 10 -3 0 What would we do if there were arcs with capacity at least 4 and negative reduced cost? 26

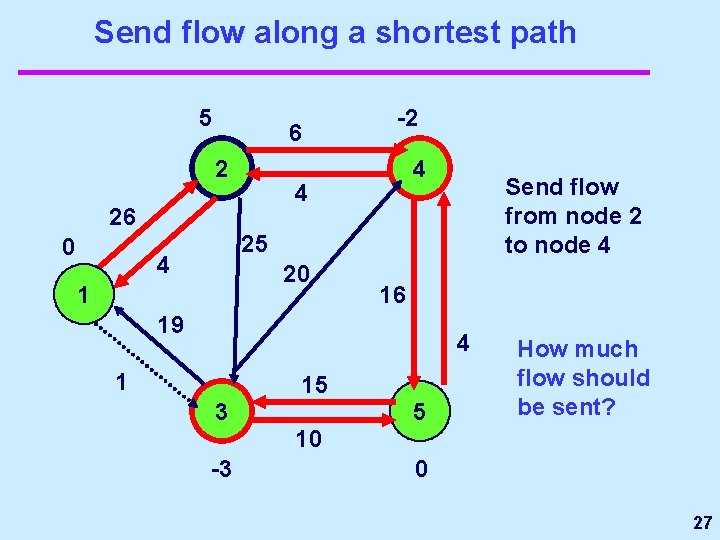
Send flow along a shortest path 5 6 2 4 4 26 0 -2 Send flow from node 2 to node 4 25 4 20 1 16 19 4 1 15 3 5 How much flow should be sent? 10 -3 0 27

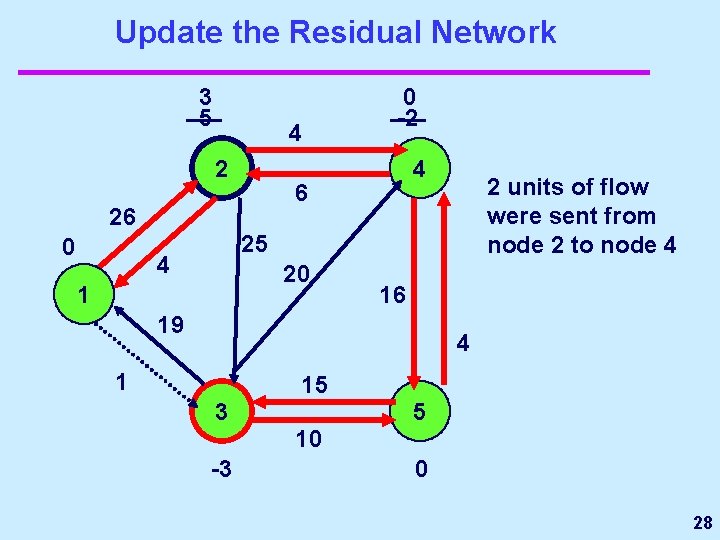
Update the Residual Network 3 5 4 2 4 6 26 0 0 -2 2 units of flow were sent from node 2 to node 4 25 4 20 1 16 19 4 1 15 3 5 10 -3 0 28

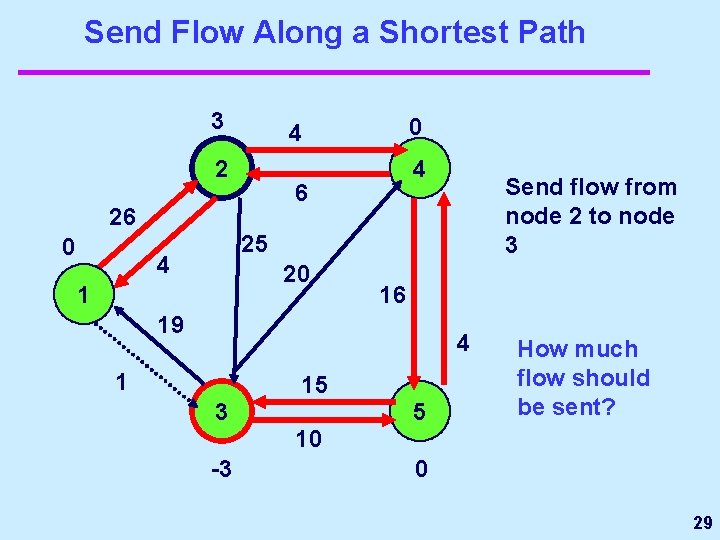
Send Flow Along a Shortest Path 3 2 4 6 26 0 0 4 Send flow from node 2 to node 3 25 4 20 1 16 19 4 1 15 3 5 How much flow should be sent? 10 -3 0 29

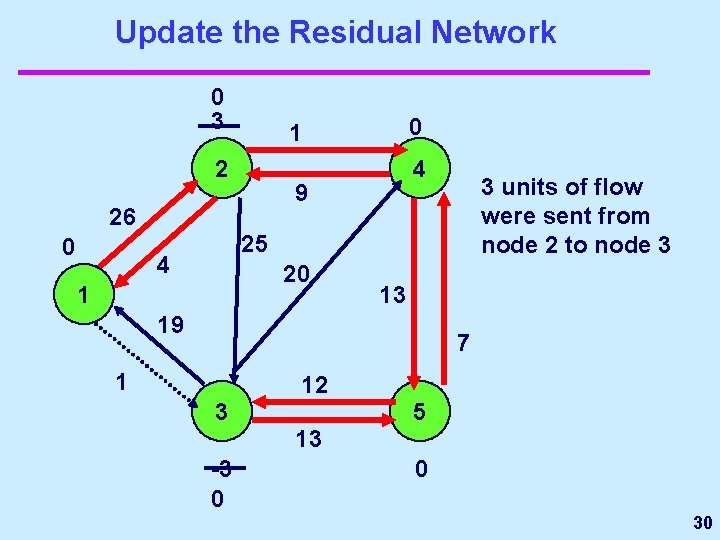
Update the Residual Network 0 3 2 4 9 26 0 0 1 3 units of flow were sent from node 2 to node 3 25 4 20 1 13 19 7 1 12 3 5 13 -3 0 0 30

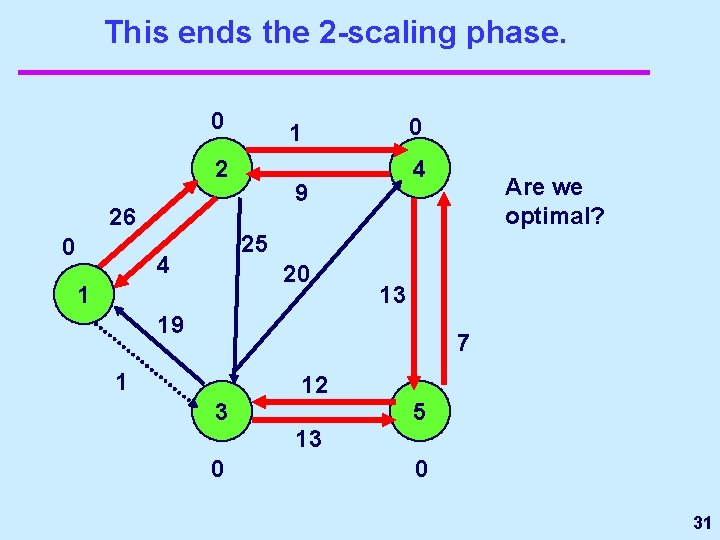
This ends the 2 -scaling phase. 0 2 4 9 26 0 0 1 Are we optimal? 25 4 20 1 13 19 7 1 12 3 5 13 0 0 31

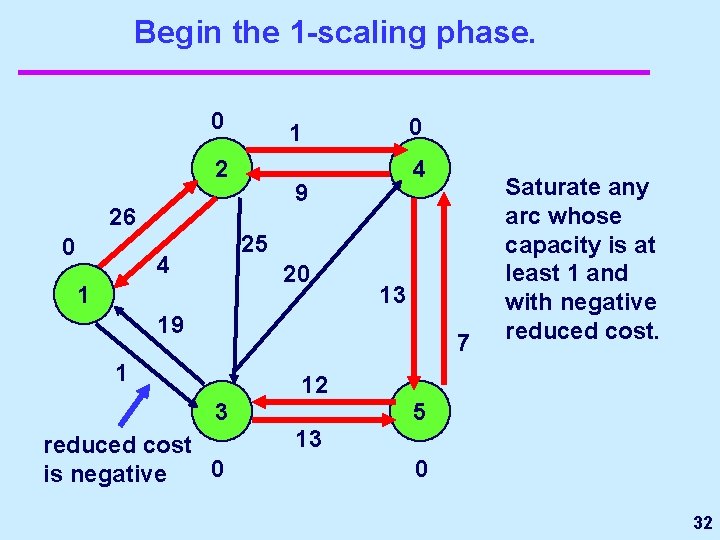
Begin the 1 -scaling phase. 0 2 4 9 26 0 0 1 25 4 20 1 13 19 7 1 Saturate any arc whose capacity is at least 1 and with negative reduced cost. 12 3 reduced cost 0 is negative 5 13 0 32

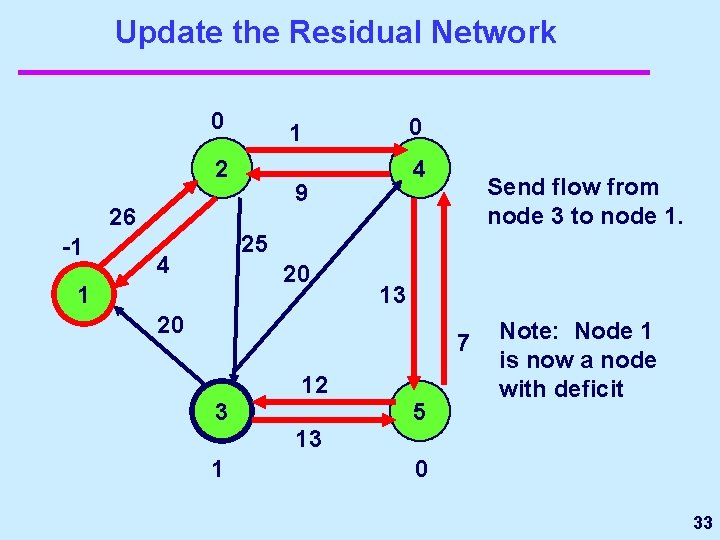
Update the Residual Network 0 2 4 9 26 -1 0 1 Send flow from node 3 to node 1. 25 4 20 1 13 20 7 12 3 5 Note: Node 1 is now a node with deficit 13 1 0 33

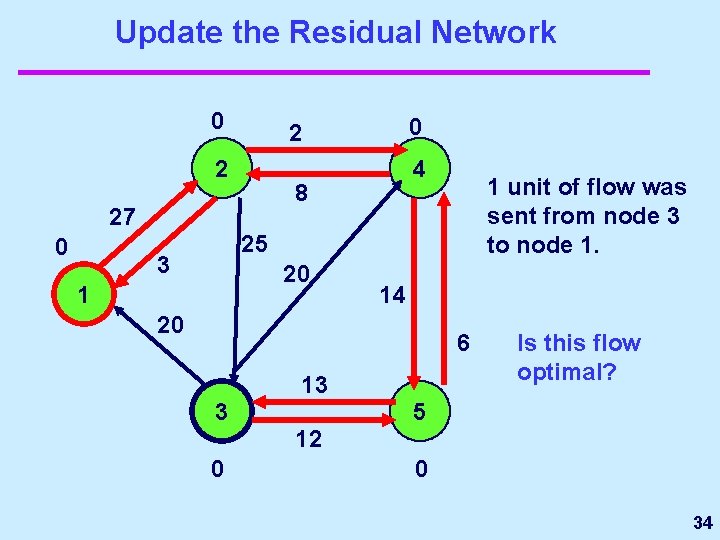
Update the Residual Network 0 2 4 8 27 0 0 2 1 unit of flow was sent from node 3 to node 1. 25 3 20 1 14 20 6 13 3 Is this flow optimal? 5 12 0 0 34

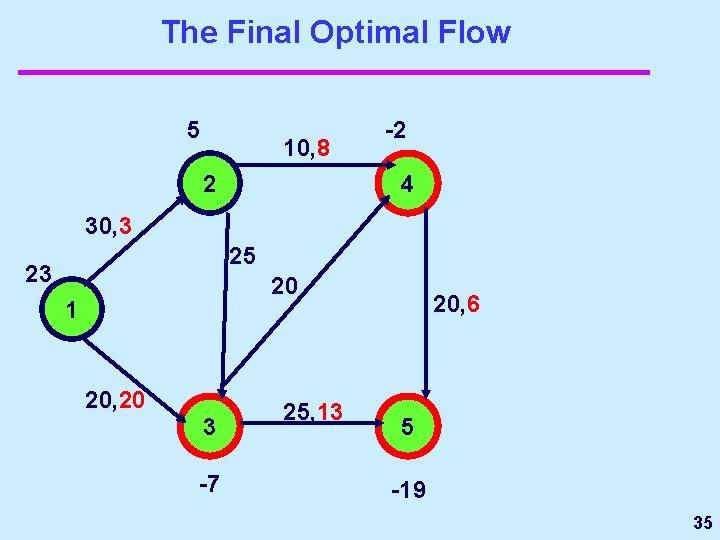
The Final Optimal Flow 5 10, 8 2 -2 4 30, 3 25 23 20 1 20, 20 3 -7 25, 13 20, 6 5 -19 35

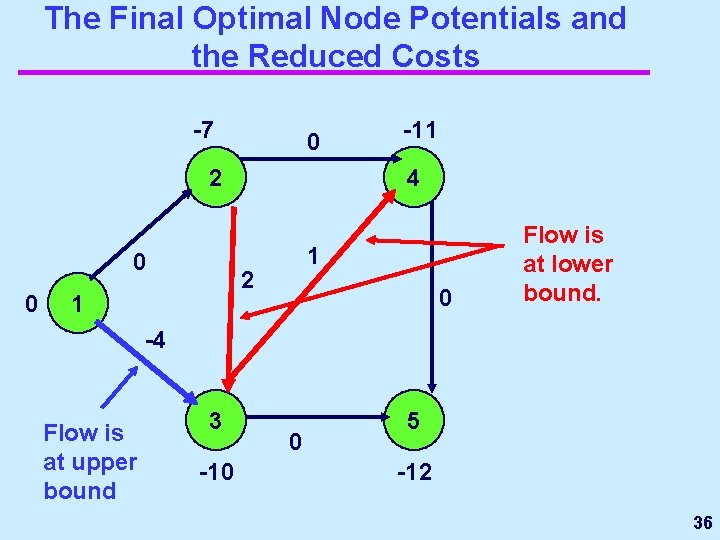
The Final Optimal Node Potentials and the Reduced Costs -7 0 2 0 0 4 1 2 1 -11 0 Flow is at lower bound. -4 Flow is at upper bound 3 -10 0 5 -12 36