Reaction Equilibrium in Ideal Gas Mixture 1 Subtopics

Reaction Equilibrium in Ideal Gas Mixture 1

Subtopics �Chemical Potential in an Ideal Gas Mixture. �Ideal-Gas Reaction Equilibrium �Temperature Dependence of the Equilibrium Constant �Ideal-Gas Equilibrium Calculations 2

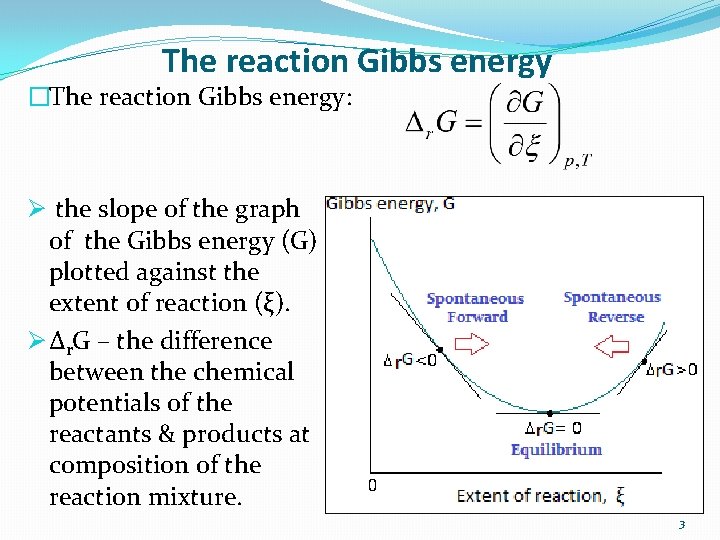
The reaction Gibbs energy �The reaction Gibbs energy: Ø the slope of the graph of the Gibbs energy (G) plotted against the extent of reaction (ξ). Ø Δr. G – the difference between the chemical potentials of the reactants & products at composition of the reaction mixture. the 3

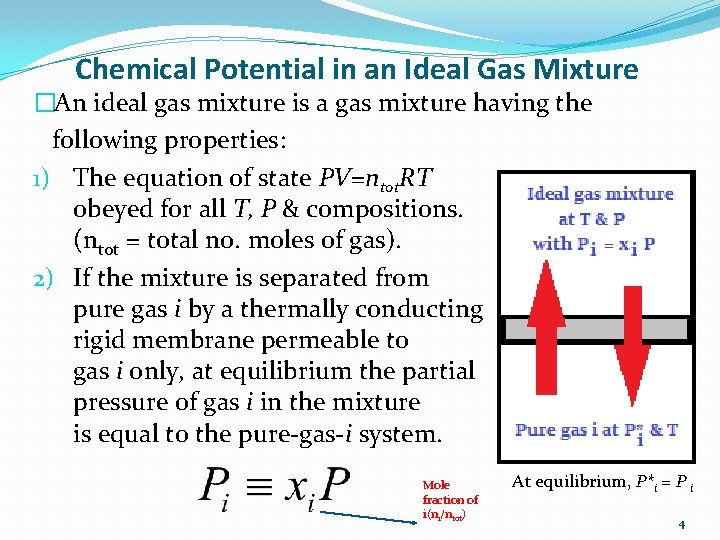
Chemical Potential in an Ideal Gas Mixture �An ideal gas mixture is a gas mixture having the following properties: 1) The equation of state PV=ntot. RT obeyed for all T, P & compositions. (ntot = total no. moles of gas). 2) If the mixture is separated from pure gas i by a thermally conducting rigid membrane permeable to gas i only, at equilibrium the partial pressure of gas i in the mixture is equal to the pure-gas-i system. Mole fraction of i(ni/ntot) At equilibrium, P*i = P i 4

Chemical Potential in an Ideal Gas Mixture �Let μi – the chemical potential of gas i in the mixture �Let μ*i – the chemical potential of the pure gas in equilibrium with the mixture through the membrane. �The condition for phase equilibrium: �The mixture is at T & P, has mole fractions x 1, x 2, …. xi �The pure gas i is at temp, T & pressure, P*i. �In an ideal gas mixture, P*i at equilibrium equals to the partial pressure of i in the mixture. �For ideal gas mixture, 5

Chemical Potential in an Ideal Gas Mixture �From chemical potential of a pure ideal gas: (for standard state, ) �For a ideal gas mixture: 6

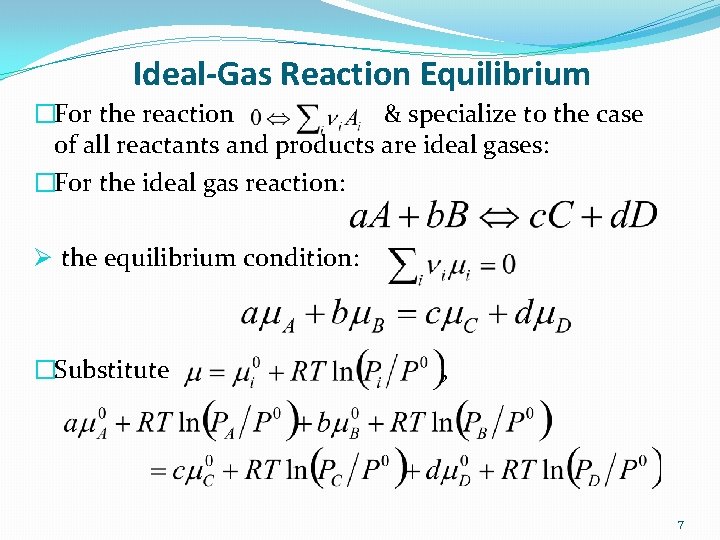
Ideal-Gas Reaction Equilibrium �For the reaction & specialize to the case of all reactants and products are ideal gases: �For the ideal gas reaction: Ø the equilibrium condition: �Substitute , 7

Ideal-Gas Reaction Equilibrium �The equilibrium condition becomes: Ø where eq – emphasize that there are partial pressure at equilibrium. 8

Ideal-Gas Reaction Equilibrium �Defining the standard equilibrium constant (K 0 p) for the ideal gas reaction: a. A + b. B c. C + d. D �Then, 9

Ideal-Gas Reaction Equilibrium �For the general ideal-gas reaction: �Repeat the derivation above, �Then, �Define: �Then, �Standard equilibrium constant: (Standard pressure equilibrium constant) 10

Ideal-Gas Reaction Equilibrium �A chemical system which has reached the reversible thermodynamic state shows no further net reaction. Since Ø This does not mean that nothing is occurring. Ø Actually, the chemical reactions in both directions continue, but at the same rate. Ø The result is no net change in concentrations, but there is still a lot going on chemically. 11

Example 1 �A mixture of 11. 02 mmol of H 2 S & 5. 48 mmol of CH 4 was placed in an empty container along with a Pt catalyst & the equilibrium was established at 7000 C & 762 torr. �The reaction mixture was removed from the catalyst & rapidly cooled to room temperature, where the rates of the forward & reverse reactions are negligible. �Analysis of the equilibrium mixture found 0. 711 mmol of CS 2. �Find & for the reaction at 700 0 C. 12

Temperature Dependence of the Equilibrium Constant �The ideal-gas equilibrium constant (Kp 0) is a function of temperature only. Ø It is independent of P, V, # of the reaction species �Differentiation with respect to T: �From 13

Temperature Dependence of the Equilibrium Constant �Since , Ø This is the Van’t Hoff equation. Ø The greater the | ΔH 0 |, the faster Kp 0 changes with temperature. �Integration: �Neglect the temperature dependence of ΔH 0, 14

Example 2 �Find Kp 0 at 600 K for the reaction by using the approximation that ΔH 0 is independent of T; Note: Substance k. J/mol NO 2 (g) 33. 18 51. 31 N 2 O 4 (g) 9. 16 97. 89 15

Temperature Dependence of the Equilibrium Constant �Since , the van’t Hoff equation can be: Ø The slope of a graph of ln. Kp 0 vs 1/T at a particular temperature equals –ΔH 0/R at that temperature. Ø If ΔH 0 is essentially constant over the temperature range, the graph of ln. Kp 0 vs 1/T is a straight line. �The graph is useful to find ΔH 0 if Δf. H 0 of all the species are not known. 16

Example 3 �Use the plot ln. Kp 0 vs 1/T for temperature in the range of 200 to 1000 K 25 ln. Kp 0 0 �Estimate the ΔH. 20 15 10 5 0 -5 0 0. 001 0. 002 0. 003 0. 004 0. 005 T -1 /K -1 -10 -15 -20 Plot of ln. Kp 0 vs 1/T 17

Ideal-Gas Equilibrium Calculations �Thermodynamics enables us to find the Kp 0 for a reaction without making any measurements on an equilibrium mixture. Ø Kp 0 - obvious value in finding the maximum yield of product in a chemical reaction. Ø If ΔGT 0 is highly positive for a reaction, this reaction will not be useful for producing the desired product. Ø If ΔGT 0 is negative or only slightly positive, the reaction may be useful. �A reaction with a negative ΔGT 0 is found to proceed extremely slow - + catalyst 18

Ideal-Gas Equilibrium Calculations �The equilibrium composition of an ideal gas reaction mixture is a function of : Ø T and P (or T and V). Ø the initial composition (mole numbers) n 1, 0, n 2, 0…. . Of the mixture. �The equilibrium composition is related to the initial composition by the equilibrium extent of reaction (ξeq). �Our aim is to find ξeq. 19

Ideal-Gas Equilibrium Calculations Specific steps to find the equilibrium composition of an ideal-gas reaction mixture: 1) Calculate ΔGT 0 of the reaction using and a table of Δf. GT 0 values. 2) Calculate Kp 0 using [If Δf. GT 0 data at T of the reaction are unavailable, Kp 0 at T can be estimated using which assume ΔH 0 is constant] 20

Ideal-Gas Equilibrium Calculations 3) Use the stoichiometry of the reaction to express the equilibrium mole numbers (ni) in terms of the initial mole number (ni, 0) & the equilibrium extent of reaction (ξeq), according to ni=n 0+νi ξeq. 4) (a) If the reaction is run at fixed T & P, use (if P is known) & the expression for ni from ni=n 0+νi ξeq to express each equilibrium partial pressure Pi in term of ξeq. (b) If the reaction is run at fixed T & V, use Pi=ni. RT/V (if V is known) to express each Pi in terms of ξeq 21

Ideal-Gas Equilibrium Calculations 5) Substitute the Pi’s (as function of ξeq) into the equilibrium constant expression & solve ξeq. 6) Calculate the equilibrium mole numbers from ξeq and the expressions for ni in step 3. 22

Example 4 �Suppose that a system initially contains 0. 300 mol of N 2 O 4 (g) and 0. 500 mol of NO 2 (g) & the equilibrium is attained at 250 C and 2. 00 atm. �Find the equilibrium composition. �Note: Substance k. J/mol NO 2 (g) 33. 18 51. 31 N 2 O 4 (g) 9. 16 97. 89 23

Example 5 �Kp 0 =6. 51 at 800 K for the ideal gas reaction: �If 3. 000 mol of A, 1. 000 mol of B and 4. 000 mol of C are placed in an 8000 cm 3 vessel at 800 K. �Find the equilibrium amounts of all species. 24

Le Chatelier’s Principle �The statement of Le Chatelier’s principle is generally if a system at equilibrium is stressed, the reaction will shift to relieve that stress. �Chemical reactions can be exposed to stresses including a change in temperature, a change in pressure, a change in concentration of one or more of the participants and others. (1) Effect of changes in temperature: ØThe effect of an increase in temperature of a system at equilibrium is a shift in the direction which absorbs heat. 25

Le Chatelier’s Principle (2) Effect of changes in pressure: Ø When the pressure of a system at equilibrium increases, the reaction occurs in the direction that lowers the pressure by reducing the volume of gas. (3) Effect of varying the concentration: Ø Increasing the concentration of any component of a system at equilibrium will cause a shift resulting in using up some of the added substance. (4) Effect of catalysts: Ø Catalysts accelerate both forward & reverse reaction rates equally. Ø Catalysts can be used to shorten the amount of time it takes to reach equilibrium when the original concentrations do not match equilibrium concentration. 26

Answer (Example 1) �Mole fraction: �P = 762 torr, �Partial pressure: �Standard pressure, P 0 = 1 bar =750 torr. 27

Answer (Example 1) �Use �At 7000 C (973 K), 28

Answer (Example 2) �If ΔH 0 is independent of T, then the van’t Hoff equation gives �From 29

Answer (Example 3) �T-1 = 0. 0040 K-1, ln. Kp 0 = 20. 0. �T-1 = 0. 0022 K-1, ln. Kp 0 = 0. 0. �The slope: �From �So, 30

Answer (Example 4) �Get: �From �By the stoichiometry, 31

Answer (Example 4) �Since T & P are fixed: �Use 32

Answer (Example 4) �The reaction occurs at: P=2. 00 atm=1520 torr & P 0=1 bar=750 torr. �Clearing the fractions: �Use quadratic formula: �So, x = -0. 324 @ -0. 176 Ø Number of moles of each substance present at equilibrium must be positive. Ø Thus, Ø So, Ø As a result, 33

Answer (Example 5) �Let x moles of B react to reach equilibrium, at the equilibrium: �The reaction is run at constant T and V. �Using Pi=ni. RT/V & substituting into �We get: �Substitute P 0=1 bar=750. 06 torr, R=82. 06 cm 3 atm mol-1 K-1, 34

Answer (Example 5) �We get, �By using trial and error approach, solve the cubic 35 equation. �The requirements: n. B>0 & n. D>0, Hence, 0 < x <1. �Guess if x=0, the left hand side = -2. 250 �Guess if x =1, the left hand side = 0. 024 �Guess if x=0. 9, the left hand side = -0. 015 �Therefore, 0. 9 < x < 1. 0. �For x=0. 94, the left hand side = 0. 003 �For x=0. 93, the left hand side=-0. 001 �As a result, n. A=1. 14 mol, n. B=0. 07 mol, n. C=4. 93 mol, n. D=0. 93 mol.