Reaction Engineering Batch culture exponential phase balanced growth

Reaction Engineering

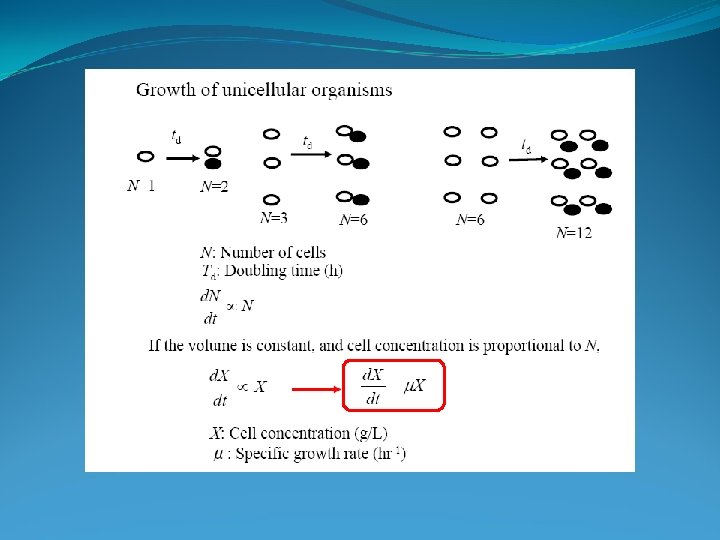
Batch culture: exponential phase (balanced growth) Exponential phase = log-phase Maximum growth rates μmax „midexponential“: bacteria often used for functional studies Max growth rate -> smallest doubling time

Michaelis Menten Kinetics • Used when microbe population is constant = non-growing (or short time spans) • Derivable from first principles (enzyme-substrate binding rates and equilibria expressions) • Parameter determination methods used for Monod calculations (i. e. Lineweaver Burke)

Monod Growth Kinetics • Relates specific growth rate, m, to substrate concentration • Empirical---no theoretical basis—it just “fits”! • Have to determine mmax and Ks in the lab • Each m is determined for a different starting S

Michaelis Menten vs. Monod Michaelis Menten § Kinetic expression derived (theoretical) § Constant enzyme pool § § Free enzymes Non-growing microbes § v vs. S where v is velocity § Km is half saturation constant Monod Empirical expression Growth Enzyme concentration increases with time Relates microbial growth rate constant to S μ vs S Ks is half saturation constant

Michaelis Menten vs. Monod § Parameters (vmax or μmax; Ks or Km) are determined by linearization (e. g. Lineweaver Burke model) or nonlinear curve fitting. § Relationship between dependent variable and S determined experimentally, in the lab §Range of S §Set conditions (T, chemistry, enzyme or microbe) §Measure the v or μ for each S §Plot v or μ vs. S; analyze data for parameter estimation

Determining Monod parameters • Double reciprocal plot (Lineweaver Burke) • Commonly used • Caution that data spread are often insufficient • Other linearization (Eadie Hofstee) • Less used, better data spread • Non-linear curve fitting • More computationally intensive • Progress-curve analysis (for substrate depletion) • Less lab work (1 curve), more uncertainty

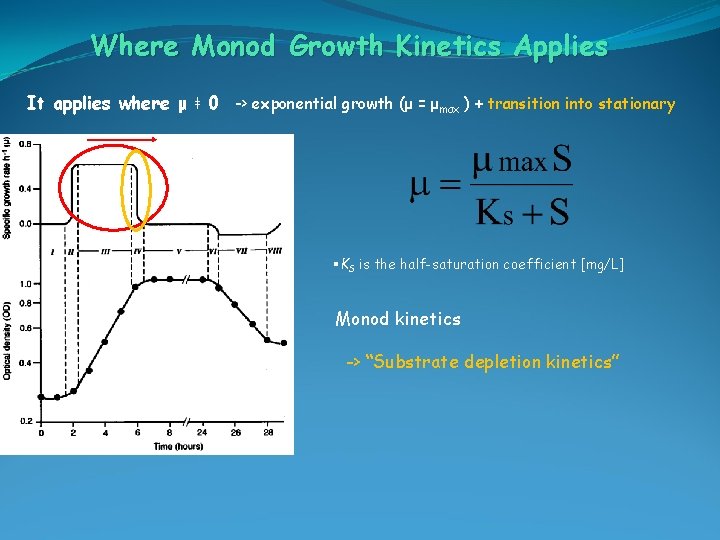
Where Monod Growth Kinetics Applies It applies where μ ǂ 0 -> exponential growth (μ = μmax ) + transition into stationary §KS is the half-saturation coefficient [mg/L] Monod kinetics -> “Substrate depletion kinetics”

Substrate Depletion Kinetics Since Y Yield coefficients And Monod applies!! Then And Where k = §k is the maximum substrate utilization rate [sec-1] § KS is the half-saturation coefficient [mg/L]

Substrate Depletion Kinetics § Substrate consumption rates have often been described using ‘Monod kinetics’ -> Substrate controls growth Kinetics § S is the substrate concentration [mg/L] § X is the biomass concentration [mg/ L] § k is the maximum substrate utilization rate [sec-1] § KS is the half-saturation coefficient [mg/L]

Stoichiometric Coefficients for Growth Yield coefficients, Y, are defined based on the amount of consumption of another material. Because ΔS changes with growth condition, YX/S is not a constant

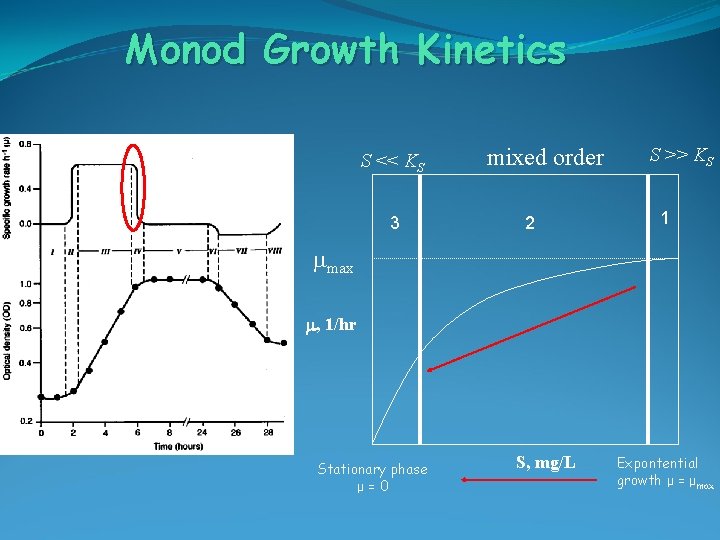
Monod Growth Kinetics S << KS 3 mixed order 2 S >> KS 1 mmax m, 1/hr Stationary phase μ=0 S, mg/L Expontential growth μ = μmax

Depletion Kinetics 1. Zero-order region, S >> KS, the equation can be approximated by μ = μmax -> exponential growth S << KS 2. Center region, Monod “mixed order” kinetics must be used -> transition from exponential growth to stationary growth caused by [S] limitation 3 mixed order 2 mmax 3. First-order region, S << KS, the equation can be approximated as μ = μmax. S/Ks -> transition from exponential growth to stationary growth caused by [S] limitation Just before stationary phase starts (stationary phase μ = 0) §k is the maximum substrate utilization rate [sec -1] § KS is the half-saturation coefficient [mg/L] m, 1/hr S, mg/L S >> KS 1

Modeling Substrate Depletion §Three common assumptions § Monod kinetics applies (mid range concentrations) -> “Substrate depletion kinetics” § First-order decay (low concentration of S, applicable to many natural systems) § Zero-order decay (substrate saturated) μ =μmax -> exponential growth

Growth and Production Kinetic §Cellular growth rate §Monod approximation §Yield factor §Substrate Utilization §Product Formation § (Beginning of Stationary Phase)

Factors Determining Kinetics §Rate per microbe, which depends on §Species §Substrates §Environmental factors §Total numbers of microbes

Quantification of Microbes in the Environment • Culture-based (limited: 2000 species vs. 13, 000 species of bacteria in soil by DNA-based methods • Counting colony forming units (CFUs) • Activity assays: need cell or biomass count to normalize • Culture-independent • Direct Counts • General fluorescent stain, like acridine orange or SYBR gold • Counting cells in FISH assay • Biomass assays • Quantification of an element like C or N • Chloroform fumigation / incubation or direct extraction • Total protein or DNA

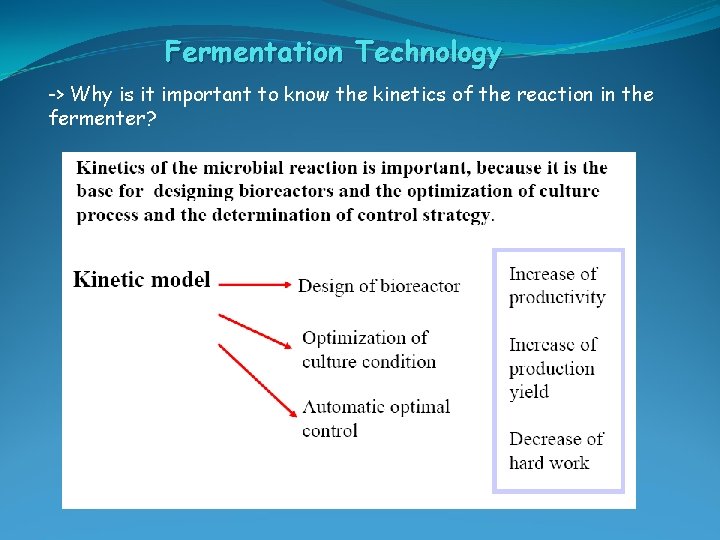
Fermentation Technology -> Why is it important to know the kinetics of the reaction in the fermenter?

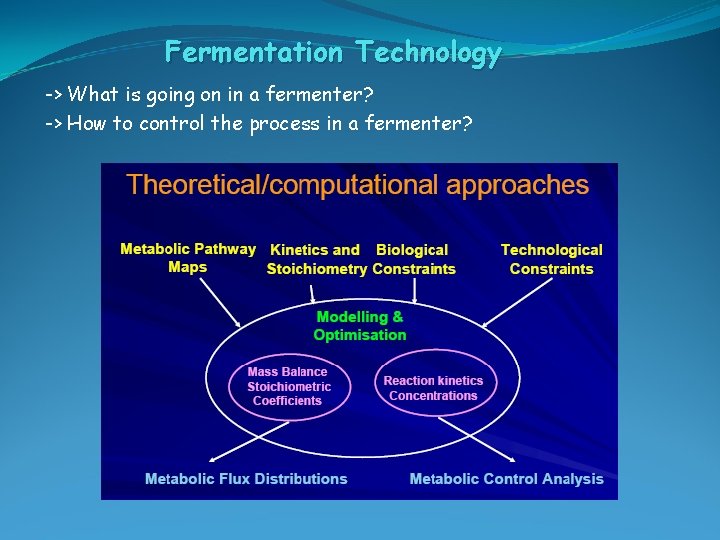
Fermentation Technology -> What is going on in a fermenter? -> How to control the process in a fermenter?

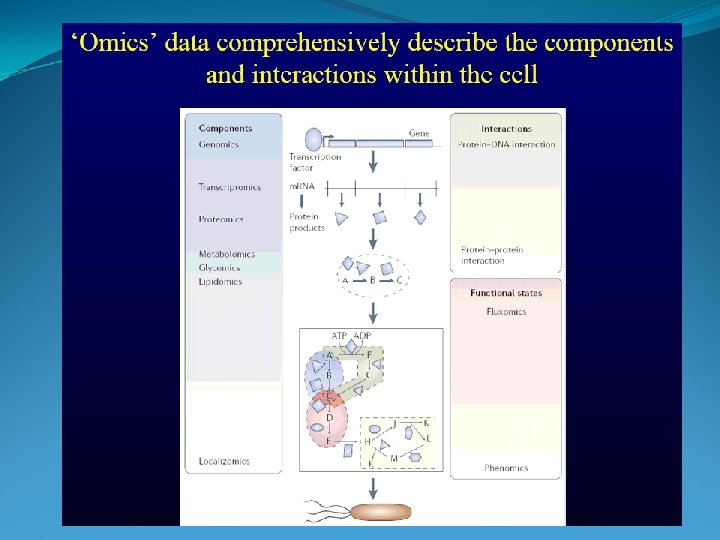
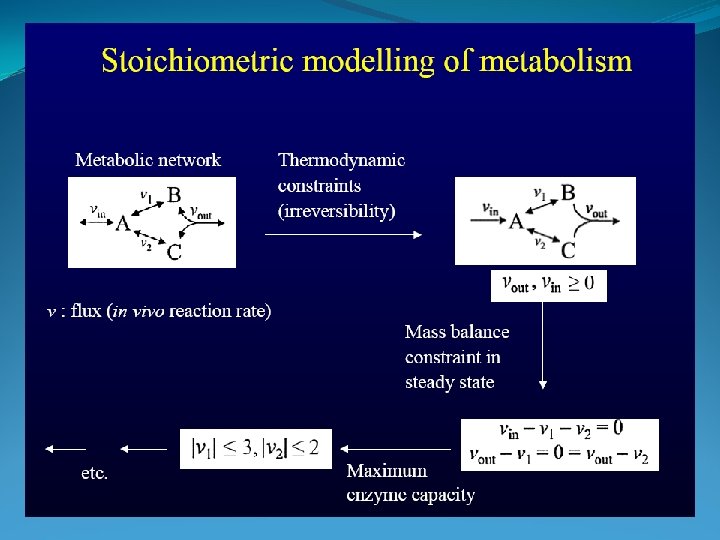
Stochiometric Coefficients

Mass Balance

Example -> Too complex !!!!

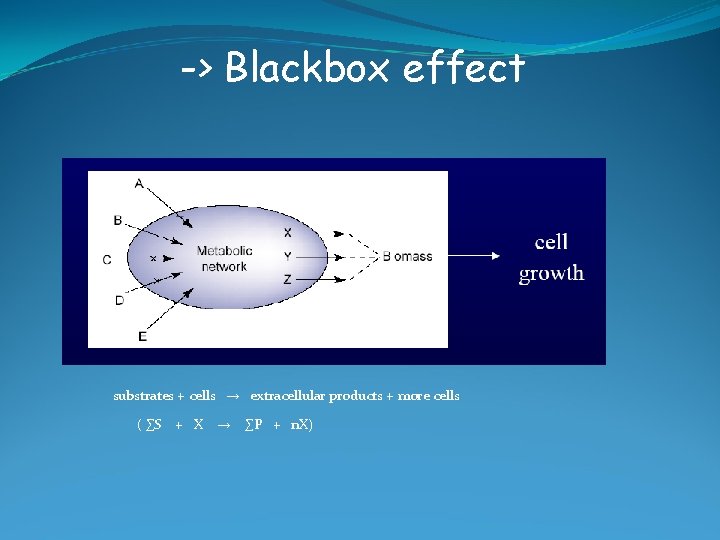
-> Blackbox effect substrates + cells → extracellular products + more cells ( ∑S + X → ∑P + n. X)

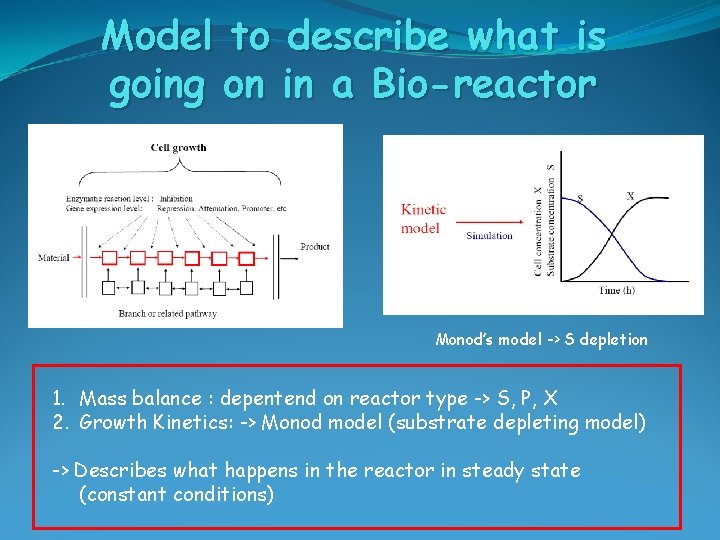
Model to describe what is going on in a Bio-reactor Monod’s model -> S depletion 1. Mass balance : depentend on reactor type -> S, P, X 2. Growth Kinetics: -> Monod model (substrate depleting model) -> Describes what happens in the reactor in steady state (constant conditions)

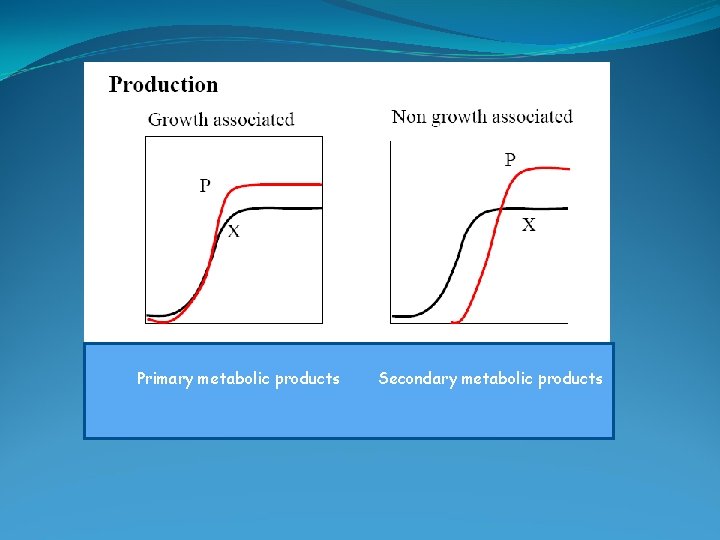
Primary metabolic products Secondary metabolic products

Microbial Products 1. Growth associated products : products appear simultaneoulsy with cells in culture qp is the specific rate of product formation (mg product per g biomas per hours 2. Non-growth associated products : products appear during stationary phase of batch growth 3. Mixed-growth associated products : products appear during slow growth and stationary phase

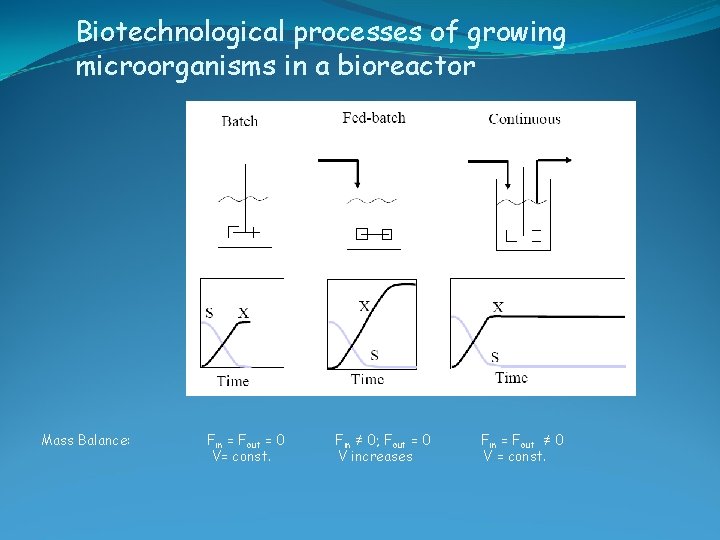
Biotechnological processes of growing microorganisms in a bioreactor Mass Balance: Fin = Fout = 0 V= const. Fin ≠ 0; Fout = 0 V increases Fin = Fout ≠ 0 V = const.

Model to describe what is going on in a Bio-reactor 1. Mass balance : depentend on reactor type -> S, P, X 2. Growth Kinetics: -> Monod model (substrate depleting model) -> Describes what happens in the reactor in steady state (constant conditions) 1. Mass Ballance: In – Out + Reaction = Accumulation Biomass: FX 0 - FX + r V = dn/dt r = d. X/dt = µ X 2. Monod Kinetics: 3. Steady state: d. X/dt = 0 (NOT for Batch reactor!!!) dn/dt = d(XV)/dt

Batch Reactor Closed Well-mixed Constant volume -> substrate growth limiting factor CV Mass Balance: Verbal: Acc = dn/dt In – Out + Reaction = Accumulation Math: 0 0 Rearrange: r. V d. X/dt V r V = d. X/dt V n = mole dn/dt = d(XV)/dt = d. X/dt V Growth -> Substrate concentration controls growth rate Growth

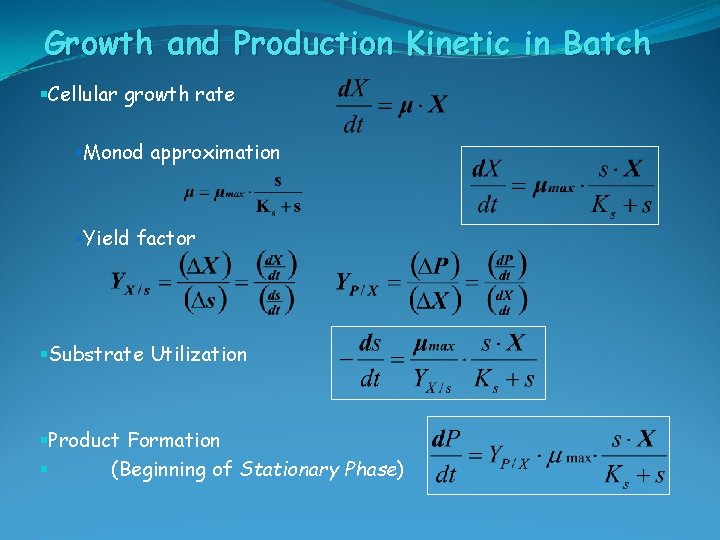
Growth and Production Kinetic in Batch §Cellular growth rate §Monod approximation §Yield factor §Substrate Utilization §Product Formation § (Beginning of Stationary Phase)

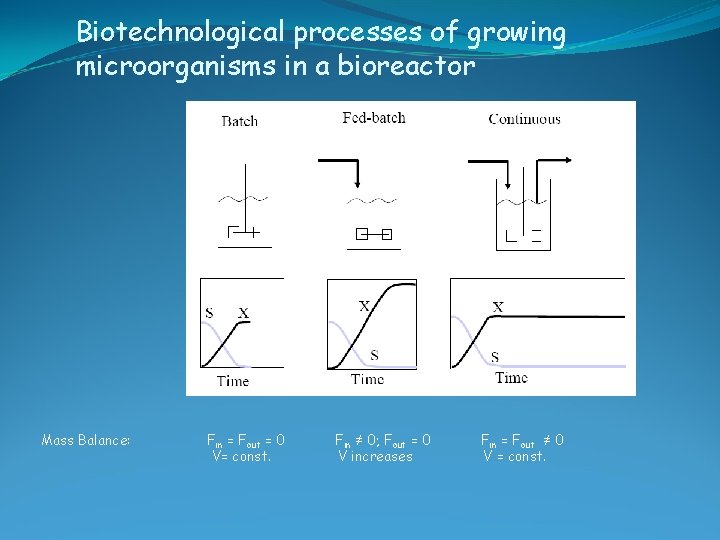
Biotechnological processes of growing microorganisms in a bioreactor Mass Balance: Fin = Fout = 0 V= const. Fin ≠ 0; Fout = 0 V increases Fin = Fout ≠ 0 V = const.