Reaction Diffusion Models of Biological Pattern Formation The

Reaction Diffusion Models of Biological Pattern Formation: The Effects of Domain Growth and Time Delays EA Gaffney Collaborators: NAM Monk, E Crampin, PK Maini

Summary of Background In 1952 Turing proposed that – Pattern Formation during morphogenesis might arise through an instability in systems of reacting chemicals (morphogens), which is driven by diffusion. – Heterogeneous concentrations of these chemicals form a “pre-pattern”. Subsequent differentiation of tissue/cell type is in response to whether or not one of these morphogens exceeds some threshold locally. – The equations describing this for two reacting constituents on a stationary domain are of the form

In the simplest setting there is a unique homogeneous steady state at (a 0, b 0), given by solutions of The Jacobean at the stationary point is of the form The kinetics are always chosen such that, in the absence of diffusion, the homogeneous steady state is stable (and thus the instability is diffusion driven) In the presence of diffusion, for a sufficiently large domain, and quite reasonably assuming the components of the Jacobean are O(1) compared to the scales ε, 1/ε the homogeneous steady state is unstable if

For • a domain larger than the critical size, again assuming the components of the Jacobean are O(1) compared to the scales ε , 1/ε • ε <<1 sufficiently small the rate of growth of the fastest growing mode, μ, is given by where

A key feature of all Turing-Pair kinetics is • Morphogen induced production of morphogen • Short range activation, long range inhibition. A specific example: Schnakenberg Kinetics p = 0. 9, q = 0. 1, ε << 1. 1/[T 0 ] = λ is the decay rate of the activator, b In particular the activator production is equivalent to a law of mass action rule

Potential Examples • Avian feather bud formation • HS Jung, …, L Wolpert, . . . et al, Developmental Biology 1998 • Vertebrate limb formation • CM Leonard et al, Developmental Biology, 1991. • TGF-β 2 possible activator; inhibitor undetermined • Zebrafish mesendoderm induction • • • L Solnica-Kreznel, Current Biology, 2003 Nodal (Squint) gene product is an activator. Lefty gene product is an inhibitor Evidence that range of Lefty's influence exceeds Nodal's. Molecular details remain to be uncovered of their interaction (though progress is rapid on this point) • Molecular details remain to be determined on the differential in their range of influence.

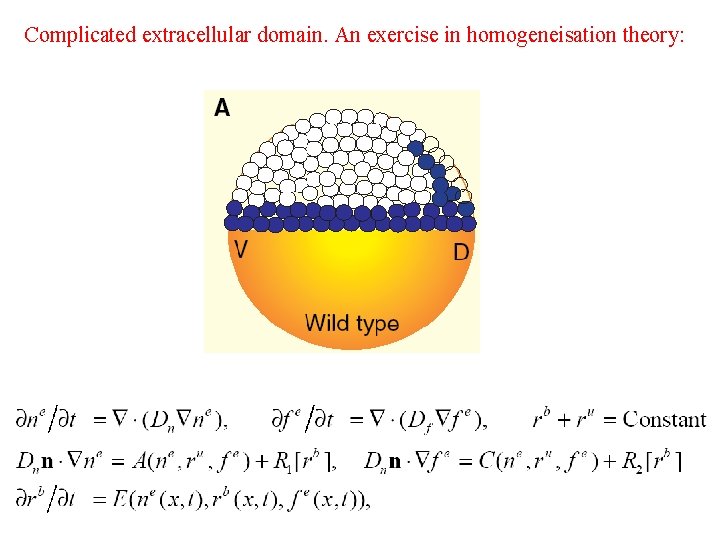
Difficulties • Reaction Diffusion Patterns can be observed to be very sensitive to – Noise (in initial conditions and generally). – Perturbations of the domain shape. • Turing Morphogens are hard to find. – However, more and more molecular data is being produced in developmental studies. These indicate that a possible Turing Pair are Nodal and Lefty in Zebrafish mesendodermal induction. • The molecular data also indicates that Nodal and Lefty and other putative Turing pairs induce each others' production by signal transduction and gene expression. – For example, in situ hybridisation reveals m. RNA transcripts of the proteins speculated to be Turing pairs. • The extracellular domain is complicated and tortuous. • The precise details of the kinetic functions are only ever speculated.

Formulating a model … Complicated extracellular domain
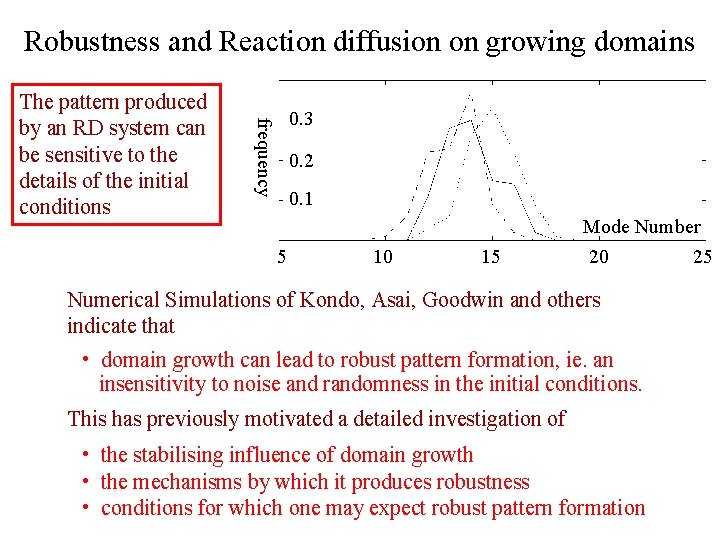
Robustness and Reaction diffusion on growing domains 0. 3 frequency The pattern produced by an RD system can be sensitive to the details of the initial conditions 0. 2 0. 1 5 10 15 Mode Number 20 25 Numerical Simulations of Kondo, Asai, Goodwin and others indicate that • domain growth can lead to robust pattern formation, ie. an insensitivity to noise and randomness in the initial conditions. This has previously motivated a detailed investigation of • the stabilising influence of domain growth • the mechanisms by which it produces robustness • conditions for which one may expect robust pattern formation

Model Formulation: Incorporating uniform domain growth Uniform growth Rescaling gives
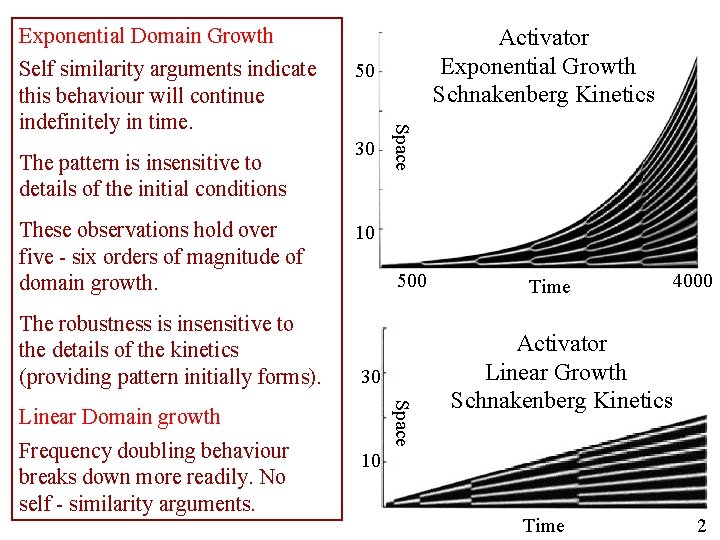
Exponential Domain Growth The pattern is insensitive to details of the initial conditions These observations hold over five - six orders of magnitude of domain growth. The robustness is insensitive to the details of the kinetics (providing pattern initially forms). 50 30 10 500 30 Space Linear Domain growth Frequency doubling behaviour breaks down more readily. No self - similarity arguments. Space Self similarity arguments indicate this behaviour will continue indefinitely in time. Activator Exponential Growth Schnakenberg Kinetics Time 4000 Activator Linear Growth Schnakenberg Kinetics 10 Time 2
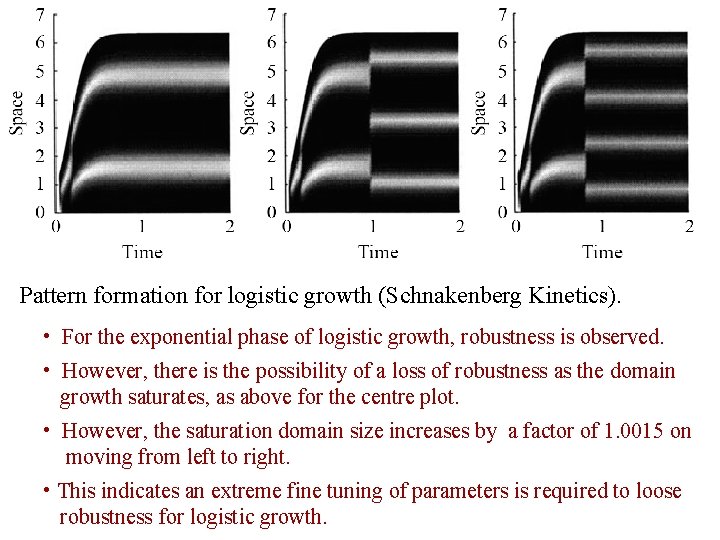
Pattern formation for logistic growth (Schnakenberg Kinetics). • For the exponential phase of logistic growth, robustness is observed. • However, there is the possibility of a loss of robustness as the domain growth saturates, as above for the centre plot. • However, the saturation domain size increases by a factor of 1. 0015 on moving from left to right. • This indicates an extreme fine tuning of parameters is required to loose robustness for logistic growth.

Conclusions: Robustness and Domain Growth Including GROWTH in 1 D reaction diffusion models leads to • Robustness to noise in the initial conditions over 4 -5 orders of magnitude of the growth rate for exponential growth • Semi-scale invariance. No need for parameter fine tuning or feedback between the domain size and the kinetics. • Persistence of robustness for logistic saturating growth. • Robustness independent of the exact details of the model providing pattern initially forms. Dismissal of Reaction Diffusion as a Pattern Formation mechanism on the grounds of robustness not necessarily founded if slow domain growth is relevant.

Time Delays
Question: How are the effects of signal transduction and gene expression time delays incorporated into a model? Signal
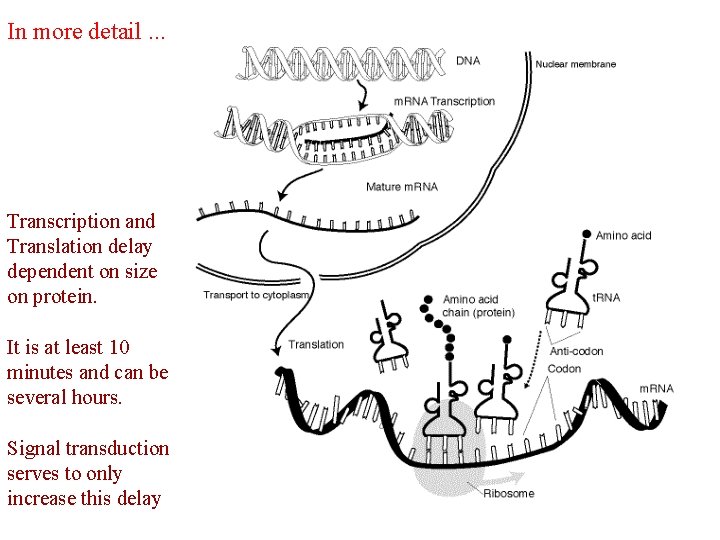
In more detail. . . Transcription and Translation delay dependent on size on protein. It is at least 10 minutes and can be several hours. Signal transduction serves to only increase this delay

For a suitable non-dimensionalisation, the Schnakenberg reaction diffusion equations, in the presence of domain growth and time delays, can be written in the form A, 2 B lost from reaction at time t 3 B gained from reaction at time t-τ u is the velocity field of the domain growth y takes values in [0, L(t)], where L(t) is the (non-dimensionalised) domain length τ is the gene expression time delay where


Model Investigations Linear Analysis. (a*, b*) is the homogeneous steady state solution Substitute into the model equations to obtain (on neglecting O(η 2)) –

In the absence of a time delay, with or without domain growth, substitute into • The critical value of the domain length is given via Schnakenberg Kinetics = • There are no oscillations at this critical point, nor for the fastest growing mode (at least providing ε 2 is sufficiently small). • The rate of growth of the fastest growing mode, μ, is again given by

In the absence of domain growth, substitute into + to obtain For ε <<1 sufficiently small and q 11 = q 12 = 0, q 22 > 0, p 22+q 22 > 0, as with Schnakenberg kinetics, one has • There are no oscillations at the critical domain length • The critical length for the onset of instability is unchanged by the time delay

In the absence of domain growth, substitute into + to obtain For ε <<1 sufficiently small and q 11 = q 12 = 0, q 22 > 0, p 22+q 22 > 0, as with Schnakenberg kinetics, one has • Writing λ = μ + iν, the rate of growth of the fastest growing mode, μ, is given implicitly by
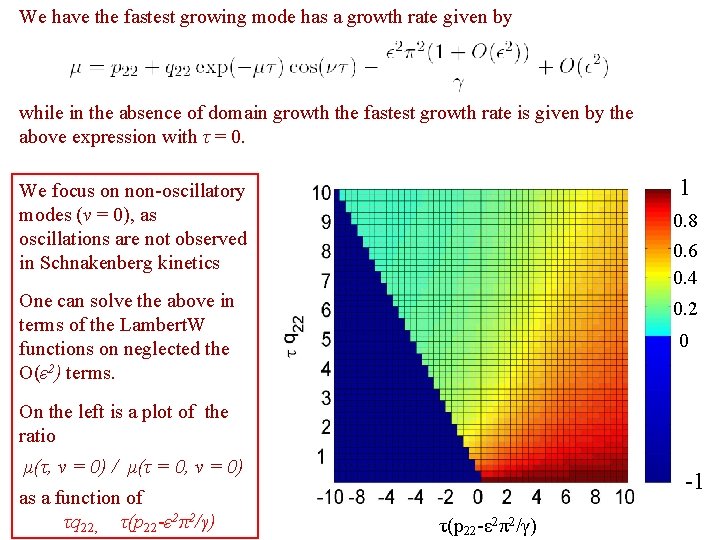
We have the fastest growing mode has a growth rate given by while in the absence of domain growth the fastest growth rate is given by the above expression with τ = 0. 1 We focus on non-oscillatory modes (ν = 0), as oscillations are not observed in Schnakenberg kinetics 0. 8 0. 6 0. 4 One can solve the above in terms of the Lambert. W functions on neglected the O(ε 2) terms. 0. 2 0 On the left is a plot of the ratio μ(τ, ν = 0) / μ(τ = 0, ν = 0) as a function of τq 22, τ(p 22 -ε 2π2/γ) -1 τ(p 22 -ε 2π2/γ)
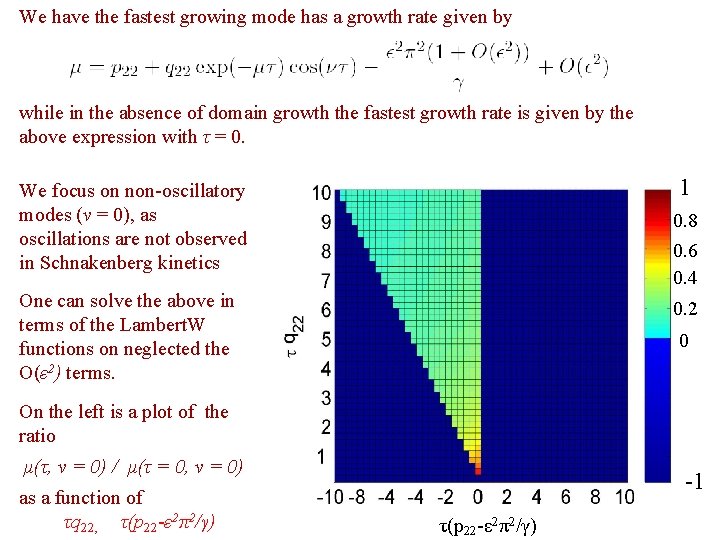
We have the fastest growing mode has a growth rate given by while in the absence of domain growth the fastest growth rate is given by the above expression with τ = 0. 1 We focus on non-oscillatory modes (ν = 0), as oscillations are not observed in Schnakenberg kinetics 0. 8 0. 6 0. 4 One can solve the above in terms of the Lambert. W functions on neglected the O(ε 2) terms. 0. 2 0 On the left is a plot of the ratio μ(τ, ν = 0) / μ(τ = 0, ν = 0) as a function of τq 22, τ(p 22 -ε 2π2/γ) -1 τ(p 22 -ε 2π2/γ)

Explicitly Solving the Linear Equations to obtain insight for when there are both Time delays and Domain Growth
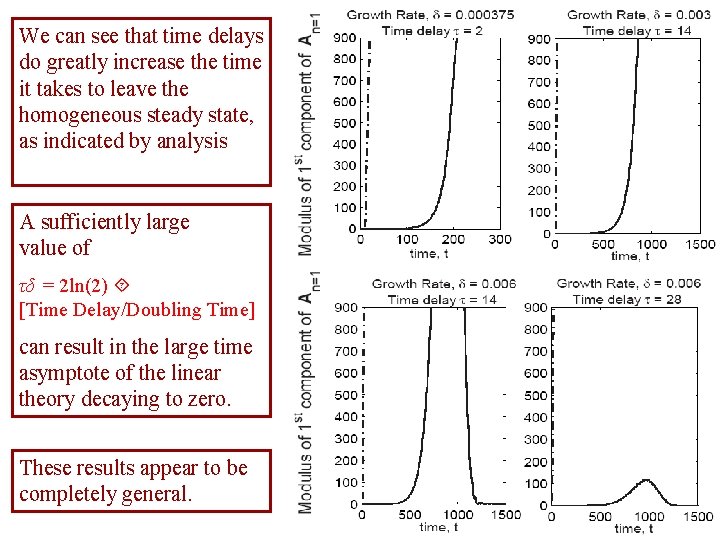
We can see that time delays do greatly increase the time it takes to leave the homogeneous steady state, as indicated by analysis A sufficiently large value of τδ = 2 ln(2) [Time Delay/Doubling Time] can result in the large time asymptote of the linear theory decaying to zero. These results appear to be completely general.
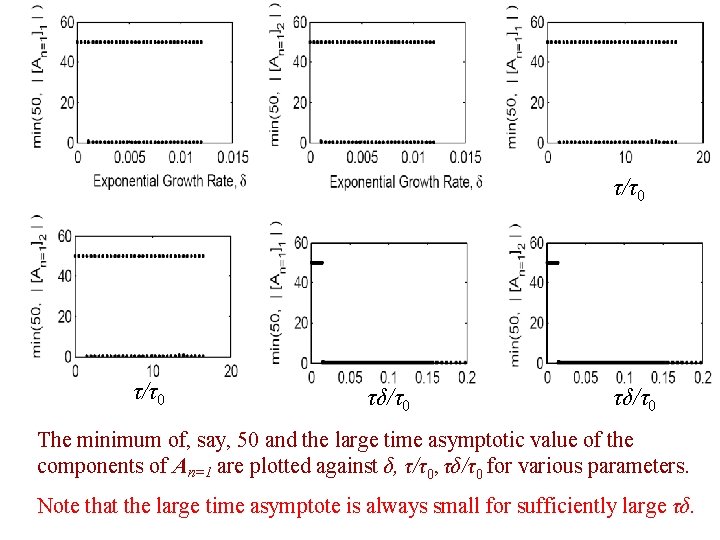
τ/τ0 τδ/τ0 The minimum of, say, 50 and the large time asymptotic value of the components of An=1 are plotted against δ, τ/τ0, τδ/τ0 for various parameters. Note that the large time asymptote is always small for sufficiently large τδ.
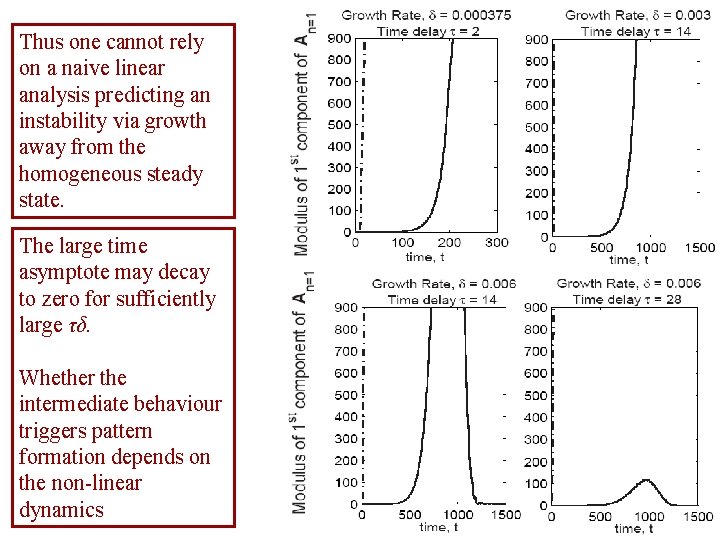
Thus one cannot rely on a naive linear analysis predicting an instability via growth away from the homogeneous steady state. The large time asymptote may decay to zero for sufficiently large τδ. Whether the intermediate behaviour triggers pattern formation depends on the non-linear dynamics

Conclusions from the linearised equations • Domain Growth, No Time Delay. In the absence of time delays, domain growth does not have much effect on the linear analysis • Time delays, No Domain Growth. There will typically be a substantial patterning lag – The location of the onset of the instability is independent of the time delay – The ratio of the fastest growing modes in the presence of the time and in the absence of the time delay will typically be large. • Domain Growth & Time Delays. – There will typically be a substantial patterning lag – A naive linear analysis is conceptually flawed for the prediction of instability. Whether the intermediate behaviour triggers pattern formation depends on the non-linear dynamics – The behaviour of the large asymptote is governed by the parameter τδ = 2 ln(2) [Time Delay/Doubling Time]

Numerical Simulations of the Nonlinear equations with Schankenberg kinetics and domain growth and time delays
![Initial Conditions for t in the domain [0, τ]: a b x x The Initial Conditions for t in the domain [0, τ]: a b x x The](http://slidetodoc.com/presentation_image_h2/dc45d4a34ed2c573339ceec82ea3ca29/image-31.jpg)
Initial Conditions for t in the domain [0, τ]: a b x x The initial conditions are typically given by the solid lines above (IC=1) and the dashed lines (IC=2). We also consider multiplying these initial conditions by time dependent factors. One example is [1+ 0. 0025 cos (πx) cos (πt/(2τ))] All the behaviour observed below is representative of the numerous initial conditions considered. Similarly for an order of magnitude variation of the parameters τ, ε, δ.
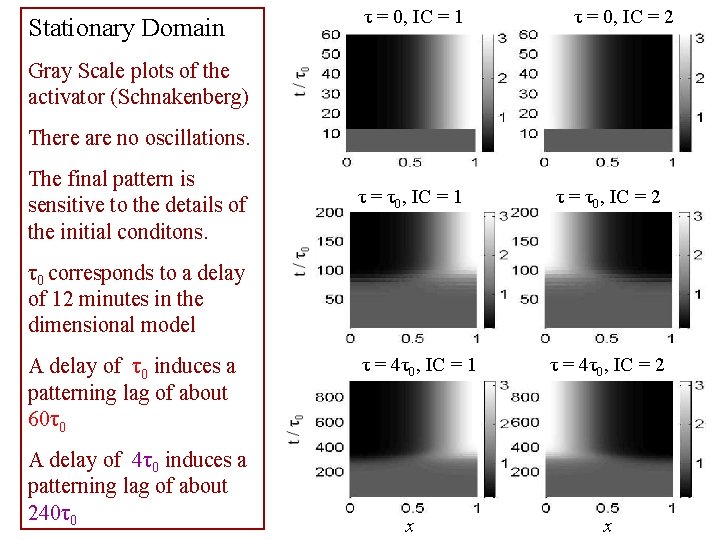
Stationary Domain τ = 0, IC = 1 τ = 0, IC = 2 Gray Scale plots of the activator (Schnakenberg) There are no oscillations. The final pattern is sensitive to the details of the initial conditons. τ = τ0, IC = 1 τ = τ0, IC = 2 τ = 4τ0, IC = 1 τ = 4τ0, IC = 2 τ0 corresponds to a delay of 12 minutes in the dimensional model A delay of τ0 induces a patterning lag of about 60τ0 A delay of 4τ0 induces a patterning lag of about 240τ0 x x
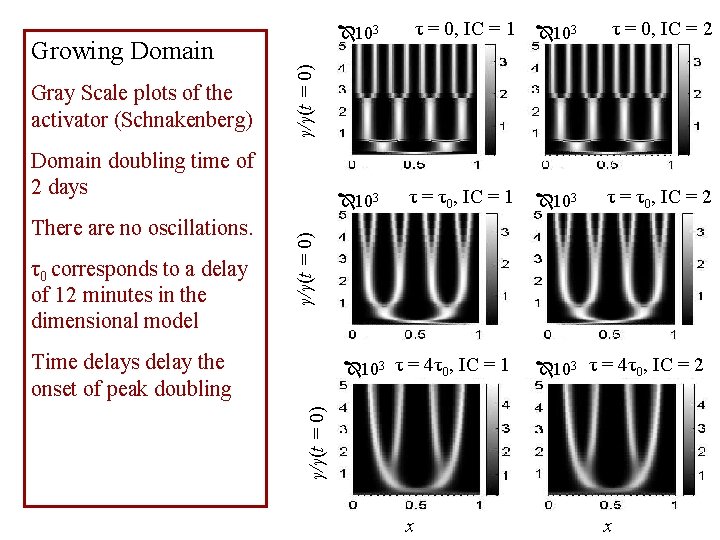
Gray Scale plots of the activator (Schnakenberg) Domain doubling time of 2 days τ0 corresponds to a delay of 12 minutes in the dimensional model 103 τ = τ0, IC = 1 τ = τ0, IC = 2 103 γ/γ(t = 0) There are no oscillations. τ = 0, IC = 2 γ/γ(t = 0) Growing Domain τ = 0, IC = 1 103 Time delays delay the onset of peak doubling 103 τ = 4τ0, IC = 2 γ/γ(t = 0) 103 τ = 4τ0, IC = 1 x x
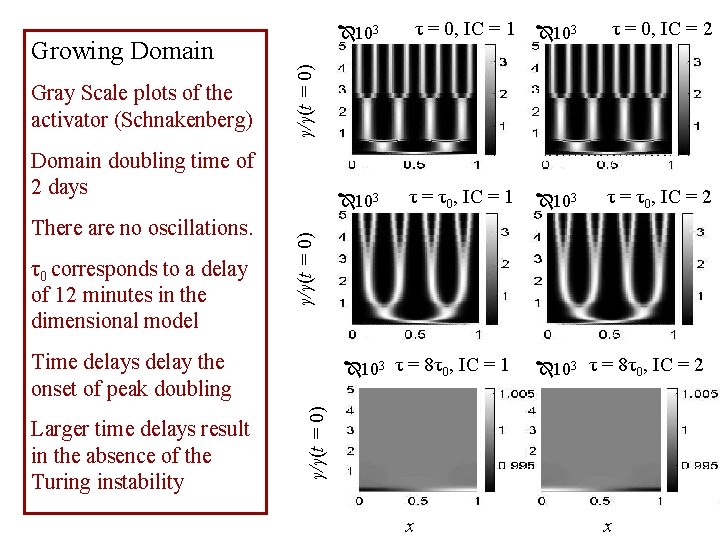
Gray Scale plots of the activator (Schnakenberg) Domain doubling time of 2 days τ0 corresponds to a delay of 12 minutes in the dimensional model 103 Time delays delay the onset of peak doubling τ = τ0, IC = 2 103 τ = 8τ0, IC = 1 103 τ = 8τ0, IC = 2 γ/γ(t = 0) Larger time delays result in the absence of the Turing instability τ = τ0, IC = 1 γ/γ(t = 0) There are no oscillations. τ = 0, IC = 2 γ/γ(t = 0) Growing Domain τ = 0, IC = 1 103 x x
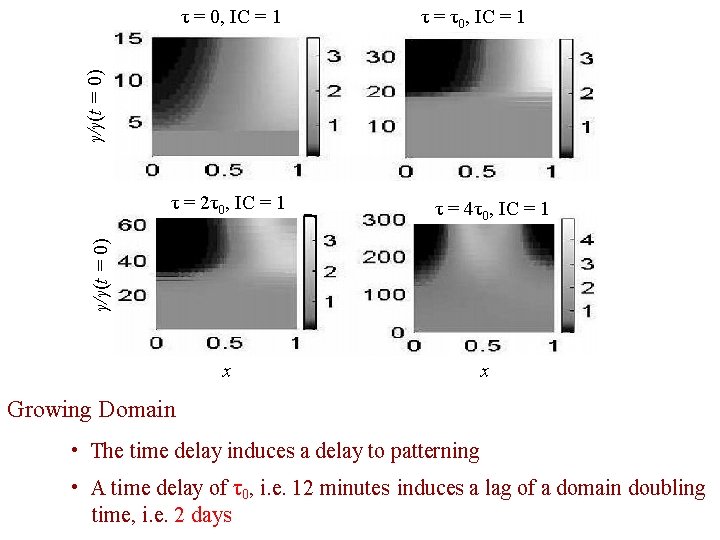
τ = τ0, IC = 1 γ/γ(t = 0) τ = 0, IC = 1 τ = 4τ0, IC = 1 γ/γ(t = 0) τ = 2τ0, IC = 1 x x Growing Domain • The time delay induces a delay to patterning • A time delay of τ0, i. e. 12 minutes induces a lag of a domain doubling time, i. e. 2 days

Domain Doubling Time: 2 days 103 τ = 4τ0, IC = 1 x τ ==τ10, IC = 2 τ 10 = 4τ330, IC 10 γ/γ(t = 0) 5 Domain Doubling Time: 12 hours τ = 4τ0, IC = 1 103 γ/γ(t = 0) 103 x Growing Domain • The behaviour of the system appears to be governed by the parameter grouping τδ = 2 ln(2) [Time Delay/Doubling Time]

Domain Doubling Time: 2 days 103 τ = 4τ0, IC = 1 τ ==τ10, IC = 2 τ 10 = 4τ330, IC 10 γ/γ(t = 0) 5 Domain Doubling Time: 12 hours τ = 4τ0, IC = 1 103 γ/γ(t = 0) 103 x x x Growing Domain • The behaviour of the system appears to be governed by the parameter grouping τδ = 2 ln(2) [Time Delay/Doubling Time]

τ = 4τ0, IC = 1 103 Domain Doubling Time: 2 days γ/γ(t = 0) x Growing Domain τ = 16τ0, IC = 1 τ ==16τ τ 10 = 4τ3 0, IC 1 0, IC = 2 γ/γ(t = 0) 103 Domain Doubling Time: 8 days τ = 4τ0, IC = 1 γ/γ(t = 0) 103 x x x • The behaviour of the system appears to be governed by the parameter grouping τδ = 2 ln(2) [Time Delay/Doubling Time]
x x
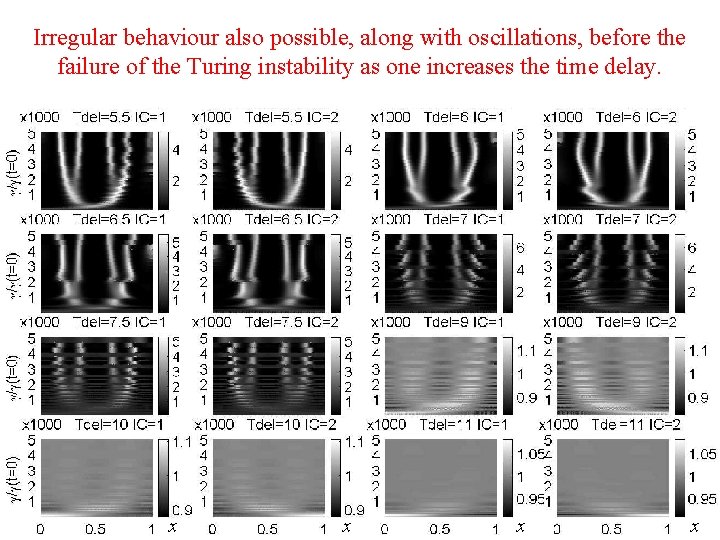
Irregular behaviour also possible, along with oscillations, before the failure of the Turing instability as one increases the time delay. x x

Schakenberg Model. Results. Summary Stationary Domain • No oscillations generally • Pattern is sensitive to the initial conditions • Time delays can induce a large patterning lag Growing Domain Results. Summary: • No oscillations generally • Time delays can induce a large patterning lag • Time delays can induce irregular behaviour and a failure of the Turing instability • The behaviour of the system is governed by the parameter grouping: τδ = 2 ln(2) [Time Delay/Doubling Time]

Conclusions. Time Delays and Biological RD Systems We have • motivated the biophysical need for the inclusion of signal transduction and gene expression time delays in models of biological pattern formation • We have demonstrated how these delays can be included in one of the simplest "long range activation-short range inhbition" pattern forming reaction diffusion models. While we have not typically found oscillations, we have found that • Time delays can make a large difference to the patterns emerging from the models, especially with regard to patterning lags and, for growing domains, the failure of the Turing instability Thus …

The above observations do not rule out reaction diffusion as a putative pattern formation mechanism, whether on a stationary or uniformly growing spatial domain. However, when considering patterning events especially those for which rapid establishment of pattern is critical, such as in the tissues of developing embryos, our results show that • any putative time delays cannot be neglected in general without careful justification. • our finding that time delays can dramatically increase the time taken for the reaction diffusion system to initiate patterns imposes potentially severe constraints on the potential molecular details of any Turing system that might operate during developmental patterning.

Future Work/Further Questions • Continue investigating the extent to which the results are general, especially for models with "short range activation, long range inhibition" – Kinetics with a negative feedback loop, e. g. Gierer Meinhardt – Kinetics with more than two componenents and multiple time delays. Are the patterning lags cumalative? – Other biological pattern formation mechanisms e. g. the mechanochemical models • If the results are general – We have, in general, potentially severe constraints on the reaction diffusion mechanism and other mechanisms of biological pattern formation • If the results are not general – there is a clear distinction between the patterning forming behaviour of "short range activation, long range inhibition" on the inclusion of time delays. This would have a substantial impact in that the choice of the kinetics really does matter!
Complicated extracellular domain. An exercise in homogeneisation theory:

The End






Caveats 2 Reaction Diffusion Patterns are observed to be very sensitive to • Perturbations of the domain shape. • Noise (in initial conditions and generally).

Background • In 1952 Turing proposed that – Pattern Formation during morphogenesis might arise through an instability in systems of reacting chemicals (morphogens), which is driven by diffusion. – Heterogenous concentrations of these chemicals form a “pre-pattern”. Subsequent differentiation of tissue/cell type is in response to whether or not one of these morphogens exceeds some threshold locally.

Typical Patterns Formed by This Mechanism Such a mechanism can often produce plausible looking results – Mammal coat patterns (Murray) And interesting, non-trivial, predictions – You shouldn’t be able to find a mammal with a striped body and a spotted tail.

Domain Growth Numerical Simulations of Kondo, Asai, Goodwin and others indicate that • domain growth can lead to robust pattern formation, ie. insensitivity to noise and randomness in the initial conditions. & motivates a detailed investigation of • the stabilising influence of domain growth • the mechanisms by which it produces robustness • conditions for which one may expect robust pattern formation

Arcuri & Murray Conclusions By observations of numerical simulations • domain growth yields a tendency towards robustness, but this is far from universal. This had led some theoretical biologists to dismiss Reaction Diffusion Even as a possible/plausible pattern formation mechanism (eg Saunders & Ho, Bull Math Bio, 1995). BUT • One should derive the Reaction Diffusion Equations with domain growth from conservation laws, not crude scaling arguments.

“Lock in” Thus we have frequency doubling cascades of self-similar patterns. Of course, one cannot expect to hold exactly in practice so a form of “start-near, stay near” stability is also required for a frequency doubling cascade.

Domain Growth: Initial Conclusions Incorporation of exponential domain growth initially appears to give • Robust pattern Formation, ie. No dependence on details of initial conditions • No need to fine tune the parameters • No need to fine tune the model.

Breakdown of Mode Doubling breaks for high and low growth rates. • Exponential Growth, Schnakenburg Kinetics

Breakdown of Mode Doubling Breakdown at High Growth rates appears to be due to the fact • Further peak reorganisation occurs before splitting peak reaches quasi-steady state. • This in turn prevents Lock in, ie a point where • As we get a total breakdown of pattern. For Low growth rates we also get breakdown …

Low Growth Rate Mode Doubling Breakdown Low Growth rate frequency doubling breakdown is • noise dependent • occurs after lock in •

General Conclusion Robust Pattern Formation occurs for exponential growth with Schnakenburg kinetics over 4 -5 orders of magnitude of the growth rate.

• Do not expect self similar cascade to proceed indefinitely for linear growth • Given Stability assumptions, if there is a such that or equivalently • then these coincide for Prediction: • If a sequence with a linear growth rate undergoes M frequency doublings before breakdown then – A sequence with a linear growth rate of M+1 frequency doublings. will undergo
- Slides: 63