RC RLC circuit and Magnetic field RC Charge

RC, RLC circuit and Magnetic field RC Charge relaxation RLC Oscillation Helmholtz coils

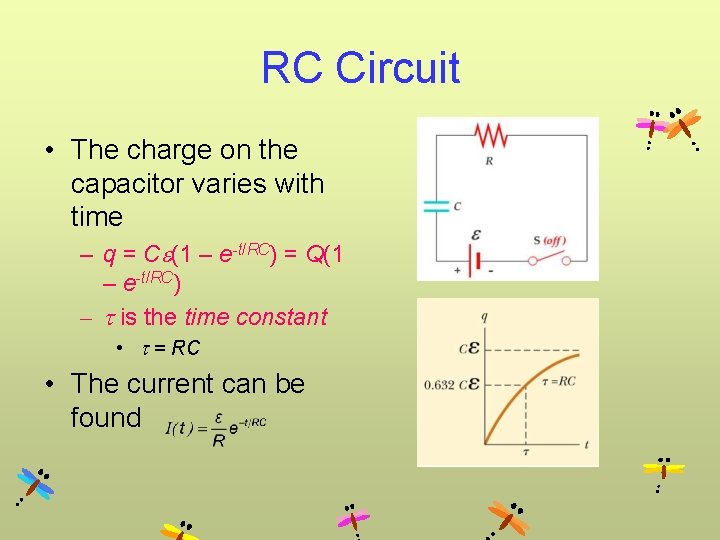
RC Circuit • The charge on the capacitor varies with time – q = Ce(1 – e-t/RC) = Q(1 – e-t/RC) – is the time constant • = RC • The current can be found

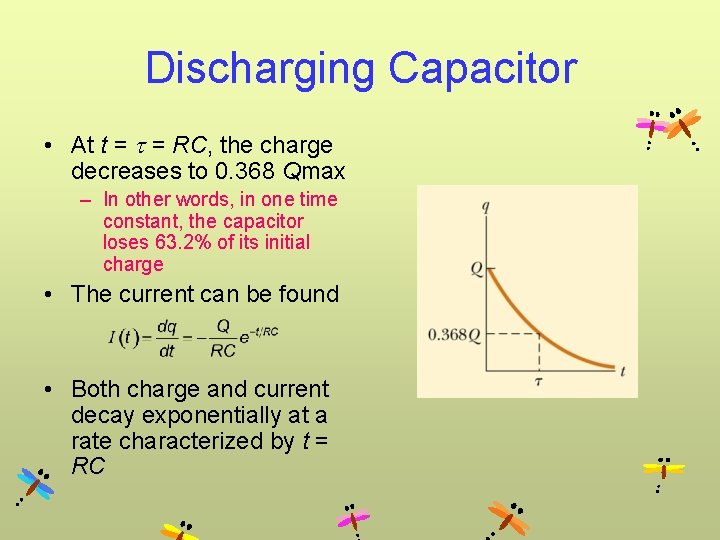
Discharging Capacitor • At t = = RC, the charge decreases to 0. 368 Qmax – In other words, in one time constant, the capacitor loses 63. 2% of its initial charge • The current can be found • Both charge and current decay exponentially at a rate characterized by t = RC

Oscillations in an LC Circuit • A capacitor is connected to an inductor in an LC circuit • Assume the capacitor is initially charged and then the switch is closed • Assume no resistance and no energy losses to radiation

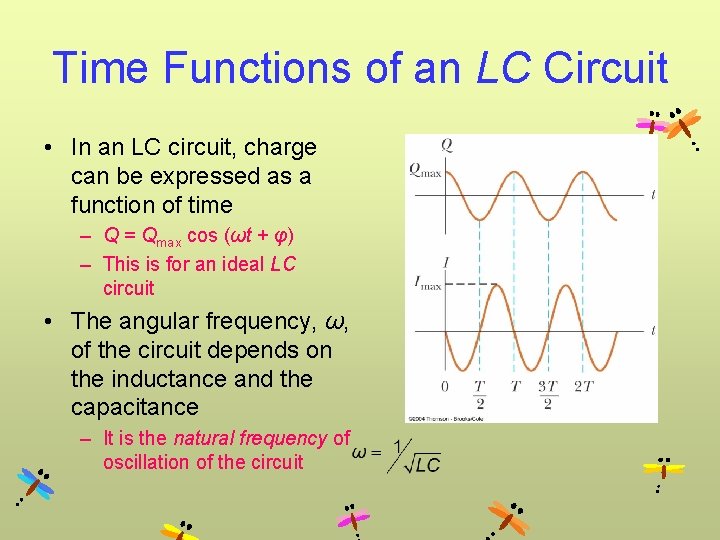
Time Functions of an LC Circuit • In an LC circuit, charge can be expressed as a function of time – Q = Qmax cos (ωt + φ) – This is for an ideal LC circuit • The angular frequency, ω, of the circuit depends on the inductance and the capacitance – It is the natural frequency of oscillation of the circuit

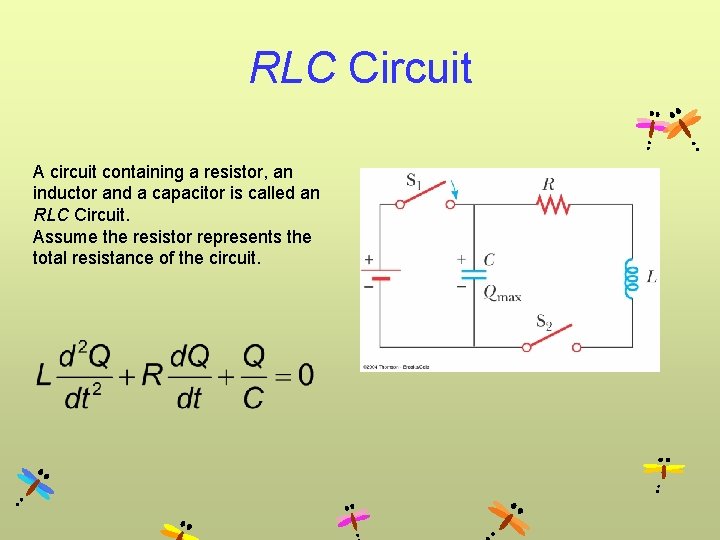
RLC Circuit A circuit containing a resistor, an inductor and a capacitor is called an RLC Circuit. Assume the resistor represents the total resistance of the circuit.

RLC Circuit Solution • When R is small: – The RLC circuit is analogous to light damping in a mechanical oscillator – Q = Qmax e-Rt/2 L cos ωdt – ωd is the angular frequency of oscillation for the circuit and

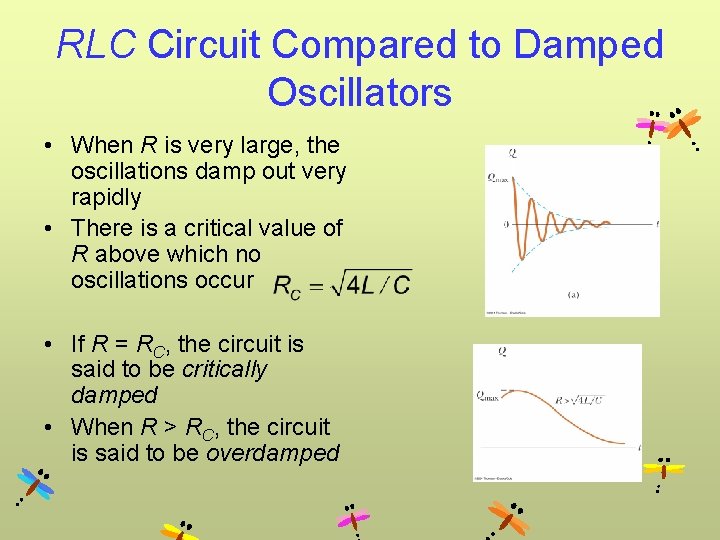
RLC Circuit Compared to Damped Oscillators • When R is very large, the oscillations damp out very rapidly • There is a critical value of R above which no oscillations occur • If R = RC, the circuit is said to be critically damped • When R > RC, the circuit is said to be overdamped

Biot-Savart Law • Biot and Savart conducted experiments on the force exerted by an electric current on a nearby magnet • They arrived at a mathematical expression that gives the magnetic field at some point in space due to a current

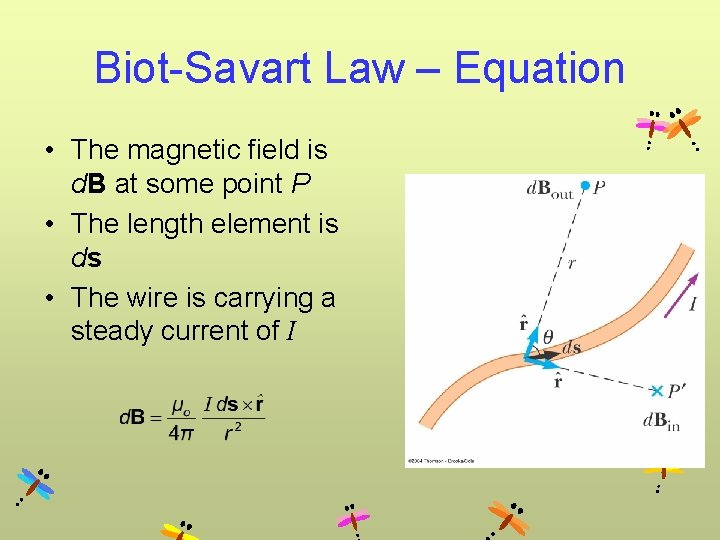
Biot-Savart Law – Equation • The magnetic field is d. B at some point P • The length element is ds • The wire is carrying a steady current of I

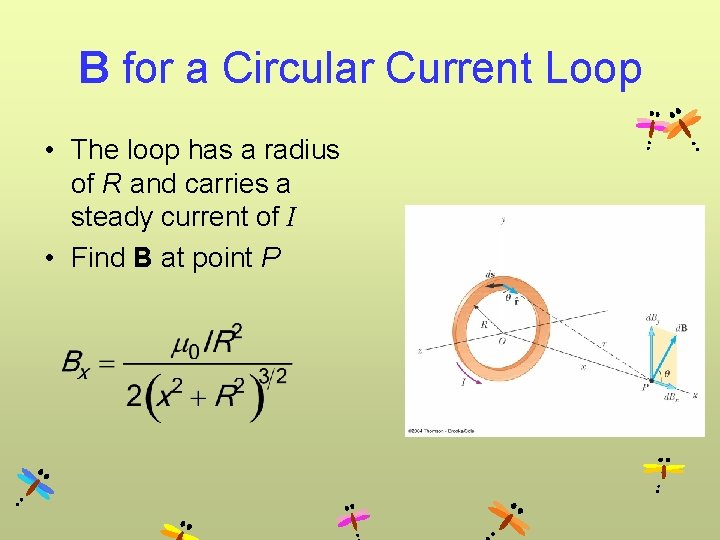
B for a Circular Current Loop • The loop has a radius of R and carries a steady current of I • Find B at point P

Helmholtz Coils (two N turns coils) If each coil has N turns, the field is just N times larger. At x=R/2 B is uniform in the region midway between the coils.