RAZLAGANJE GRAFOVA DFS algoritam Predstavljanje grafa matrica susedstva

RAZLAGANJE GRAFOVA DFS algoritam

Predstavljanje grafa – matrica susedstva •

Predstavljanje grafa – lista susedstva •

Matrica susedstva ili lista susedstva? •

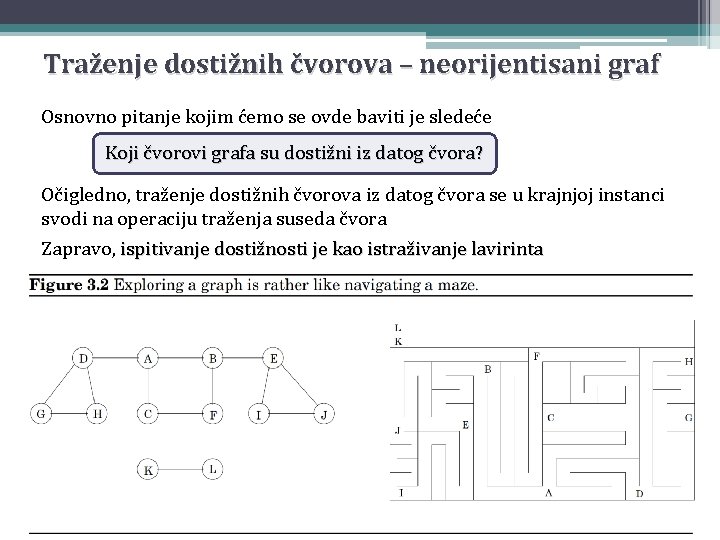
Traženje dostižnih čvorova – neorijentisani graf Osnovno pitanje kojim ćemo se ovde baviti je sledeće Koji čvorovi grafa su dostižni iz datog čvora? Očigledno, traženje dostižnih čvorova iz datog čvora se u krajnjoj instanci svodi na operaciju traženja suseda čvora Zapravo, ispitivanje dostižnosti je kao istraživanje lavirinta

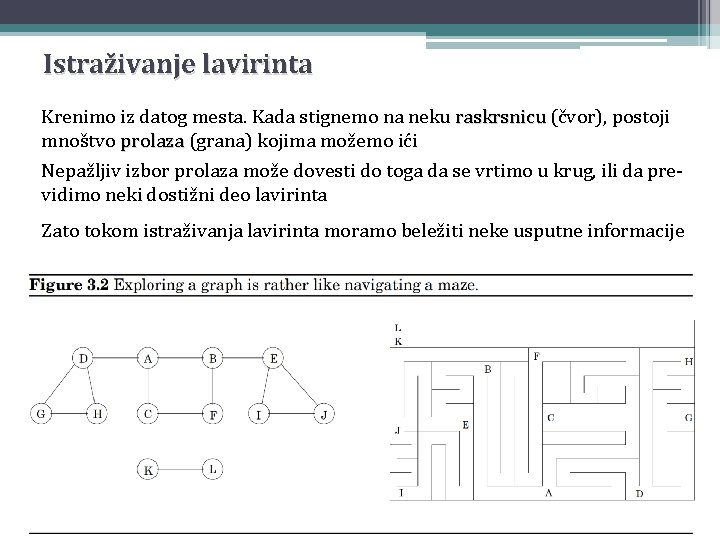
Istraživanje lavirinta Krenimo iz datog mesta. Kada stignemo na neku raskrsnicu (čvor), postoji mnoštvo prolaza (grana) kojima možemo ići Nepažljiv izbor prolaza može dovesti do toga da se vrtimo u krug, ili da previdimo neki dostižni deo lavirinta Zato tokom istraživanja lavirinta moramo beležiti neke usputne informacije

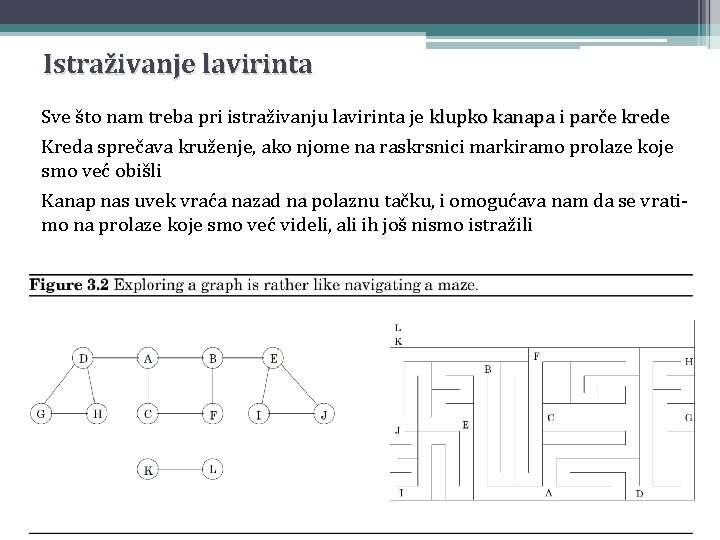
Istraživanje lavirinta Sve što nam treba pri istraživanju lavirinta je klupko kanapa i parče krede Kreda sprečava kruženje, ako njome na raskrsnici markiramo prolaze koje smo već obišli Kanap nas uvek vraća nazad na polaznu tačku, i omogućava nam da se vratimo na prolaze koje smo već videli, ali ih još nismo istražili

Istraživanje lavirinta Kako ćemo kredu i kanap simulirati na računaru? Ulogu krede može igrati Bulova promenljiva koju pridružujemo svakom čvoru i koja će nam ukazivati na to da li smo taj čvor već posetili Sa druge strane, ulogu kanapa može da igra stek Prava uloga kanapa je da omogući dve osnovne operacije ▫ odmotavanje, koje nas vodi do nove raskrsnice ▫ namotavanje, koje nas vraća na prethodnu raskrsnicu Kod steka, odmotavanje se ispoljava kao „uguravanje“ novog čvora (push), push a namotavanje kao „sklanjanje“ čvora sa vrha steka (pop) pop Ipak, mi ovde stek pominjemo tek iz metodoloških razloga, i nećemo ga koristiti eksplicitno, već samo implicitno, na način prikazan u sledećem algoritmu

Nalaženje dostižnih čvorova Uloga procedura previsit i postvisit je sledeća ▫ previsit nam kaže kada je čvor obiđen prvi put ▫ postvisit nam kaže kada je čvor obiđen poslednji put (i više se nećemo vraćati u njega)

Nalaženje dostižnih čvorova •

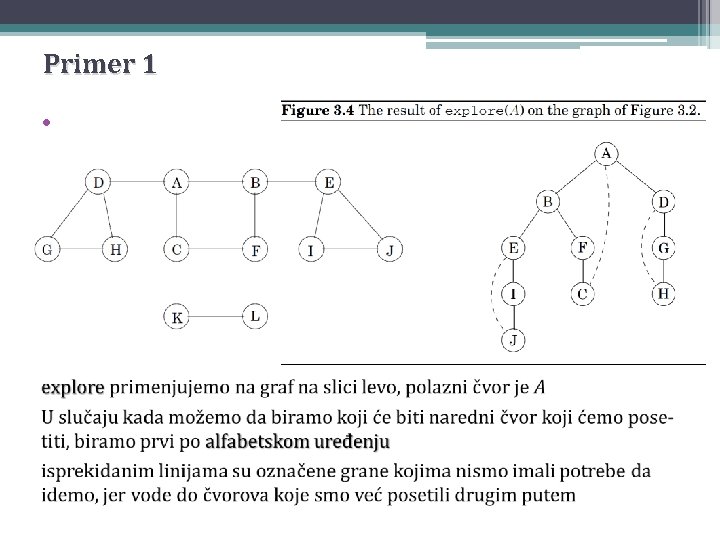
Primer 1 •

Pretraživanje po dubini – Dept-first search – DFS Procedura explore posećuje samo deo grafa koji je dostižan iz polaznog čvora procedure Da bi istražili ostatak grafa treba da restartujemo proceduru u bilo kom čvoru koji još uvek nije posećen, dok ne prođemo ceo graf To radi sledeći algoritam

Kompleksnost DFS •

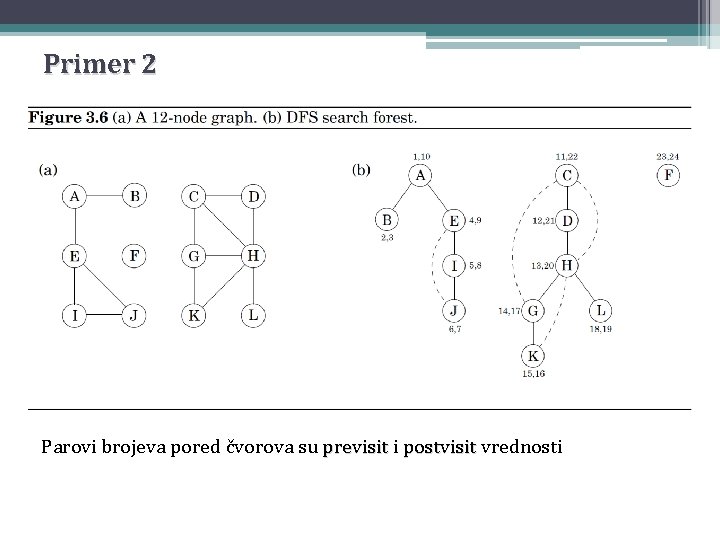
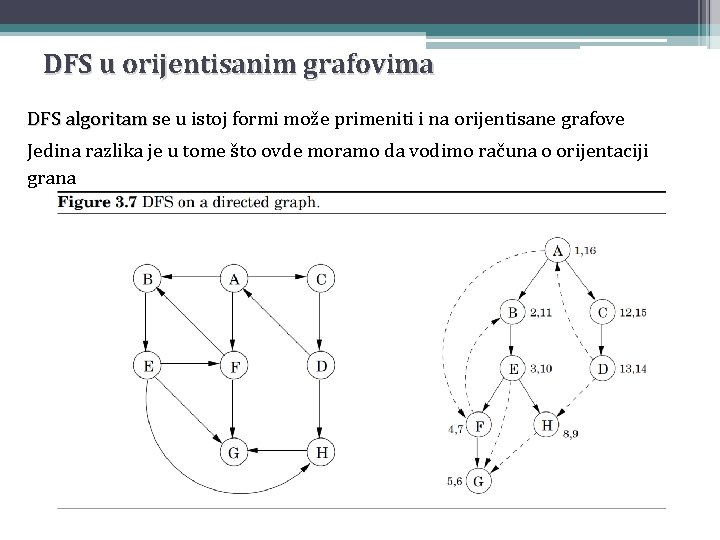
Primer 2 Parovi brojeva pored čvorova su previsit i postvisit vrednosti

Povezanost u neorijentisanim grafovima •

DFS u orijentisanim grafovima DFS algoritam se u istoj formi može primeniti i na orijentisane grafove Jedina razlika je u tome što ovde moramo da vodimo računa o orijentaciji grana

Tipovi grana Kod neorijentisanih grafova smo razlikovali dve vrste grana: „tree“ grane (grane u DFS stablu), i one koje to nisu (isprekidane linije) Kod orijentisanih grafova razlikujemo 4 tipa grana Odnosi predak-potomak, kao i tipovi grana, mogu se iščitati direktno iz pre i post brojeva

Tipovi grana •

Orijentisani aciklični grafovi To su orijentisani grafovi bez ciklusa (Directed acyclic graph – DAG) DAG izvor (source) – čvor kod koga nema ulaznih grana ponor (sink) – čvor kod koga nema izlaznih grana

Orijentisani aciklični grafovi Svojstvo 1: Orijentisani graf ima ciklus ako i samo ako DFS u njemu otkriva povratnu granu Svojstvo 2: U DAG-u, svaka grana vodi u čvor sa nižim post brojem Svojstvo 3: Svaki DAG ima bar jedan izvor (source) i bar jedan ponor (sink)

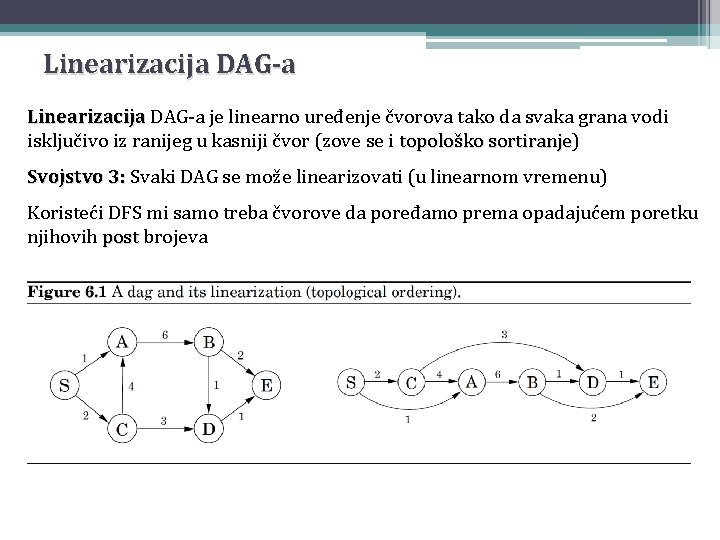
Linearizacija DAG-a je linearno uređenje čvorova tako da svaka grana vodi isključivo iz ranijeg u kasniji čvor (zove se i topološko sortiranje) sortiranje Svojstvo 3: Svaki DAG se može linearizovati (u linearnom vremenu) Koristeći DFS mi samo treba čvorove da poređamo prema opadajućem poretku njihovih post brojeva

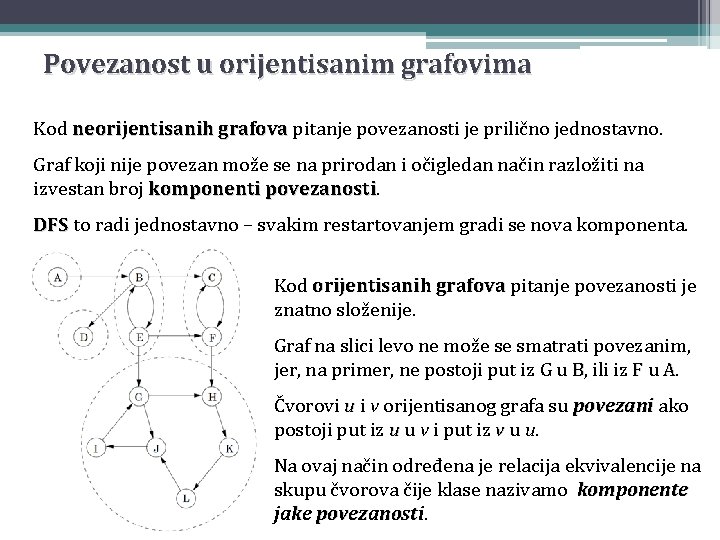
Povezanost u orijentisanim grafovima Kod neorijentisanih grafova pitanje povezanosti je prilično jednostavno. Graf koji nije povezan može se na prirodan i očigledan način razložiti na izvestan broj komponenti povezanosti DFS to radi jednostavno – svakim restartovanjem gradi se nova komponenta. Kod orijentisanih grafova pitanje povezanosti je znatno složenije. Graf na slici levo ne može se smatrati povezanim, jer, na primer, ne postoji put iz G u B, ili iz F u A. Čvorovi u i v orijentisanog grafa su povezani ako postoji put iz u u v i put iz v u u. Na ovaj način određena je relacija ekvivalencije na skupu čvorova čije klase nazivamo komponente jake povezanosti

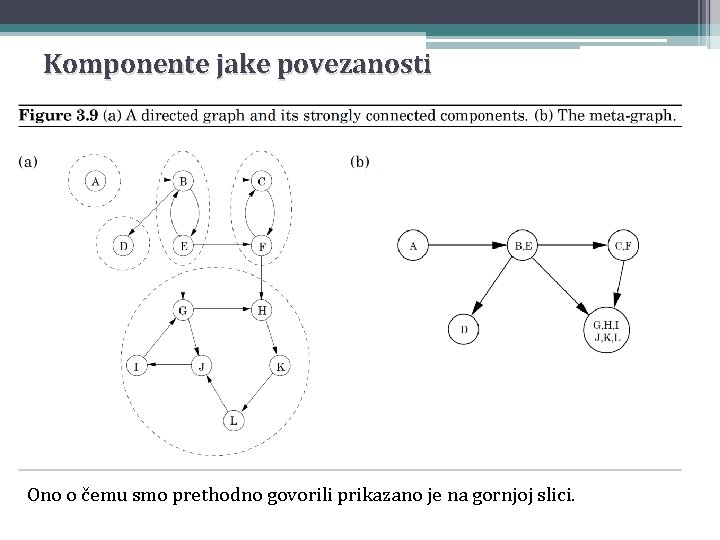
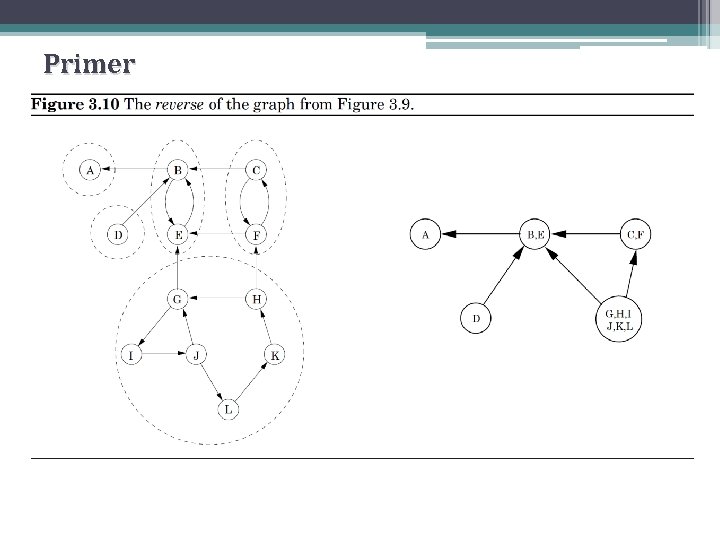
Komponente jake povezanosti Na slici levo komponente jake povezanosti su uokvirene isprekidanom linijom. Svaku od tih komponenti možemo sažeti u jedan čvor, takozvani meta-čvor, meta-čvor i možemo uzeti da postoji grana iz jednog meta-čvora u drugi ako postoji grana (isto orijentisana) između komponenti koje im odgovaraju Na taj način dobijamo meta-graf, meta-graf koji je DAG Naime, ako bi u meta-grafu postojao ciklus, onda bi on u originalnom grafu narušio različitost odgovarajućih komponenti jake povezanosti (sve te različite komponente bi spojio u jednu). Svojstvo: Svaki orijentisani graf je DAG svojih komponenti jake povezanosti

Komponente jake povezanosti Ono o čemu smo prethodno govorili prikazano je na gornjoj slici.

Efikasni algoritam Sada možemo dati efikasni algoritam za računanje komponenti jake povezanosti orijentisanog grafa, koji radi u linearnom vremenu i baziran je na DFS. Svojstvo 1: Ako se podprogram explore pokrene iz čvora u, on će se završiti tačno onda kada budu posećeni svi čvorovi dostižni iz u. u Dakle, ako pokrenemo explor e iz čvora koji leži u komponenti jake povezaexplore nosti koja je sink u meta-grafu, onda će explore dati upravo tu komponentu. Ovo otvara dva pitanja: (A) Kako pronaći čvor za koji ćemo biti sigurni da leži u komponenti jake povezanosti koja je sink u meta-grafu? (B) Kako da nastavimo dalje kada otkrijemo jednu komponentu? Ne postoji jednostavan način da pronađemo čvor koji leži u komponenti jake povezanosti koja je sink u meta-grafu, ali postoji način da se nađe čvor koji leži u komponenti koja je source u meta-grafu.

Efikasni algoritam Svojstvo 2: Čvor kome je dodeljen najveći post broj u DFS mora da leži u komponenti jake povezanosti koja je source u meta-grafu. Ovo je posledica opštijeg rezultata: Svojstvo 3: Ako su C i C’ komponente jake povezanosti, i ako postoji grana iz čvora iz C u čvor iz C’ , tada je najveći post broj u C veći od najvećeg post broja u C’. Dokaz: Ako je DFS komponentu C posetio pre komponente C’ , onda će obići sve čvorove iz C i C’ pre no što se zaglavi (Svojstvo 1). To znači da će prvi čvor iz C koga je DFS obišao imati veći post broj od svakog čvora iz C’. Sa druge strane, ako je DFS najpre posetio C’ , tada će se DFS zaglaviti nakon što obiđe sve čvorove iz C’ , a pre no što obiđe neki čvor iz C , pa opet zaključujemo da važi ono što se tvrdi u Svojstvu 3.

Efikasni algoritam

Efikasni algoritam

Primer