Ray tracing and ABCD matrix Optics Eugene Hecht

Ray tracing and ABCD matrix Optics, Eugene Hecht, Chpt. 6

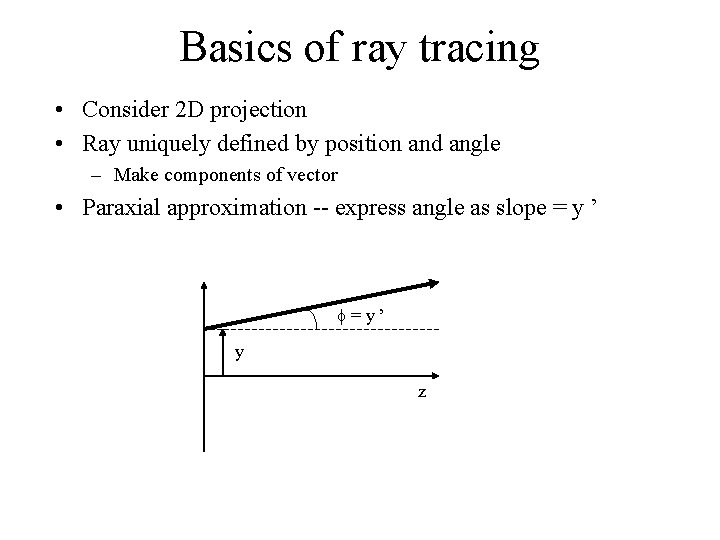
Basics of ray tracing • Consider 2 D projection • Ray uniquely defined by position and angle – Make components of vector • Paraxial approximation -- express angle as slope = y ’ f=y’ y z

Example: Propagate distance L • Angle (slope) unchanged • Position depends on initial position and slope (y 1, y 1’) (y 0, y 0’)

Example: Go through lens • Position unchanged • Angle (slope) change depends on position & focal length (y 0, y 0’) (y 1, y 1’)

ABCD matrix • Generalize • Can cascade to make single matrix for system • Example: go through lens and propagate distance L = f (y 0, y 0’) (y 1, y 1’) (y 2, y 2’)

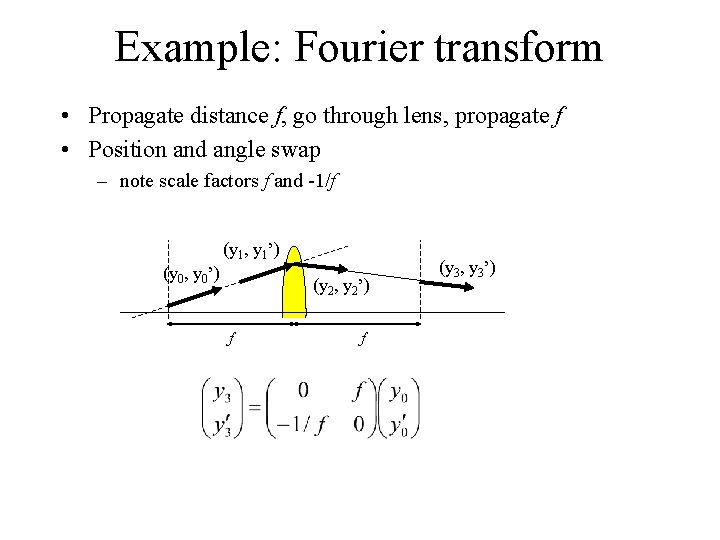
Example: Fourier transform • Propagate distance f, go through lens, propagate f • Position and angle swap – note scale factors f and -1/f (y 1, y 1’) (y 0, y 0’) (y 2, y 2’) f f (y 3, y 3’)

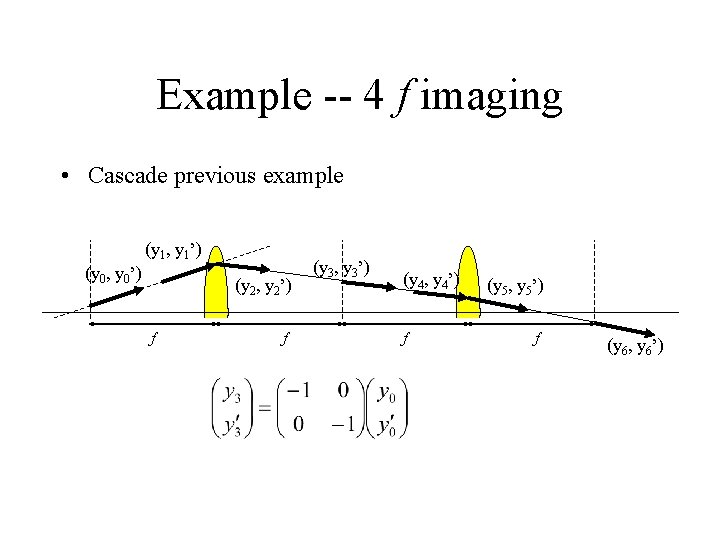
Example -- 4 f imaging • Cascade previous example (y 1, y 1’) (y 0, y 0’) (y 2, y 2’) f f (y 3, y 3’) (y 4, y 4’) f (y 5, y 5’) f (y 6, y 6’)

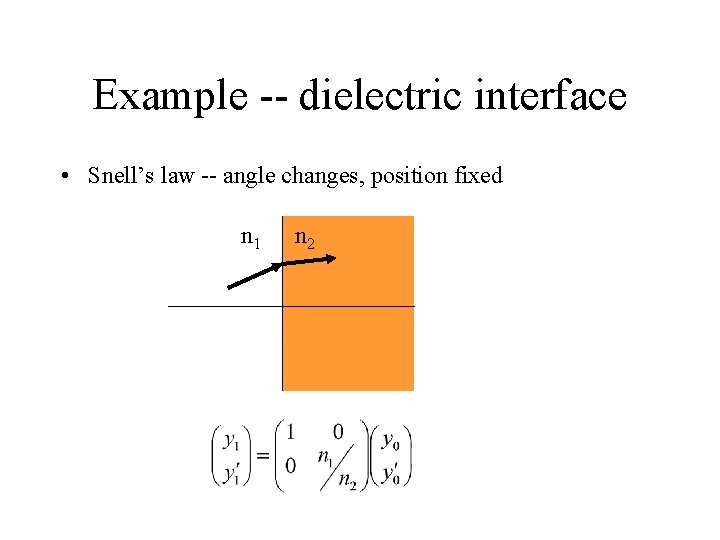
Example -- dielectric interface • Snell’s law -- angle changes, position fixed n 1 n 2

Other examples • Easy to generate ABCD matrices GRIN lens

Optical resonator • Condition for stable cavity • Return to initial state after integer N round trips