RATIOS AND STANDARDIZATION RATIOS Ratio the value obtained

RATIOS AND STANDARDIZATION

RATIOS Ratio - the value obtained when one quantity is divided by another: Proportion – a ratio where the numerator is part of the denominator # diseased/(# diseased + # not diseased) Percentage – proportion * 100 [# diseased/(# diseased + # not diseased)]*100 Example: Say we have 15 diseased people and 30 not diseased, then: proportion diseased: 15/(15+30) = 15/45 = 1/3 percentage diseased: 1/3 * 100 = 33. 3%

RATIOS Another common ratio: Rate - change in one quantity divided by change in another quantity (usually a measure of time) – – Incidence rate: number of new cases in an initially disease free population person-time Mortality rate: number of deaths in a population person-time

RATIOS Example: have 5 deaths in a population of 50 person months Mortality rate: 5/50 = 0. 10 or 0. 1 death person month Which is equivalent to 1 deaths per 10 person months or 10 deaths per 100 person months

RATIOS •

RATIOS •

RATIOS •

EXAMPLE FOR RATIOS -----------XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXD ---------------------------XXXXXXXXXXXXXXXXXXXXXXX ---------------------------------------------------------------------------------------------------------------D ------------------------------------------------------XXXXXXXD _______________________________________ JAN FEB MARCH APRIL MAY JUNE JULY AUGUST SEPT X = HAS DISEASE D = DIED --- = NO DISEASE PERSON-MONTHS = NUMBER OF MONTHS EACH PERSON WAS DISEASE FREE IN THE STUDY Find: proportion with disease? prevalance of disease? cumulative incidence? incidence rate until June

RATIOS OF RATIOS • Obese Not obese Total Below poverty 113 423 536 3. 5 times poverty 128 947 1075

RATIOS OR RATIOS What is the probability of a male child aged 2 -19 being obese if they reside in a poverty level family? What if they reside in a family whose income is 3. 5 times higher than the poverty level? What is the Relative Risk?

RATIOS OF RATIOS • Disease No Disease Total One copy gene variant 50 50 100 No copy gene variant 2 98 100

RATIOS OF RATIOS What are the odds of disease in the presence of the gene variant? What are the odds of disease in the absence of the gene variant? What is the Odds Ratio?
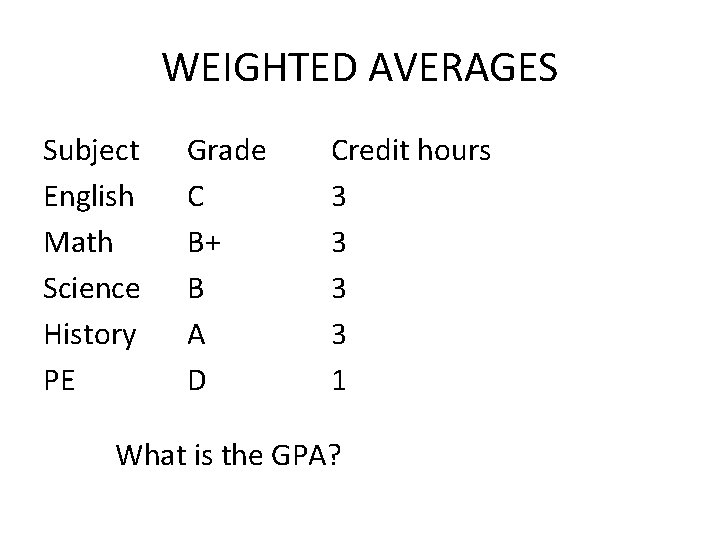
WEIGHTED AVERAGES Subject English Math Science History PE Grade C B+ B A D Credit hours 3 3 1 What is the GPA?

WEIGHTED AVERAGES GPA is a weighted average with the credit hours of each course as the weights GPA = Σ(numeric score*hours)/ Σ hours
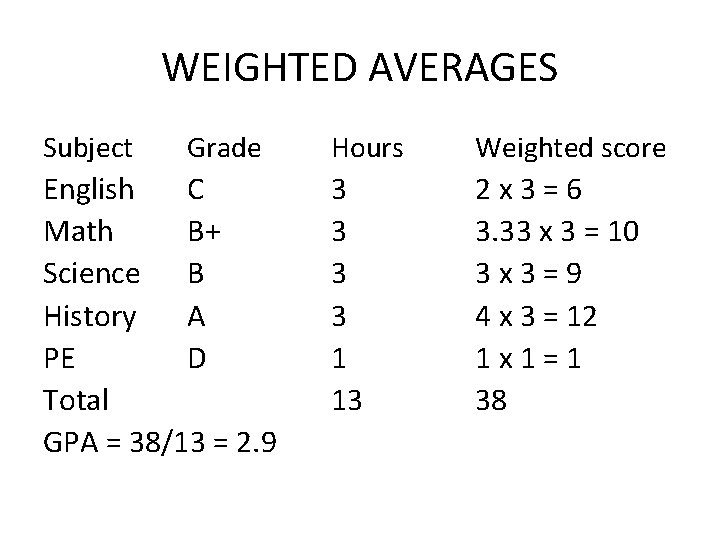
WEIGHTED AVERAGES Subject Grade English C Math B+ Science B History A PE D Total GPA = 38/13 = 2. 9 Hours Weighted score 3 3 1 13 2 x 3 = 6 3. 33 x 3 = 10 3 x 3 = 9 4 x 3 = 12 1 x 1 = 1 38

WEIGHTED AVERAGE An important and much used weighted average is the technique of STANDARDIZATION Study population(s) are compared using a ‘standard‘ population which is large and stable in size

STANDARDIZATION OF RATES Standardization refers to methods of adjustment based on weighted averages Two ways to control for an important characteristic (age, sex, race, etc) Direct Indirect

STANDARDIZATION OF RATES Direct method – uses the structure of a third ‘standard’ population and the rates of the populations to be compared – can compare two different populations Indirect method – uses the rates from a third ‘standard’ population and the structures of the populations to be compared – cannot compare two different population, can only compare each to a standard population used to calculate SMRs and SIRs

STANDARDIZATION OF RATES Example: have two populations: Group 1 has a crude mortality rate of 0. 017 per 1, 000 people per year Group 2 has a crude mortality rate of 0. 022 per 1, 000 people per year Group 1 crude mortality rate < Group 2 crude morality rate
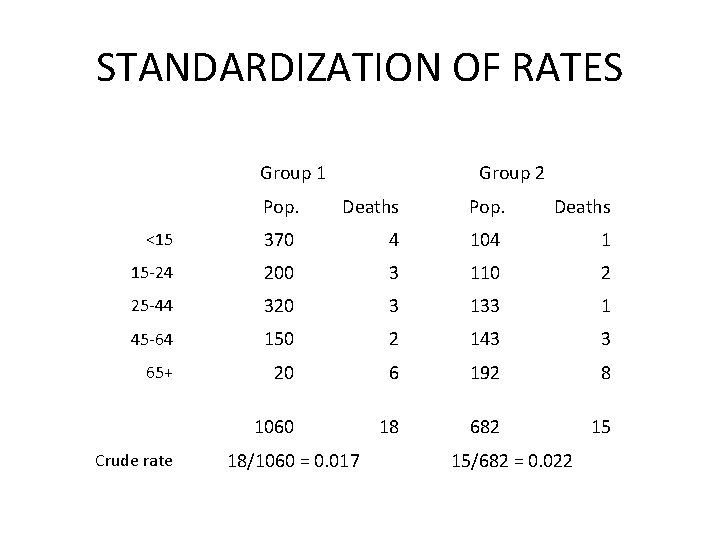
STANDARDIZATION OF RATES Group 1 Group 2 Pop. Deaths <15 370 4 104 1 15 -24 200 3 110 2 25 -44 320 3 133 1 45 -64 150 2 143 3 65+ 20 6 192 8 1060 18 682 15 Crude rate 18/1060 = 0. 017 15/682 = 0. 022

STANDARDIZATION OF RATES Choose a standard population (usually large and stable): Age groups Population Deaths <15 Rates 2, 400 20 0. 0083 15 -24 1, 900 17 0. 0089 25 -44 2, 100 14 0. 0067 45 -64 1, 900 21 0. 0111 65+ 1, 800 35 0. 0194 10, 100 107
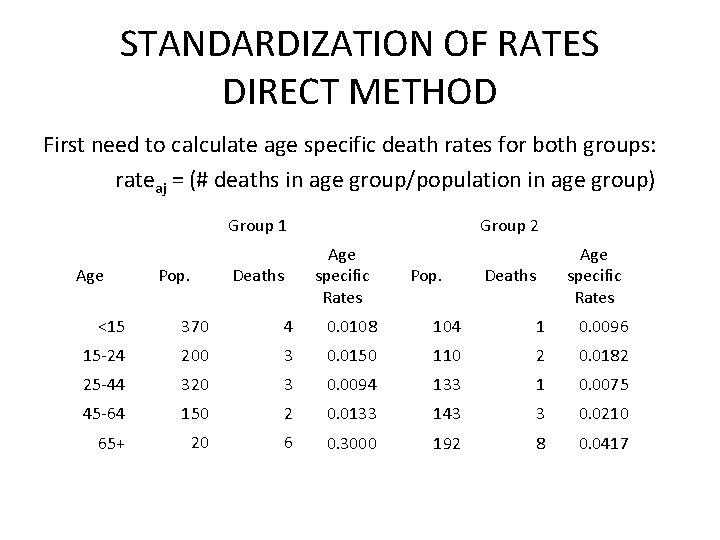
STANDARDIZATION OF RATES DIRECT METHOD First need to calculate age specific death rates for both groups: rateaj = (# deaths in age group/population in age group) Group 1 Age Pop. Group 2 Age specific Rates Deaths Pop. Age specific Rates Deaths <15 370 4 0. 0108 104 1 0. 0096 15 -24 200 3 0. 0150 110 2 0. 0182 25 -44 320 3 0. 0094 133 1 0. 0075 45 -64 150 2 0. 0133 143 3 0. 0210 65+ 20 6 0. 3000 192 8 0. 0417
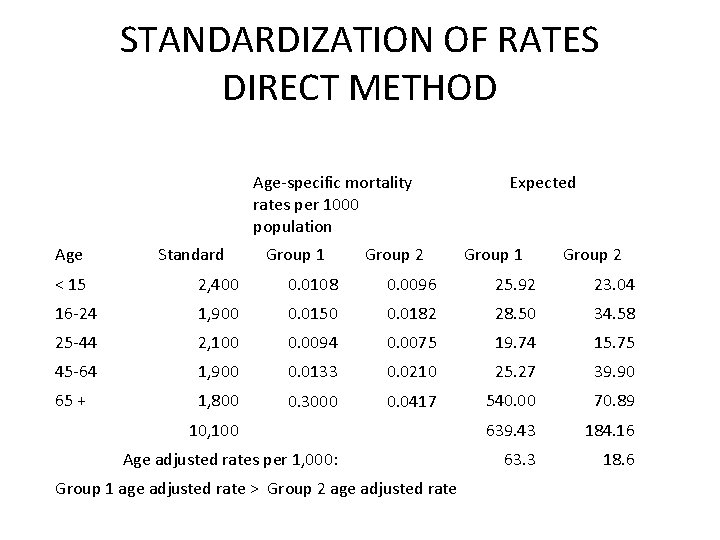
STANDARDIZATION OF RATES DIRECT METHOD Age-specific mortality rates per 1000 population Age Standard Group 1 Group 2 Expected Group 1 Group 2 < 15 2, 400 0. 0108 0. 0096 25. 92 23. 04 16 -24 1, 900 0. 0150 0. 0182 28. 50 34. 58 25 -44 2, 100 0. 0094 0. 0075 19. 74 15. 75 45 -64 1, 900 0. 0133 0. 0210 25. 27 39. 90 65 + 1, 800 0. 3000 0. 0417 540. 00 70. 89 639. 43 184. 16 63. 3 18. 6 10, 100 Age adjusted rates per 1, 000: Group 1 age adjusted rate > Group 2 age adjusted rate
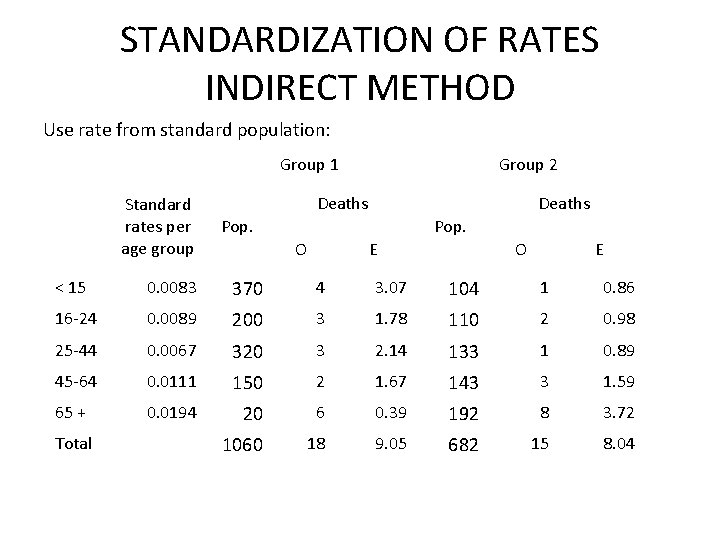
STANDARDIZATION OF RATES INDIRECT METHOD Use rate from standard population: Group 1 Standard rates per age group Group 2 Deaths Pop. O E < 15 0. 0083 370 4 3. 07 104 1 0. 86 16 -24 0. 0089 200 3 1. 78 110 2 0. 98 25 -44 0. 0067 320 3 2. 14 133 1 0. 89 45 -64 0. 0111 150 2 1. 67 143 3 1. 59 65 + 0. 0194 20 6 0. 39 192 8 3. 72 1060 18 9. 05 682 15 8. 04 Total

STANDARDIZATION OF RATES INDIRECT METHOD •
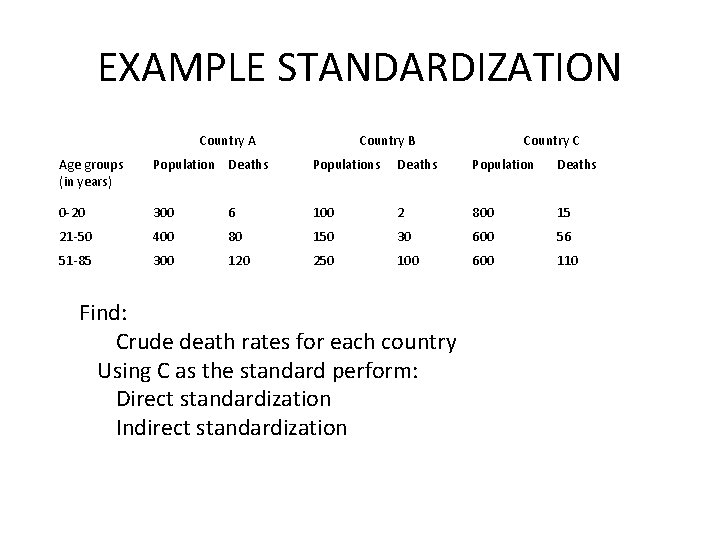
EXAMPLE STANDARDIZATION Country A Country B Country C Age groups (in years) Population Deaths Populations Deaths Population Deaths 0 -20 300 6 100 2 800 15 21 -50 400 80 150 30 600 56 51 -85 300 120 250 100 600 110 Find: Crude death rates for each country Using C as the standard perform: Direct standardization Indirect standardization
- Slides: 26