Ratios and Rates Chapter 7 Ratios A ratio




































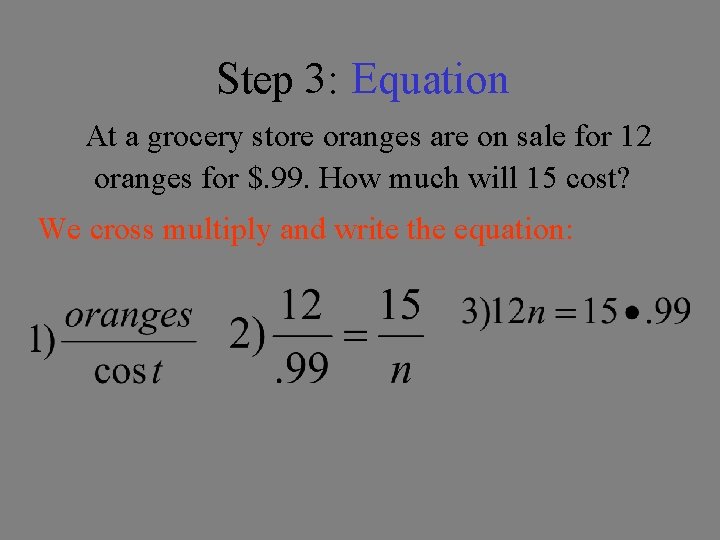
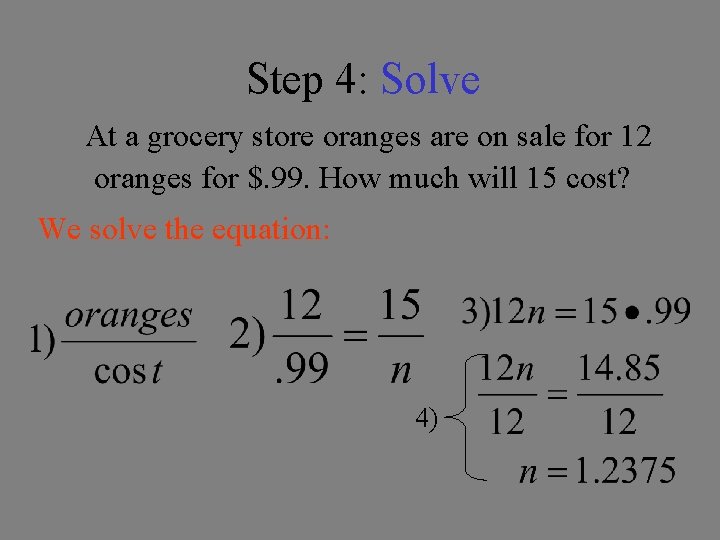
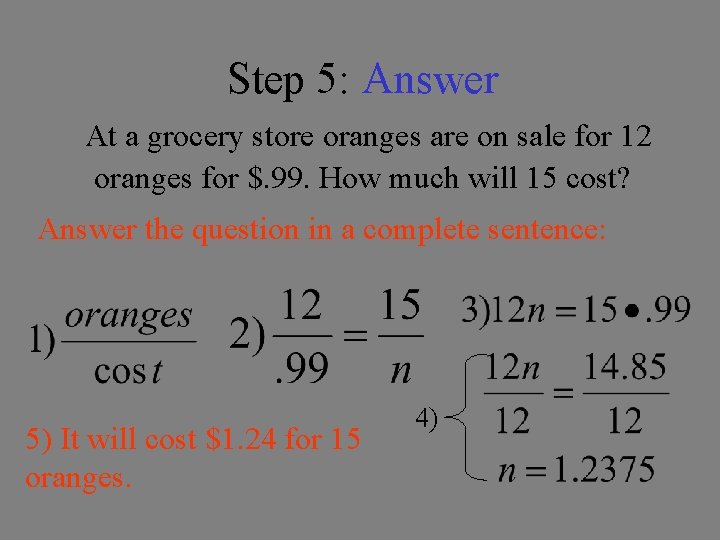

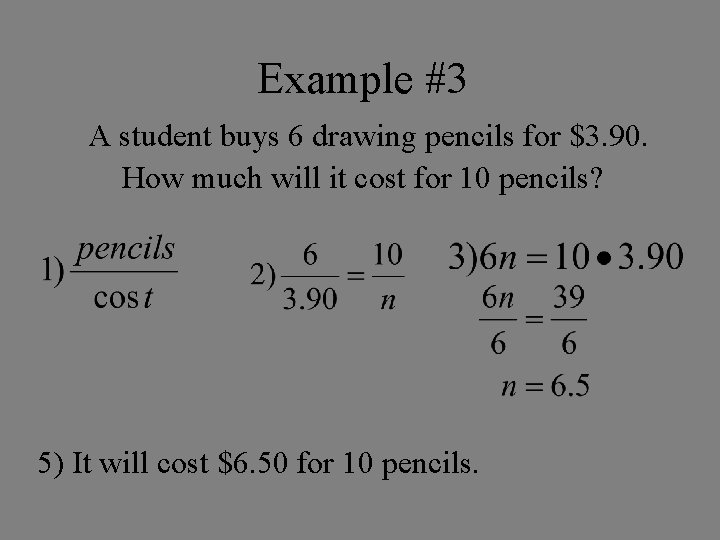

- Slides: 43

Ratios and Rates Chapter 7

Ratios • A ratio is a comparison of 2 things For example: What is the ratio of circles to squares? What is the ratio of squares to circles?

Ratios • We can write ratios in 3 ways: 1 to 2 1: 2 or ½ Always read as “ one to two” NEVER as “one half” because you are comparing one TO the other

Ratios What is the ratio of: • Phones to books? • Pencils to stars? • Stars to phones? • Pencils to books?

Ratios What is the ratio of: • Phones to books? 4 to 6 or 2 to 3 • Pencils to stars? • Stars to phones? • Pencils to books?

Ratios What is the ratio of: • Phones to books? 4 to 6 or 2 to 3 Pencils to stars? 2 to 4 or 1 to 2 • Stars to phones? • Pencils to books?

Ratios What is the ratio of: • Phones to books? 4 to 6 or 2 to 3 Pencils to stars? 2 to 4 or 1 to 2 • Stars to phones? 4 to 4 or 1 to 1 • Pencils to books?

Ratios What is the ratio of: • Phones to books? 4 to 6 or 2 to 3 Pencils to stars? 2 to 4 or 1 to 2 • Stars to phones? 4 to 4 or 1 to 1 • Pencils to books? 2 to 6 or 1 to 3

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks 2. 75 cents to 3 dollars 3. 2 pounds to 12 ounces

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks 2. 75 cents to 3 dollars 3. 2 pounds to 12 ounces They need to be in the same unit first

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks change weeks to days: 2. 75 cents to 3 dollars 3. 2 pounds to 12 ounces

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks change weeks to days: 2 days to 14 days 2. 75 cents to 3 dollars 3. 2 pounds to 12 ounces

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks change weeks to days: 2 days to 14 days or 1 to 7 2. 75 cents to 3 dollars 3. 2 pounds to 12 ounces

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks change weeks to days: 2 days to 14 days or 1 to 7 2. 75 cents to 3 dollars= 75¢ to 300 ¢ 3. 2 pounds to 12 ounces

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks change weeks to days: 2 days to 14 days or 1 to 7 2. 75 cents to 3 dollars= 75¢ to 300 ¢ or 1 to 4 3. 2 pounds to 12 ounces

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks change weeks to days: 2 days to 14 days or 1 to 7 2. 75 cents to 3 dollars= 75¢ to 300 ¢ or 1 to 4 3. 2 pounds to 12 ounces= 32 oz to 12 oz

Simplifying Ratios How can I simplify? 1. 2 days to 2 weeks change weeks to days: 2 days to 14 days or 1 to 7 2. 75 cents to 3 dollars= 75¢ to 300 ¢ or 1 to 4 3. 2 pounds to 12 ounces= 32 oz to 12 oz or 8 to 3

Simplifying Ratios Try these: 4. 2 days to 5 hours 5. 4 feet to 15 inches 6. 2 cm to 12 mm

Special Ratios Sometimes ratios can not be changed into the same unit For example: Simplify 420 miles to 15 gallons. We can not change miles to gallons or gallons to miles because one is measuring distance and the other is measuring capacity.

These special Ratios are called Rates A rate is a ratio expressed in a per unit form; that is, a form involving the ratio of some number to 1. It is therefore simplified to a whole number, a mixed number or a decimal by dividing. One example of a rate is "miles per gallon" (mpg, or mi/gal), which tells how far a car can travel on 1 gallon of gas. Can you think of any others?

Rates 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Examples of RATES: Words per minute: wpm Revolutions per minute: rpm Miles per gallon: mpg Miles per hour: mph Cost per week: $200 a week Cost per day: $50 a day Feet per second: ft/s Grams per cm 3 : g/ cm 3 Pounds per ft 3 : lb/ ft 3 Km per L: km/L

Rates Let's practice expressing rates in per unit form: 1) 522 words in 9 min = ? Words per min. 2) 125 miles in 2 hours 3) 16 g in 20 cm 3 4) 630 miles on 30 gal of gas

Rates Let's practice expressing rates in per unit form: 5) 120 km in 3 h 6) 70 mi on 5 gal of gas 7) $1000 in 4 months 8) A certain kind of lumber costs $3. 00 for 8 ft. What is the unit price (rate of cost)?

Rates We often associate rate with speed. The formula d=rt allows us to solve problems involving distance (d), average or constant rate of speed (r), and time (t). Let's try these: 1) A car made a trip of 225 mi at an average speed of 50 mi/h. How long did the trip take? (d = rt)

Rates Let's try these: 2) A car travels for 3 h at an average rate of speed of 65 km/h. How far does the car travel? 3) A bicyclist travels for 2 h at an average speed of 12 km/h. How far does the bicyclist travel?

Rates Let's try these: 4) At this speed(number 3), how long will it take the bicyclist to travel 54 km? 5) If a car travels 195 km in 3 h, what is its average rate of travel?

Proportions

Proportions • A proportion is 2 ratios that are equivalent For example: What is the ratio of circles to squares? 4: 6 or 2: 3 Therefore 4: 6 = 2: 3 which makes a proportion

Proportions • We can write proportions in 3 ways: 1 to 2= 2 to 4 1: 2=2: 4 or Always read as: “ one is to two as two is to four” NEVER as “one half equals two-fourths” because you are comparing one TO the other

Proportions • Remember that we can cross multiply to check to make sure that it is a proportion

Solving Proportions • we can also cross multiply to find the missing number in a proportion • then solve the equation 3 n = 60

Try these: PS: They don’t always work out to a whole number

Proportions and Word problems

Solving proportional word problems There are five steps that I want you to use when solving proportional word problems: 1. Ratio in words 2. Write the proportion 3. Cross multiply/equation 4. Solve the equation 5. Answer in a sentence

Word problems with proportions Example #1 At a grocery store oranges are on sale for 12 oranges for $. 99. How much will 15 cost?

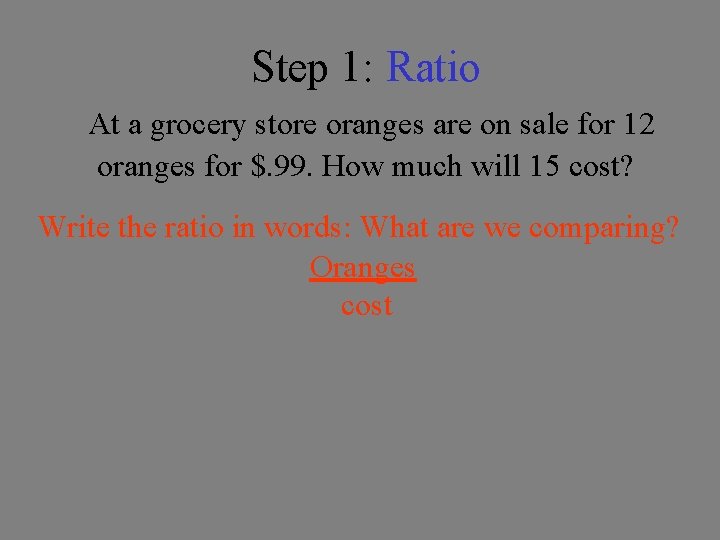
Step 1: Ratio At a grocery store oranges are on sale for 12 oranges for $. 99. How much will 15 cost? Write the ratio in words: What are we comparing? Oranges cost

Step 2: Proportion At a grocery store oranges are on sale for 12 oranges for $. 99. How much will 15 cost? Write the proportion with what we know: (We are comparing oranges to cost)
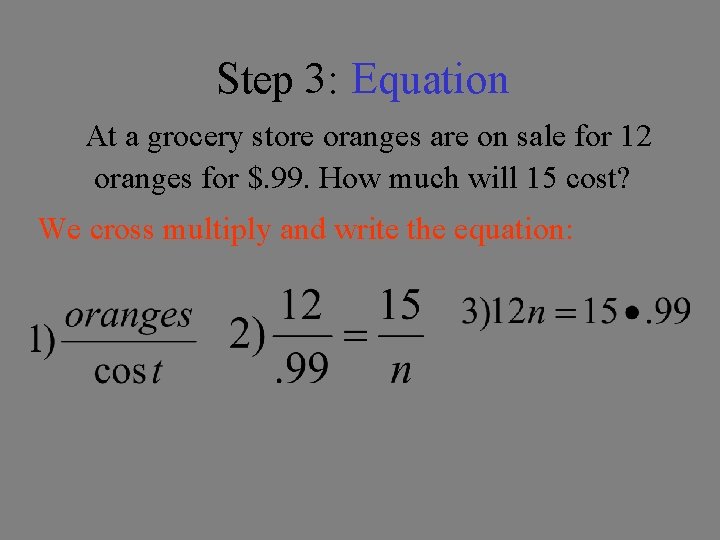
Step 3: Equation At a grocery store oranges are on sale for 12 oranges for $. 99. How much will 15 cost? We cross multiply and write the equation:
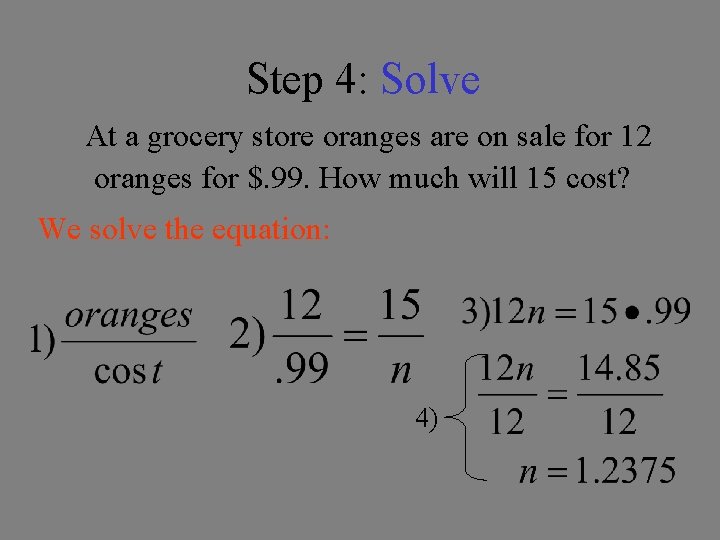
Step 4: Solve At a grocery store oranges are on sale for 12 oranges for $. 99. How much will 15 cost? We solve the equation: 4)
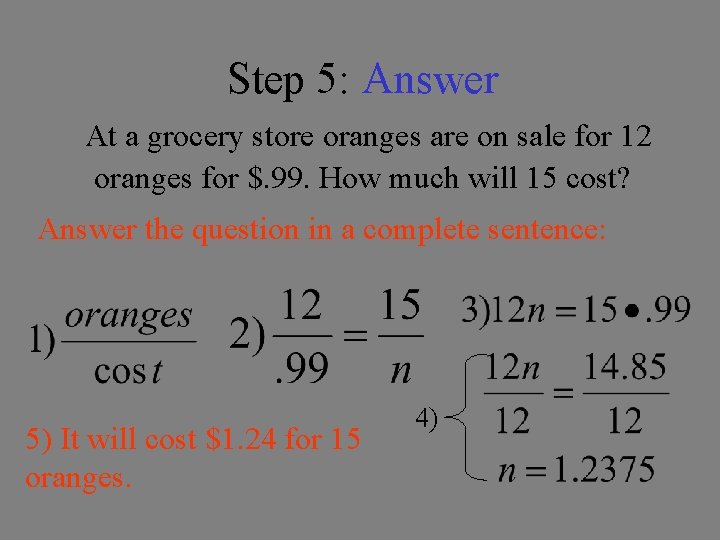
Step 5: Answer At a grocery store oranges are on sale for 12 oranges for $. 99. How much will 15 cost? Answer the question in a complete sentence: 5) It will cost $1. 24 for 15 oranges. 4)

Example #2 If 9 kg of fertilizer will feed 300 m 2 of grass, how much fertilizer will be required to feed 500 m 2? 5) 15 kg of fertilizer is required to feed 500 m 2
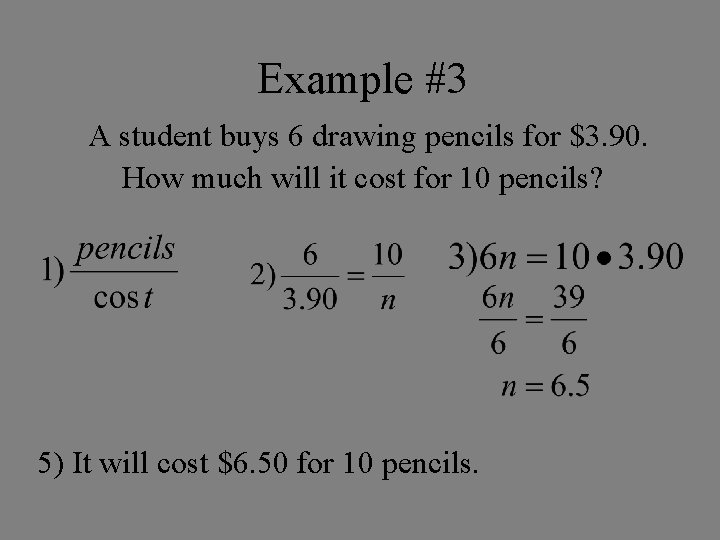
Example #3 A student buys 6 drawing pencils for $3. 90. How much will it cost for 10 pencils? 5) It will cost $6. 50 for 10 pencils.

Example #4 There are 221 students and 13 teachers at Hampton School. To keep the same student-toteacher ratio, how many teachers are needed for 272 students? 5) 16 teachers will be needed for 272 students.