Rational Functions and Models Lesson 4 5 Definition

Rational Functions and Models Lesson 4. 5

Definition l Consider a function which is the quotient of two polynomials Both polynomials l Example:

Long Run Behavior l Given l The long run (end) behavior is determined by the quotient of the leading terms l l Leading term dominates for large values of x for polynomial Leading terms dominate for the quotient for extreme x

Example l Given l Graph on calculator l Set window for -100 < x < 100, -5 < y < 5

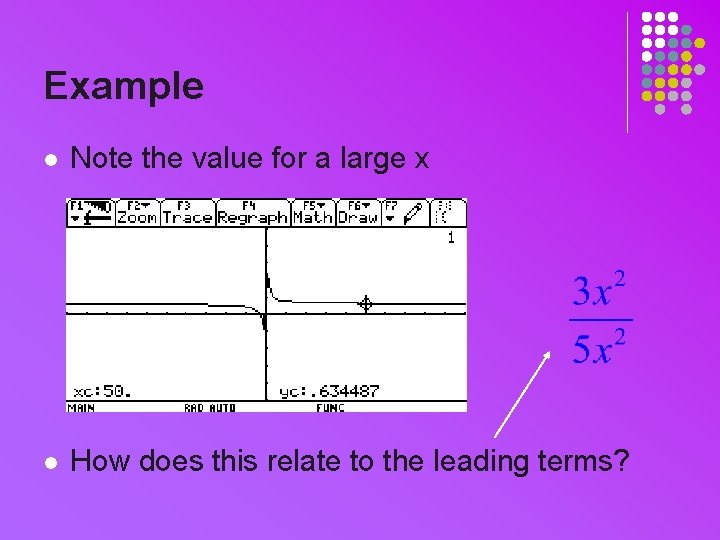
Example l Note the value for a large x l How does this relate to the leading terms?

Try This One l Consider l Which terms dominate as x gets large l What happens to l Note: l l as x gets large? Degree of denominator > degree numerator Previous example they were equal

When Numerator Has Larger Degree l Try l As x gets large, r(x) also gets large l But it is asymptotic to the line

Summarize Given a rational function with leading terms l When m = n l l When m > n l l Horizontal asymptote at 0 When n – m = 1 l Diagonal asymptote

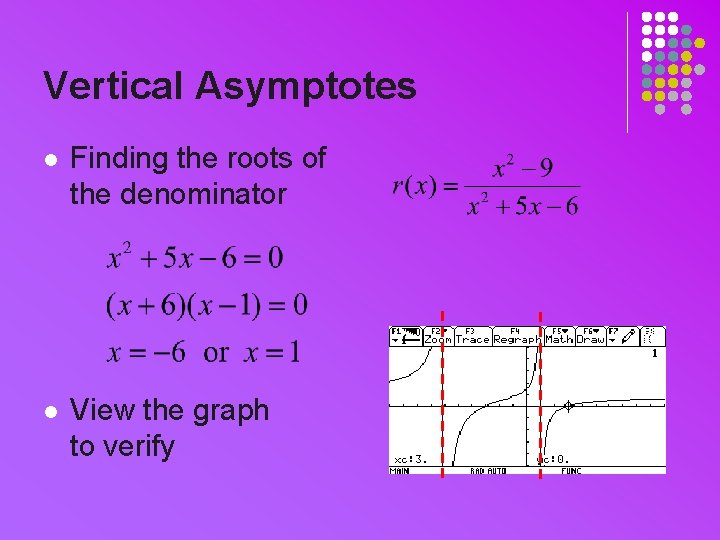
Vertical Asymptotes l A vertical asymptote happens when the function R(x) is not defined l This happens when the denominator is zero l Thus we look for the roots of the denominator l Where does this happen for r(x)?

Vertical Asymptotes l Finding the roots of the denominator l View the graph to verify

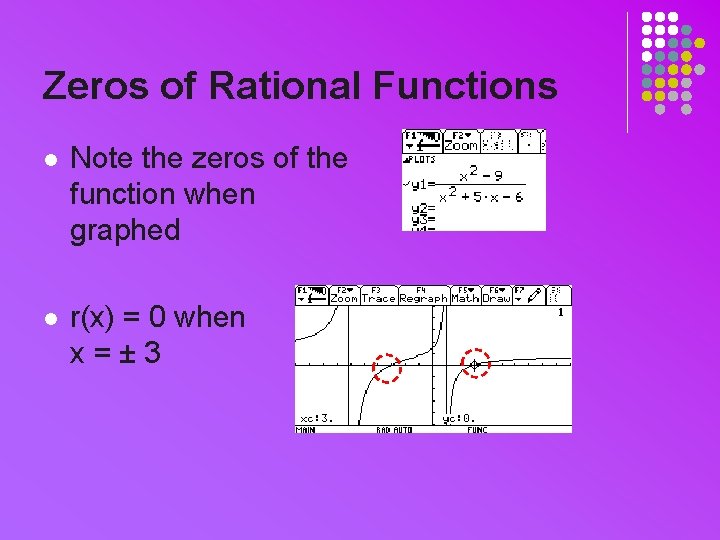
Zeros of Rational Functions l We know that l So we look for the zeros of P(x), the numerator l Consider l l What are the roots of the numerator? Graph the function to double check

Zeros of Rational Functions l Note the zeros of the function when graphed l r(x) = 0 when x=± 3

Summary l l The zeros of r(x) are where the numerator has zeros The vertical asymptotes of r(x) are where the denominator has zeros

Assignment l l l Lesson 4. 5 A Page 297 Exercises 1 – 61 Odd

Direct Variation l The variable y is directly proportional to x when: y=k*x This is a power • (k is some constant value) function l Alternatively l As x gets larger, y must also get larger • keeps the resulting k the same

Direct Variation l Example: l l l The harder you hit the baseball The farther it travels Distance hit is directly proportional to the force of the hit

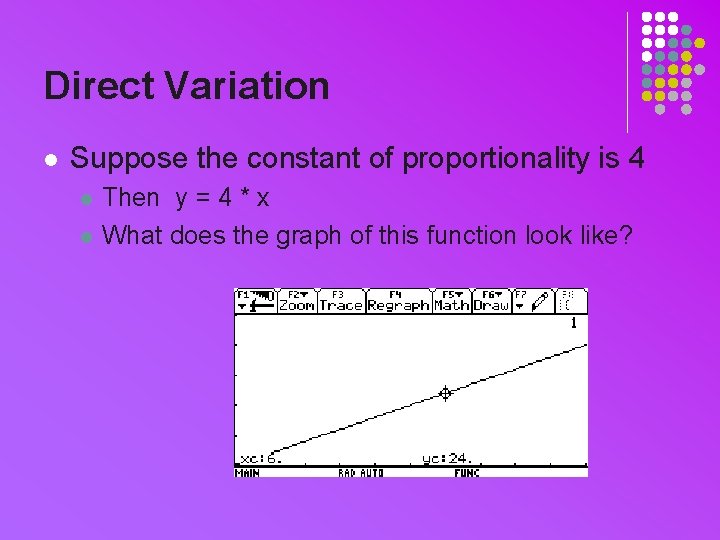
Direct Variation l Suppose the constant of proportionality is 4 l l Then y = 4 * x What does the graph of this function look like?

Inverse Variation l l l The variable y is inversely proportional to x when Alternatively y = k * x -1 As x gets larger, y must get smaller to keep the resulting k the same

Inverse Variation l Example: If you bake cookies at a higher temperature, they take less time l Time is inversely proportional to temperature

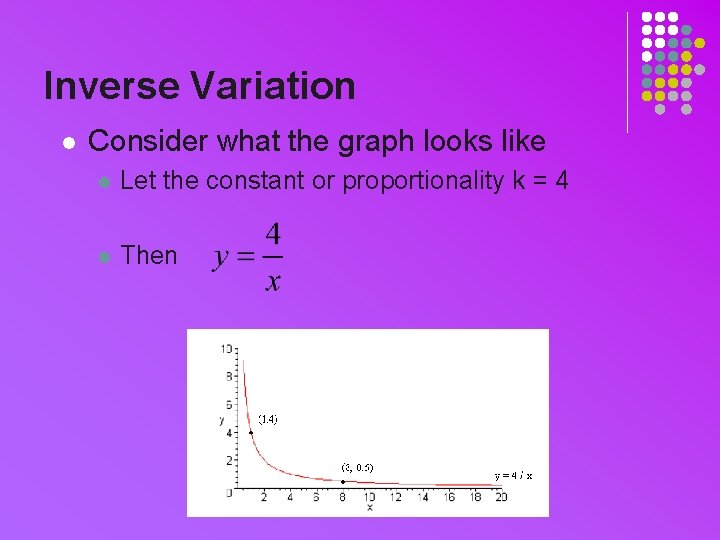
Inverse Variation l Consider what the graph looks like l Let the constant or proportionality k = 4 l Then

Assignment l l l Lesson 4. 5 B Page 299 Exercises 63 – 91 odd