Rational Functions and Models Identify a rational function




























- Slides: 34

Rational Functions and Models • Identify a rational function and state its domain • Identify asymptotes • Interpret asymptotes • Graph a rational function by using transformations • Graph a rational function by hand Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Rational Function (1 of 2) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Rational Function (2 of 2) The domain of a rational function includes all real numbers except the zeros of the denominator q(x). The graph of a rational function is continuous except at x-values where q(x) = 0. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Identifying rational functions (1 of 4) Determine if the function is rational and state its domain. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Identifying rational functions (2 of 4) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Identifying rational functions (3 of 4) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Identifying rational functions (4 of 4) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Vertical Asymptotes Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Horizontal Asymptotes (1 of 2) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Horizontal Asymptotes (2 of 2) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Finding Vertical & Horizontal Asymptotes (1 of 2) Vertical Asymptote To find a vertical asymptote, set the denominator, q(x), equal to 0 and solve. If k is a zero of q(x), then x = k is a vertical asymptote. Caution: If k is a zero of both q(x) and p(x), then f(x) is not written in lowest terms, and x − k is a common factor. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Finding Vertical & Horizontal Asymptotes (2 of 2) Horizontal Asymptote a. If the degree of the numerator is less than the degree of the denominator, then y = 0 (the x-axis) is a horizontal asymptote. c. If the degree of the numerator is greater than the degree of the denominator, then there are no horizontal asymptotes. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Finding asymptotes (1 of 5) For each rational function, determine any horizontal or vertical asymptotes. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Finding asymptotes (2 of 5) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Finding asymptotes (3 of 5) Degree of numerator is one less than the degree of the denominator so the x-axis, or y = 0, is a horizontal asymptote. When x = ± 2, the denominator, x² − 4, equals 0 and the numerator, x + 1 does not equal 0, so the vertical asymptotes are x = − 2 and x = 2. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Finding asymptotes (4 of 5) Degree of numerator is greater than the degree of the denominator so there are no horizontal asymptotes. When x = − 1, both the numerator and denominator equal 0 so the expression is not in lowest terms: There are no vertical asymptotes. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Finding asymptotes (5 of 5) The graph of h(x); a straight line with the point (− 1, − 2) missing. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Slant, or Oblique, Asymptotes (1 of 2) A third type of asymptote, which is neither vertical nor horizontal, occurs when the degree of the numerator of a rational function has degree one more than the degree of the denominator. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Slant, or Oblique, Asymptotes (2 of 2) The line y = x + 1 is a slant asymptote, or oblique asymptote of the graph of f. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Graphs and Transformations of Rational Functions Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

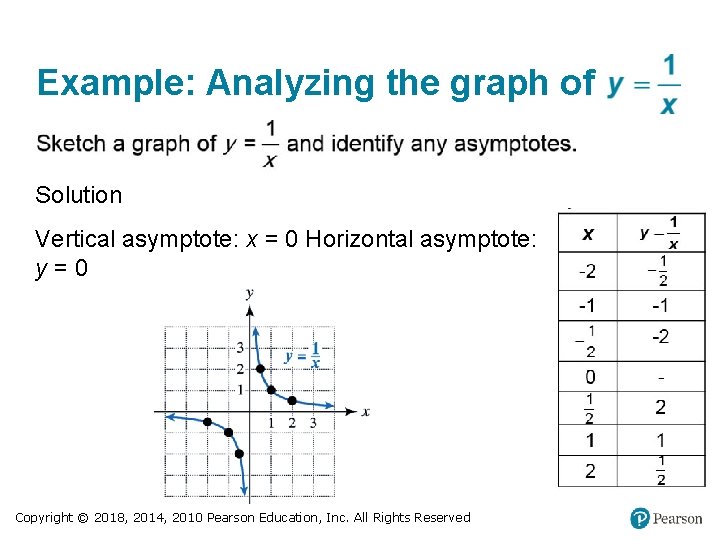
Example: Analyzing the graph of Solution Vertical asymptote: x = 0 Horizontal asymptote: y=0 Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

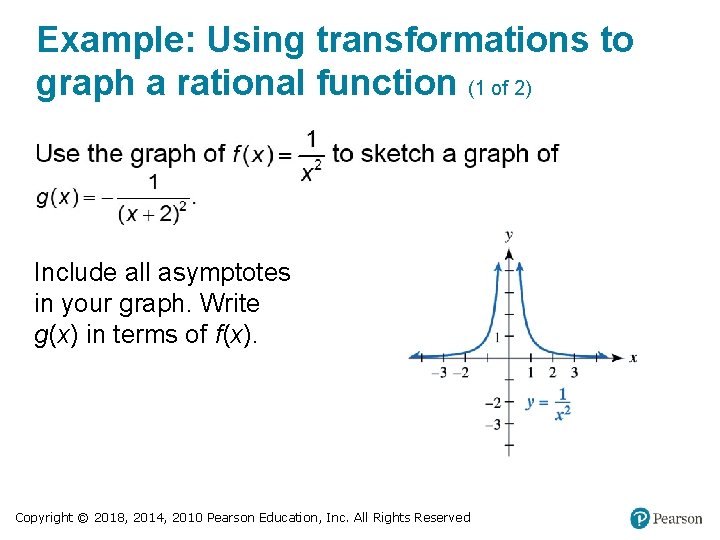
Example: Using transformations to graph a rational function (1 of 2) Include all asymptotes in your graph. Write g(x) in terms of f(x). Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

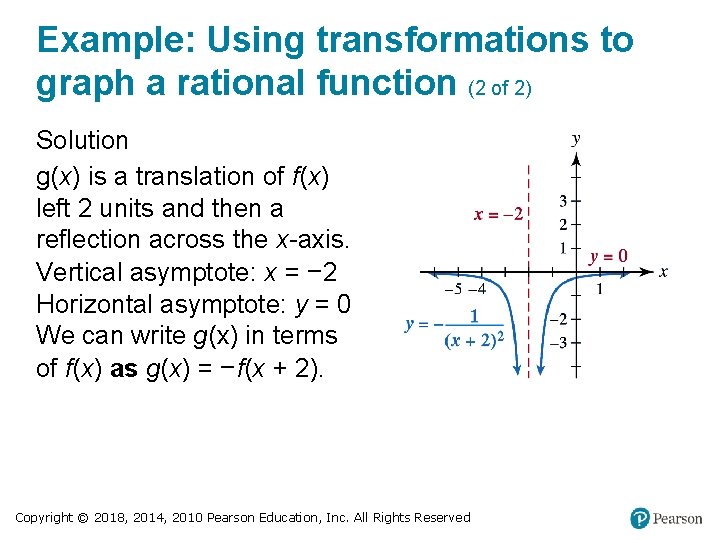
Example: Using transformations to graph a rational function (2 of 2) Solution g(x) is a translation of f(x) left 2 units and then a reflection across the x-axis. Vertical asymptote: x = − 2 Horizontal asymptote: y = 0 We can write g(x) in terms of f(x) as g(x) = −f(x + 2). Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Analyzing a rational function with technology (1 of 4) a. Use a calculator to graph f. Find the domain of f. b. Identify any vertical or horizontal asymptotes. c. Sketch a graph of f that includes the asymptotes. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

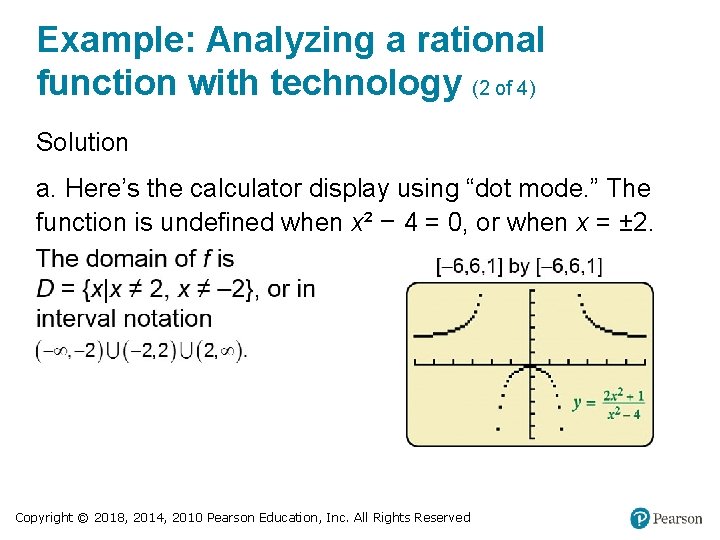
Example: Analyzing a rational function with technology (2 of 4) Solution a. Here’s the calculator display using “dot mode. ” The function is undefined when x² − 4 = 0, or when x = ± 2. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Analyzing a rational function with technology (3 of 4) Solution Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

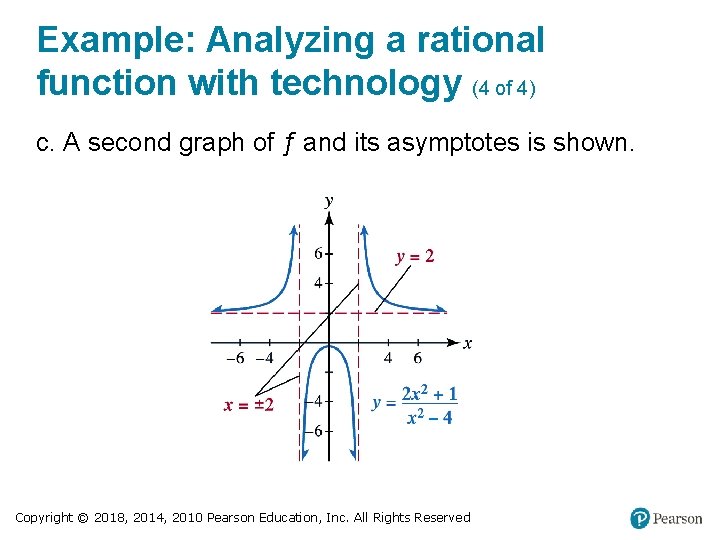
Example: Analyzing a rational function with technology (4 of 4) c. A second graph of ƒ and its asymptotes is shown. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Graphing a Rational Function (1 of 3) STEP 1: Find all vertical asymptotes. STEP 2: Find all horizontal or oblique asymptotes. STEP 3: Find the y-intercept, if possible, by evaluating f(0). Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Graphing a Rational Function (2 of 3) STEP 4: Find the x-intercepts, if any, by solving f(x) = 0. (These will be the zeros of the numerator p(x). ) STEP 5: Determine whether the graph will intersect its nonvertical asymptote y = b by solving f(x) = b, where b is the y-value of the horizontal asymptote, or by solving f(x) = mx + b, where y = mx + b is the equation of the oblique asymptote. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

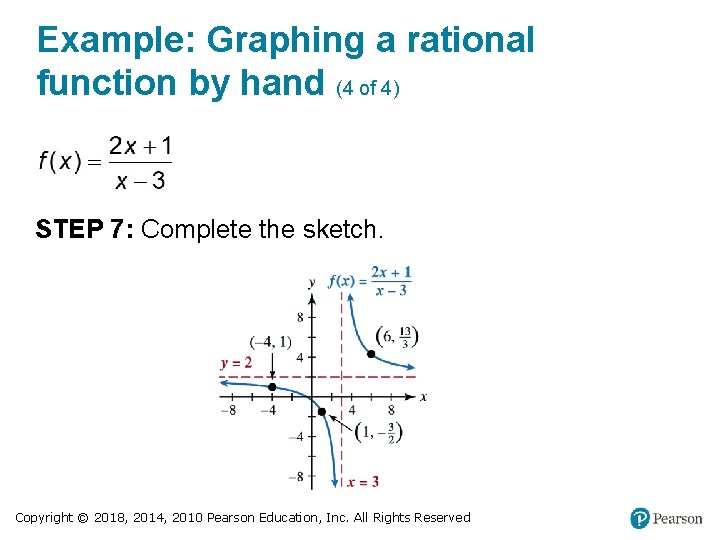
Graphing a Rational Function (3 of 3) STEP 6: Plot selected points as necessary. Choose an x-value in each interval of the domain determined by the vertical asymptotes and x-intercepts. STEP 7: Complete the sketch. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Graphing a rational function by hand (1 of 4) Solution STEP 1: The vertical asymptote has equation x = 3. STEP 2: The horizontal asymptote has equation y = 2. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Graphing a rational function by hand (2 of 4) STEP 4: Solve f(x) = 0 Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Graphing a rational function by hand (3 of 4) STEP 5: Graph does not intersect its horizontal asymptote, since f(x) = 2 has no solution. (Verify this. ) Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved

Example: Graphing a rational function by hand (4 of 4) STEP 7: Complete the sketch. Copyright © 2018, 2014, 2010 Pearson Education, Inc. All Rights Reserved