Rational Curve Rational curve Parametric representations using polynomials

Rational Curve

Rational curve • Parametric representations using polynomials are simply not powerful enough, because many curves (e. g. , circles, ellipses and hyperbolas) can not be obtained this way. • to overcome – use rational curve • What is rational curve?

Rational curve • Rational curve is defined by rational function. • Rational function ratio of two polynomial function. • Example • Parametric cubic Polynomial - x(u) = au 3 + bu 2 + cu + d • Rational parametric cubic polynomial - x(u) = axu 3 + bxu 2 + cxu + dx ahu 3 + bhu 2 + chu + dh

Rational curve • Use homogenous coordinate • E. g • Curve in 3 D space is represented by 4 coord (x, y, z, h). • Curve in 2 D plane is represented by 3 coord. (x, y, h). • Example (parametric quadratic polynomial in 2 D) • P = UA x(u) = axu 2 + bxu + cx y(u) = ayu 2 + byu + cy • P = [x, y] U = [u 2 , u, 1] A = ax • bx cx ay by cy

Rational curve • Rational parametric quadratic polynomial in 2 D • Ph = UAh h – homogenous coordinates • Ph = [hx, hy, h] • Matrix A (3 x 2) is now expand to 3 x 3 • ax Ah = bc x x ay ah by bh cy ch hx = axu 2 + bxu + cx hy = ayu 2 + byu + cy h = ahu 2 + bhu + ch

Rational curve • If h = 1 Ph = [x, y, 1] • 1 = h/h , x = hx/h, y = yh/h x(u) = axu 2 + bxu + cx ahu 2 + bhu + ch y(u) = ayu 2 + byu + cy ahu 2 + bhu + ch h = ahu 2 + bhu + ch = 1 ahu 2 + bhu + ch

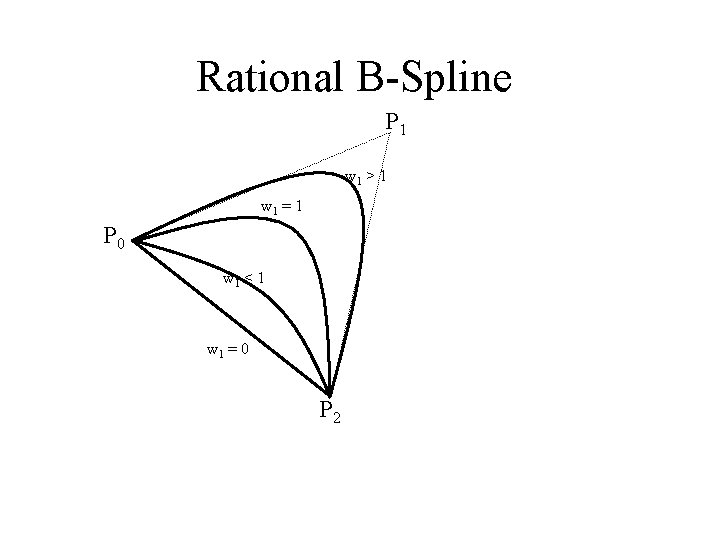
Rational B-Spline • B-Spline P(u) = Ni, k(u)pi • Rational B-Spline – P(u) = wi. Ni, k(u)pi – wi. Ni, k(u) – w weight factor shape parameters usually set by the designer to be nonnegative to ensure that the denominator is never zero.

Rational B-Spline • B-Spline P(u) = Ni, k(u)pi • Rational B-Spline – P(u) = wi. Ni, k(u)pi – wi. Ni, k(u) – The greater the value of a particular wi, the closer the curve is pulled toward the control point pi. – If all wi are set to the value 1 or all wi have the same value we have the standard B-Spline curve

Rational B-Spline • Example • To plot conic-section with rational B-spline, degree = 2 and 3 control points. • Knot vector = [0, 0, 0, 1, 1, 1] • Set weighting function • w 0 = w 2 = 1 • w 1 = r/ (1 -r) 0<= r <= 1

Rational B-Spline • Example (cont) • Rational B-Spline representation is • P(u) = p 0 N 0, 3+[r/(1 -r)] p 1 N 1, 3+ p 2 N 2, 3 N 0, 3+[r/(1 -r)] N 1, 3+ N 2, 3 We obtain the various conic with the following valued for parameter r r>1/2, w 1 > 1 hyperbola section r=1/2, w 1 = 1 parabola section r<1/2, w 1 < 1 ellipse section r=0, w 1 = 0 straight line section

Rational B-Spline P 1 w 1 > 1 w 1 = 1 P 0 w 1 < 1 w 1 = 0 P 2

Rational B-Spline : advantages • Can provide an exact representation for quadric curves (conic) such as circle and ellipse. • Invariant with respect to a perspective viewing transformation. we can apply a perspective viewing transformation to the control points and we will obtain the correct view of the curve.