Rational and Irrational 7 2 1 5 2004

Rational and Irrational 7 2 1 5 © 2004 All rights reserved

Rational and Irrational Numbers Rational Numbers a b A rational number is any number that can be expressed as the ratio of two integers. All terminating and repeating decimals can be expressed in this way so they are irrational numbers. Examples 4 5 2 8 2 = 3 3 7 0. 7 = 10 1 0. 3 = 3 6 6 = 1 0. 625 5 = 8 3 0. 27 = 11 -3 = - 3 1 2. 7 34. 56 27 = 10 3456 = 100 1 0. 142857 = 7

Rational and Irrational Numbers Rational Numbers A rational number is any number that can be expressed as the ratio of two integers. All terminating and repeating decimals can be expressed in this way so they are irrational numbers. a b Show that the terminating decimals below are rational. 0. 6 3. 8 56. 1 3. 45 2. 157 6 10 38 10 561 10 345 100 2157 1000 Rational

Rational and Irrational Numbers Rational Numbers A rational number is any number that can be expressed as the ratio of two integers. All terminating and repeating decimals can be expressed in this way so they are irrational numbers. a b To show that a repeating decimal is rational. Example 1 Example 2 To show that 0. 333… is rational. To show that 0. 4545… is rational. Let x = 0. 333… 10 x = 3. 33… 9 x = 3/9 x = 1/3 x = 0. 4545… 100 x = 45. 45… 99 x = 45/99 x = 5/11

Rational and Irrational Numbers Rational Numbers A rational number is any number that can be expressed as the ratio of two integers. All terminating and repeating decimals can be expressed in this way so they are irrational numbers. Question 1 a b Question 2 Show that 0. 222… is rational. Show that 0. 6363… is rational. Let x = 0. 222… 10 x = 2. 22… 9 x = 2/9 x = 0. 6363… 100 x = 63. 63… 99 x = 63/99 x = 7/11

Rational and Irrational Numbers Rational Numbers A rational number is any number that can be expressed as the ratio of two integers. All terminating and repeating decimals can be expressed in this way so they are irrational numbers. Question 3 Show that 0. 273 is rational. Let x = 0. 273 1000 x = 273 999 x = 273/999 x = 91/333 a b Question 4 Show that 0. 1234 is rational. Let x = 0. 1234 10000 x = 1234 9999 x = 1234/9999

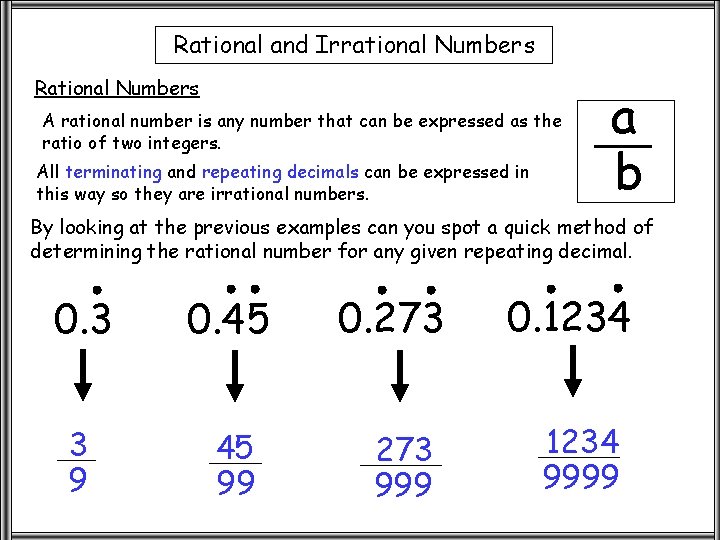
Rational and Irrational Numbers Rational Numbers A rational number is any number that can be expressed as the ratio of two integers. All terminating and repeating decimals can be expressed in this way so they are irrational numbers. a b By looking at the previous examples can you spot a quick method of determining the rational number for any given repeating decimal. 0. 3 0. 45 3 9 45 99 0. 273 999 0. 1234 9999

Rational and Irrational Numbers Rational Numbers A rational number is any number that can be expressed as the ratio of two integers. All terminating and repeating decimals can be expressed in this way so they are irrational numbers. a b Write the repeating part of the decimal as the numerator and write the denominator as a sequence of 9’s with the same number of digits as the numerator then simplify where necessary. 0. 3 0. 45 3 9 45 99 0. 273 999 0. 1234 9999

Rational and Irrational Numbers Rational Numbers A rational number is any number that can be expressed as the ratio of two integers. All terminating and repeating decimals can be expressed in this way so they are irrational numbers. a b Write down the rational form for each of the repeating decimals below. 0. 32 0. 7 0. 1543 0. 628 32 99 7 9 1543 9999 628 999

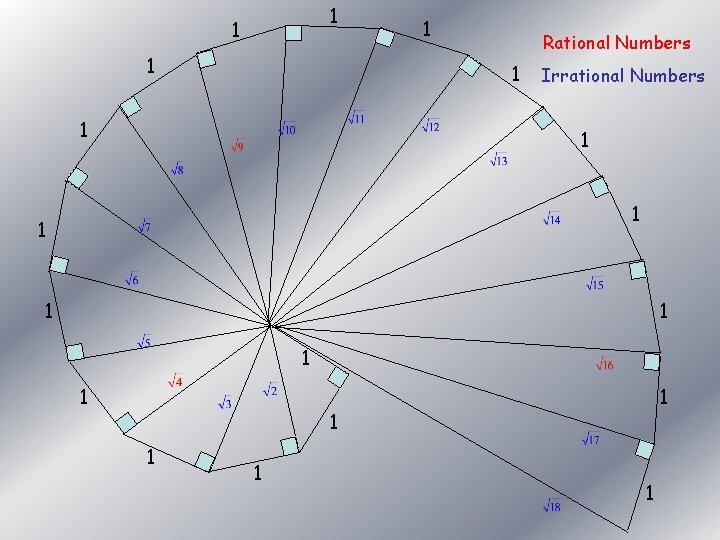
Irrational Rational and Irrational Numbers An irrational number is any number that cannot be expressed as the ratio of two integers. The history of irrational numbers begins with a discovery by the Pythagorean School in ancient Greece. A member of the school discovered that the diagonal of a unit square could not be expressed as the ratio of any two whole numbers. The motto of the school was “All is Number” (by which they meant whole numbers). Pythagoras believed in the absoluteness of whole numbers and could not accept the discovery. The member of the group that made it was Hippasus and he was sentenced to death by drowning. (See a b Pythagoras 1 slide 19/20 for more history) 1

1 1 Rational Numbers 1 1 Irrational Numbers 1 1 1

Rational and Irrational Numbers An irrational number is any number that cannot be expressed as the ratio of two integers. Intuition alone may convince you that all points on the “Real Number” line can be constructed from just the infinite set of rational numbers, after all between any two rational numbers we can always find another. It took mathematicians hundreds of years to show that the majority of Real Numbers are in fact irrational. The rationals and irrationals are needed together in order to complete the continuum that is the set of “Real Numbers”. a b Pythagoras 1 1

Rational and Irrational Numbers An irrational number is any number that cannot be expressed as the ratio of two integers. Surds are Irrational Numbers a b We can simplify numbers such as into rational numbers. However, other numbers involving roots such as those shown cannot be reduced to a rational form. Any number of the form Pythagoras which cannot be written as a rational number is called a surd. Other irrational numbers include and e, 1 (Euler’s number) All irrational numbers are non-terminating, non-repeating decimals. Their decimal expansion form shows no pattern whatsoever. 1

Rational and Irrational Numbers Multiplication and division of surds. For example: and also for example and

Rational and Irrational Numbers Example questions a Show that is rational b Show that is rational

Rational and Irrational Numbers Questions State whether each of the following are rational or irrational. a c b irrational h g rational irrational f e d rational irrational

Rational and Irrational Numbers Combining Rationals and Irrationals Addition and subtraction of an integer to an irrational number gives another irrational number, as does multiplication and division. Examples of irrationals

Rational and Irrational Numbers Combining Rationals and Irrationals Multiplication and division of an irrational number by another irrational can often lead to a rational number. Examples of Rationals 21 26 8 1 -13

Rational and Irrational Numbers Combining Rationals and Irrationals Determine whether the following are rational or irrational. (a) 0. 73 rational (f) (b) (c) 0. 666…. rational irrational (g) irrational (h) (k) irrational (e) irrational (i) rational irrational (j) (d) 3. 142 (j) rational irrational (l) rational

The Pythagoreans Pythagoras was a semi-mystical figure who was born on the Island of Samos in the Eastern Aegean in about 570 B. C. He travelled extensively throughout Egypt, Mesopotamia and India absorbing much mathematics and mysticism. He eventually settled in the Greek town of Crotona in southern Italy. Spirit Pythagoras He founded a secretive and scholarly society there that become Air known as the “Pythagorean Brotherhood”. It was a mystical almost religious society devoted to the study of Philosophy, Science and Mathematics. Their work was based on the belief that all natural phenomena could be explained by reference to whole numbers or ratios of whole numbers. Their motto became “All is Number”. They were successful in understanding the mathematical principals behind music. By examining the vibrations of a single string they discovered that harmonious tones only occurred when the string was fixed at points along its length that were ratios of whole numbers. For instance when a string is fixed 1/2 way along its length and plucked, a tone is produced that is 1 octave higher and in harmony with the original. Harmonious tones are produced when the string is fixed at distances such as 1/3, 1/4, 1/5, 2/3 and 3/4 of the way along its length. By fixing the string at points along its length that were not a simple fraction, a note is produced that is not in harmony with the other tones. History Water Earth Pentagram Fire

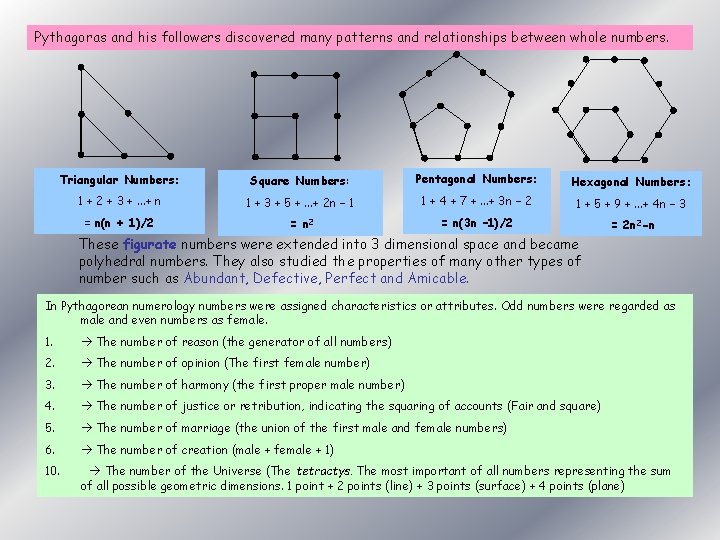
Pythagoras and his followers discovered many patterns and relationships between whole numbers. Triangular Numbers: Square Numbers: Pentagonal Numbers: Hexagonal Numbers: 1 + 2 + 3 +. . . + n 1 + 3 + 5 +. . . + 2 n – 1 1 + 4 + 7 +. . . + 3 n – 2 1 + 5 + 9 +. . . + 4 n – 3 = n(n + 1)/2 = n(3 n – 1)/2 = 2 n 2 -n These figurate numbers were extended into 3 dimensional space and became polyhedral numbers. They also studied the properties of many other types of number such as Abundant, Defective, Perfect and Amicable. In Pythagorean numerology numbers were assigned characteristics or attributes. Odd numbers were regarded as male and even numbers as female. 1. The number of reason (the generator of all numbers) 2. The number of opinion (The first female number) 3. The number of harmony (the first proper male number) 4. The number of justice or retribution, indicating the squaring of accounts (Fair and square) 5. The number of marriage (the union of the first male and female numbers) 6. The number of creation (male + female + 1) 10. The number of the Universe (The tetractys. The most important of all numbers representing the sum of all possible geometric dimensions. 1 point + 2 points (line) + 3 points (surface) + 4 points (plane)

The Square Root of 2 is Irrational This is a “reductio-ad-absurdum” proof. To prove that 1 is irrational Assume the contrary: 2 is rational 1 That is, there exist integers p and q with no common factors such that: (Since 2 q 2 is even, p 2 is even so p even) (odd 2 = odd) So p = 2 k for some k. (Since p is even, q 2 is even so q is even) So q = 2 m for some m. This contradicts the original assumption. is irrational. QED Proof