Ratio Combining Demonstration This resource provides animated demonstrations

Ratio – Combining – Demonstration This resource provides animated demonstrations of the mathematical method. Check animations and delete slides not needed for your class.

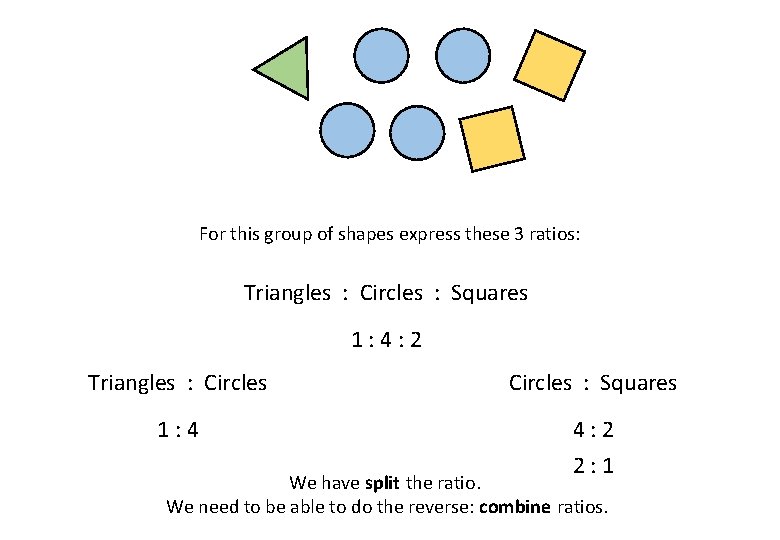
For this group of shapes express these 3 ratios: Triangles : Circles : Squares 1: 4: 2 Triangles : Circles : Squares 1: 4 4: 2 2: 1 We have split the ratio. We need to be able to do the reverse: combine ratios.

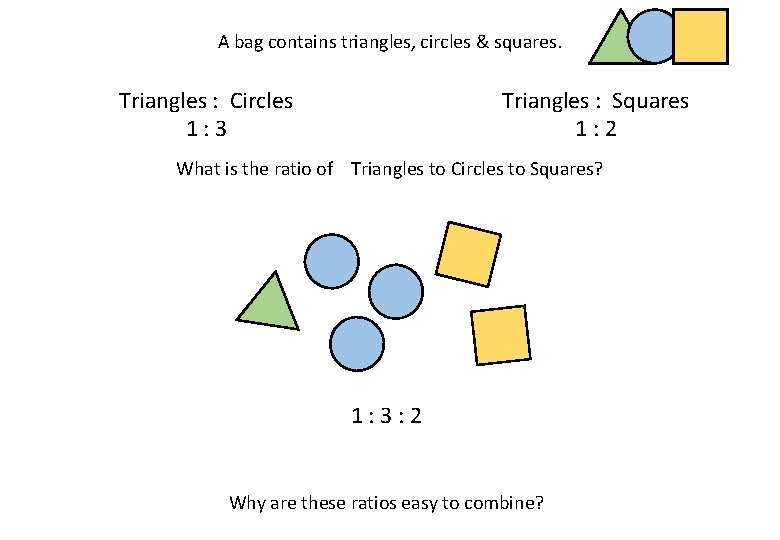
A bag contains triangles, circles & squares. Triangles : Circles 1: 3 Triangles : Squares 1: 2 What is the ratio of Triangles to Circles to Squares? 1: 3: 2 Why are these ratios easy to combine?

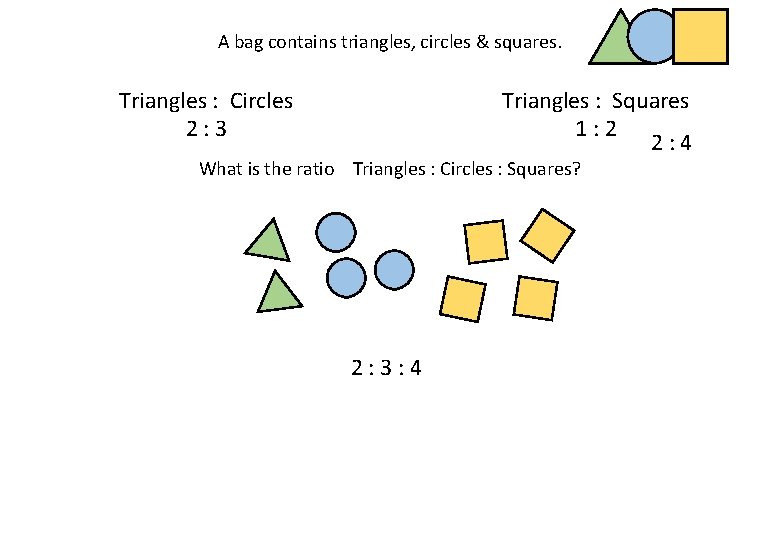
A bag contains triangles, circles & squares. Triangles : Circles 2: 3 Triangles : Squares 1: 2 2: 4 What is the ratio Triangles : Circles : Squares? 2: 3: 4

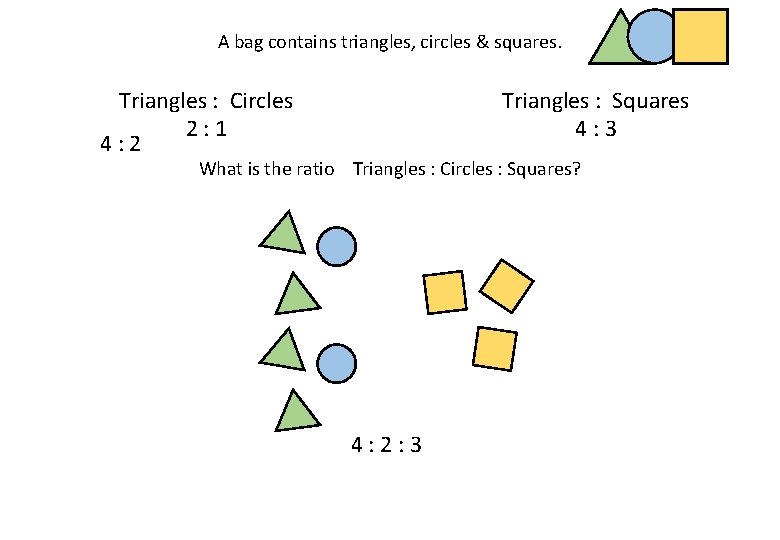
A bag contains triangles, circles & squares. Triangles : Circles 2: 1 4: 2 Triangles : Squares 4: 3 What is the ratio Triangles : Circles : Squares? 4: 2: 3

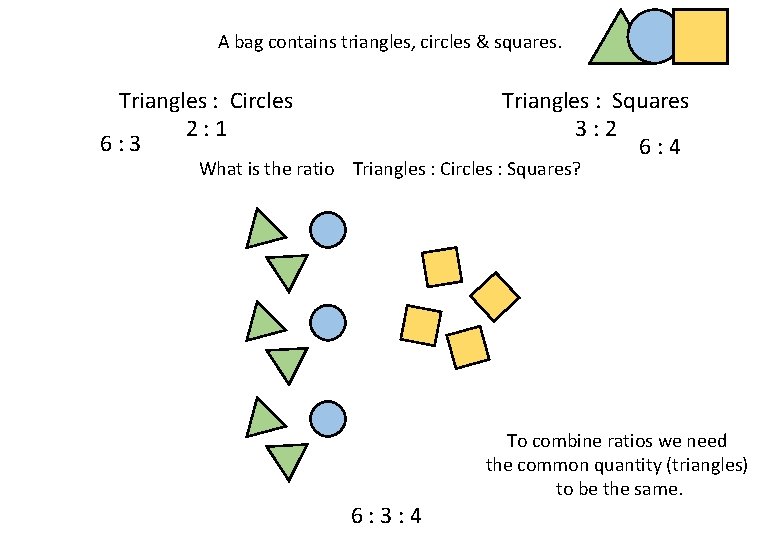
A bag contains triangles, circles & squares. Triangles : Circles 2: 1 6: 3 Triangles : Squares 3: 2 6: 4 What is the ratio Triangles : Circles : Squares? 6: 3: 4 To combine ratios we need the common quantity (triangles) to be the same.

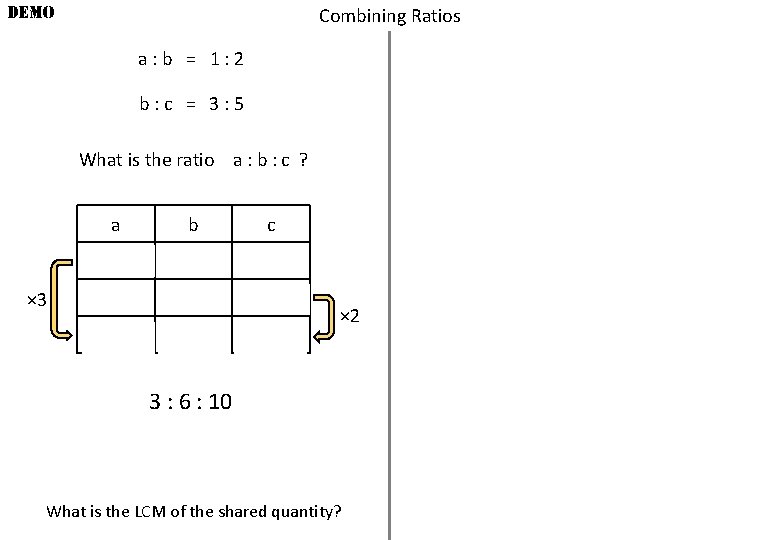
DEMO Combining Ratios a: b = 1: 2 b: c = 3: 5 What is the ratio a : b : c ? a b 1 2 × 3 3 c 3 5 6 10 × 2 3 : 6 : 10 What is the LCM of the shared quantity?

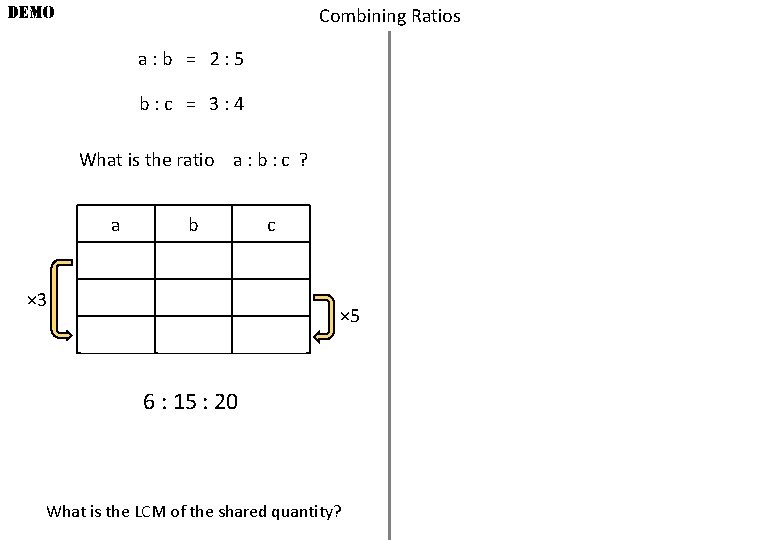
DEMO Combining Ratios a: b = 2: 5 b: c = 3: 4 What is the ratio a : b : c ? a b 2 5 × 3 6 c 3 4 15 20 × 5 6 : 15 : 20 What is the LCM of the shared quantity?

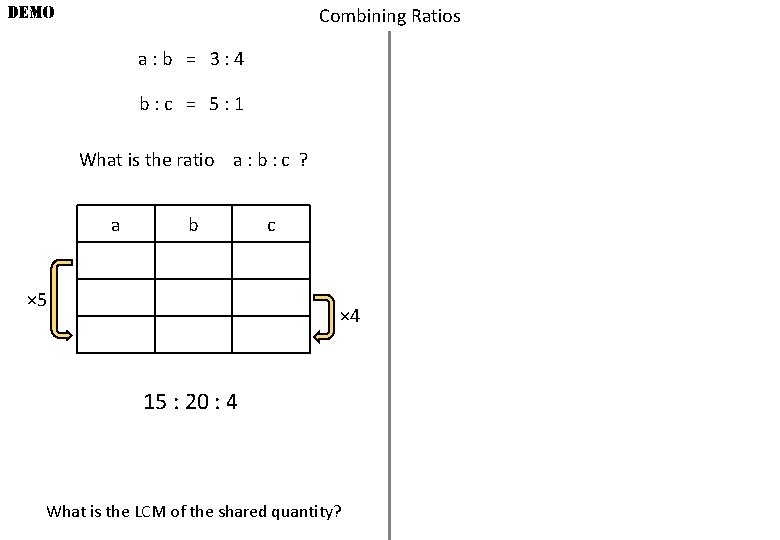
DEMO Combining Ratios a: b = 3: 4 b: c = 5: 1 What is the ratio a : b : c ? a b 3 4 × 5 15 c 5 1 20 4 × 4 15 : 20 : 4 What is the LCM of the shared quantity?

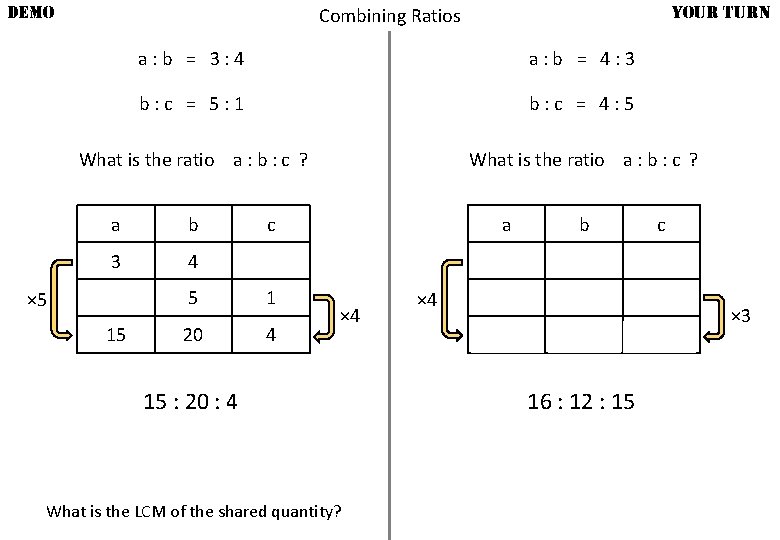
DEMO YOUR TURN Combining Ratios a: b = 3: 4 a: b = 4: 3 b: c = 5: 1 b: c = 4: 5 What is the ratio a : b : c ? a b 3 4 × 5 15 c 5 1 20 4 × 4 15 : 20 : 4 What is the LCM of the shared quantity? a b 4 3 × 4 16 c 4 5 12 15 16 : 12 : 15 × 3

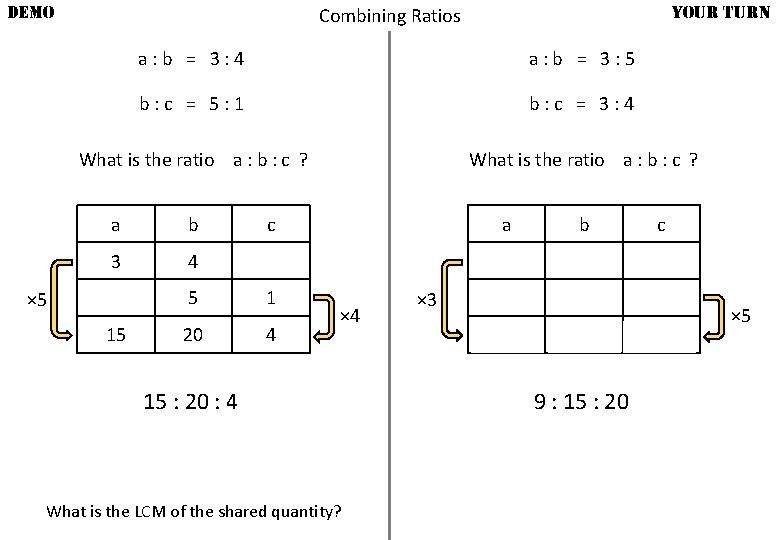
DEMO YOUR TURN Combining Ratios a: b = 3: 4 a: b = 3: 5 b: c = 5: 1 b: c = 3: 4 What is the ratio a : b : c ? a b 3 4 × 5 15 c 5 1 20 4 × 4 15 : 20 : 4 What is the LCM of the shared quantity? a b 3 5 × 3 9 c 3 4 15 20 9 : 15 : 20 × 5

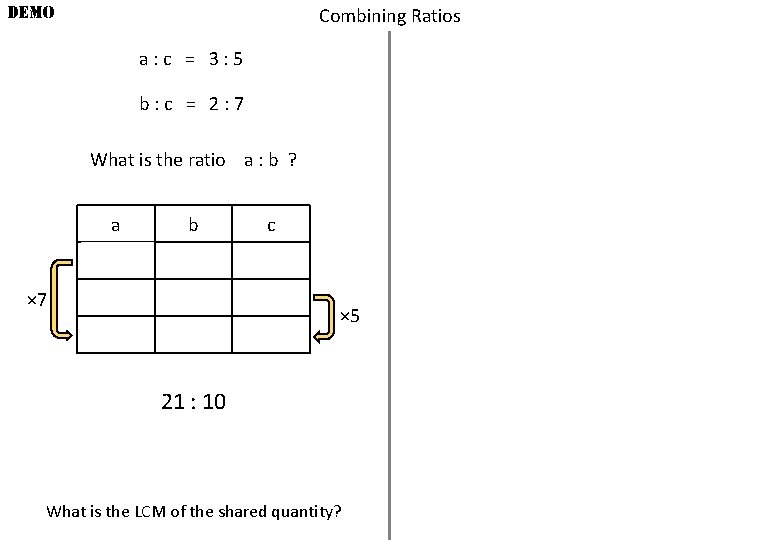
DEMO Combining Ratios a: c = 3: 5 b: c = 2: 7 What is the ratio a : b ? a b 3 × 7 21 c 5 2 7 10 35 × 5 21 : 10 What is the LCM of the shared quantity?

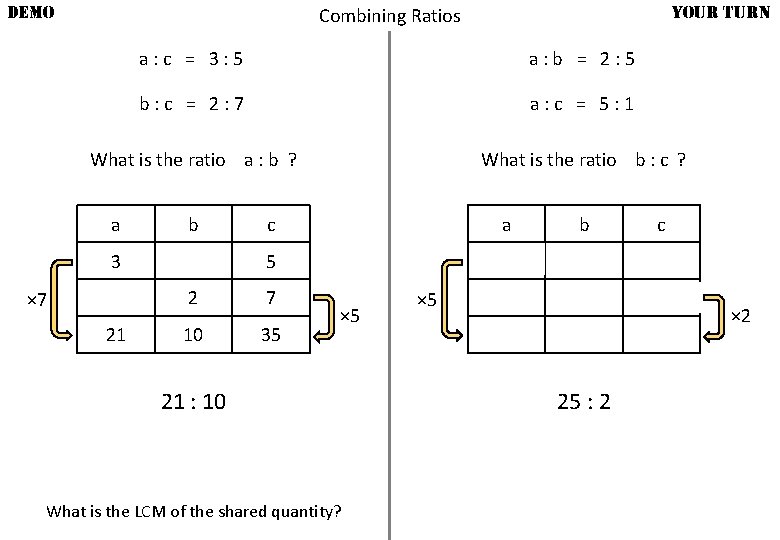
DEMO YOUR TURN Combining Ratios a: c = 3: 5 a: b = 2: 5 b: c = 2: 7 a: c = 5: 1 What is the ratio a : b ? What is the ratio b : c ? a b 3 × 7 21 c a b 5 2 7 10 35 × 5 21 : 10 What is the LCM of the shared quantity? × 5 5 10 c 1 25 25 : 2 2 × 2

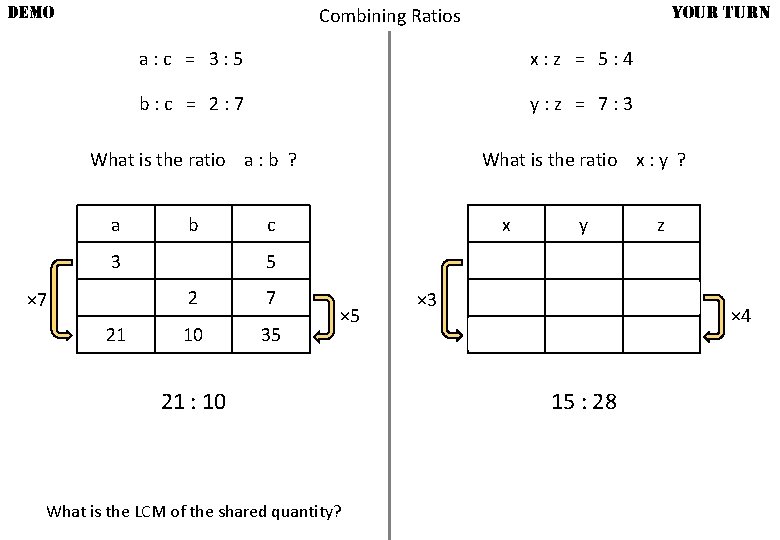
DEMO YOUR TURN Combining Ratios a: c = 3: 5 x: z = 5: 4 b: c = 2: 7 y: z = 7: 3 What is the ratio a : b ? What is the ratio x : y ? a b 3 × 7 21 c x 5 5 2 7 10 35 × 5 21 : 10 What is the LCM of the shared quantity? × 3 15 y z 4 7 3 28 12 15 : 28 × 4

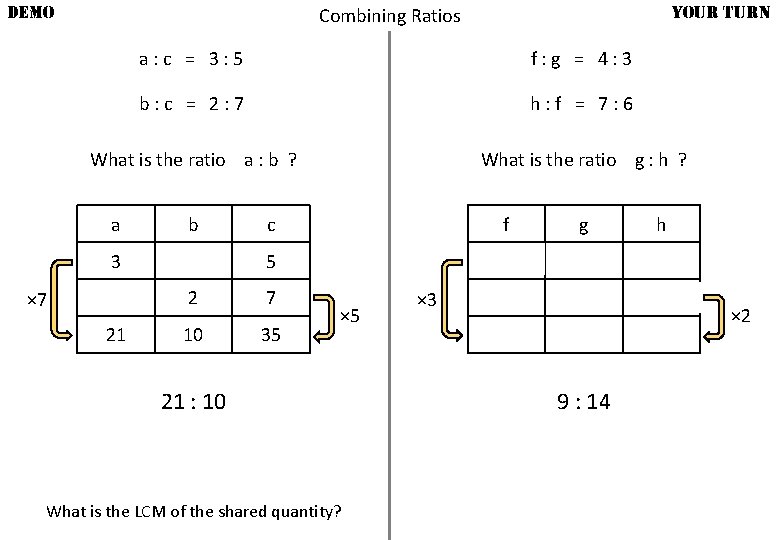
DEMO YOUR TURN Combining Ratios a: c = 3: 5 f: g = 4: 3 b: c = 2: 7 h: f = 7: 6 What is the ratio a : b ? What is the ratio g : h ? a b 3 × 7 21 c f g 5 4 3 2 7 10 35 × 5 21 : 10 What is the LCM of the shared quantity? × 3 6 12 h 7 9 9 : 14 14 × 2

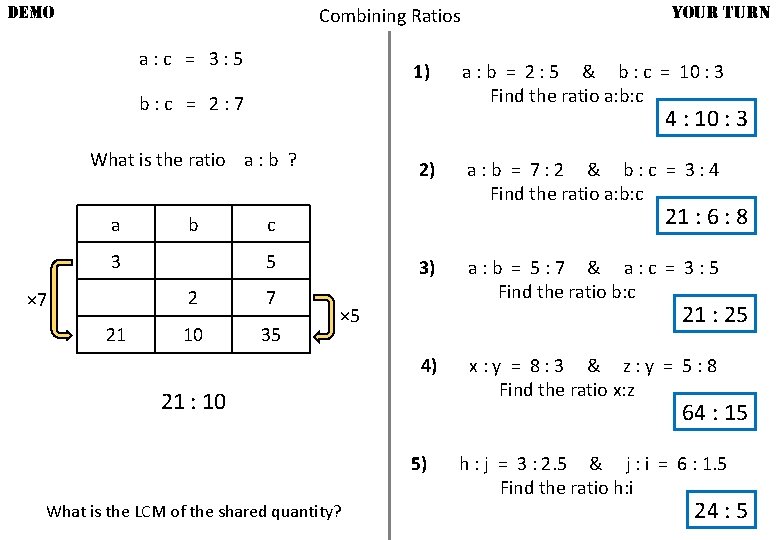
DEMO Combining Ratios a: c = 3: 5 1) b: c = 2: 7 b 3 × 7 21 a : b = 2 : 5 & b : c = 10 : 3 Find the ratio a: b: c 4 : 10 : 3 What is the ratio a : b ? a YOUR TURN 2) 21 : 6 : 8 c 5 2 7 10 35 a: b = 7: 2 & b: c = 3: 4 Find the ratio a: b: c 3) 21 : 25 × 5 4) 21 : 10 x: y = 8: 3 & z: y = 5: 8 Find the ratio x: z 64 : 15 5) What is the LCM of the shared quantity? a: b = 5: 7 & a: c = 3: 5 Find the ratio b: c h : j = 3 : 2. 5 & j : i = 6 : 1. 5 Find the ratio h: i 24 : 5

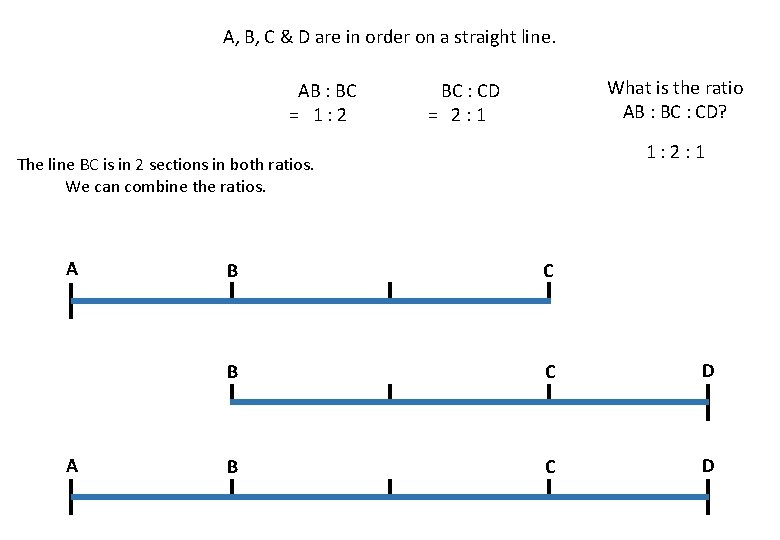
A, B, C & D are in order on a straight line. AB : BC = 1: 2 What is the ratio AB : BC : CD? BC : CD = 2: 1 1: 2: 1 The line BC is in 2 sections in both ratios. We can combine the ratios. A A B C D

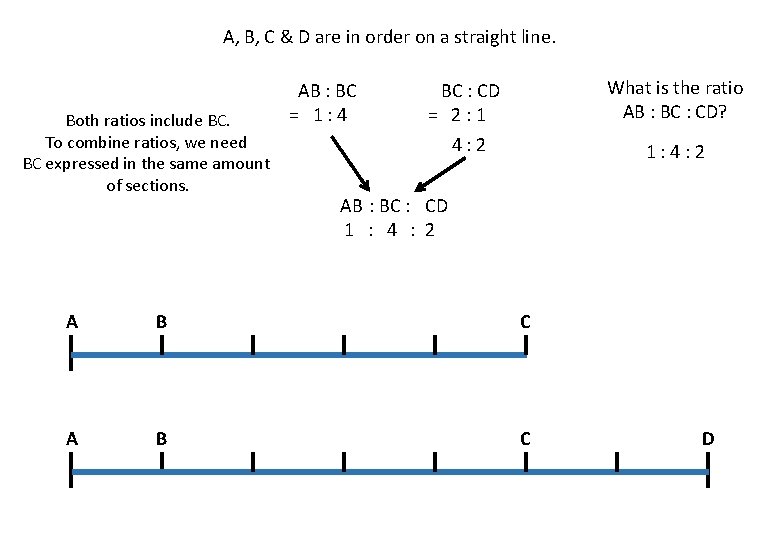
A, B, C & D are in order on a straight line. Both ratios include BC. To combine ratios, we need BC expressed in the same amount of sections. AB : BC = 1: 4 What is the ratio AB : BC : CD? BC : CD = 2: 1 4: 2 1: 4: 2 AB : BC : CD 1 : 4 : 2 A B C D

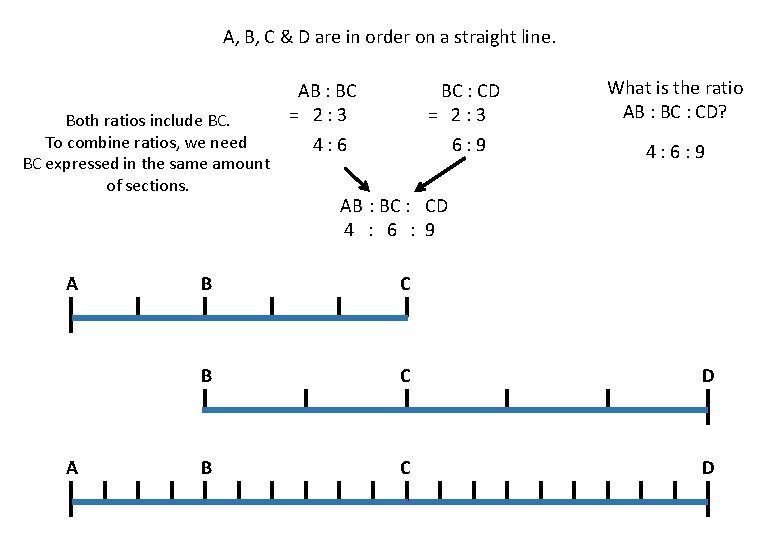
A, B, C & D are in order on a straight line. Both ratios include BC. To combine ratios, we need BC expressed in the same amount of sections. A A AB : BC = 2: 3 4: 6 BC : CD = 2: 3 6: 9 What is the ratio AB : BC : CD? 4: 6: 9 AB : BC : CD 4 : 6 : 9 B C D

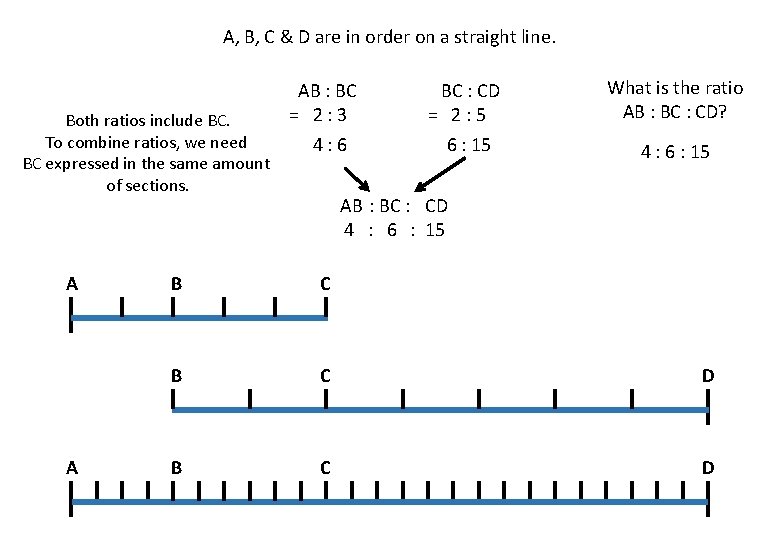
A, B, C & D are in order on a straight line. Both ratios include BC. To combine ratios, we need BC expressed in the same amount of sections. A A AB : BC = 2: 3 4: 6 BC : CD = 2: 5 6 : 15 What is the ratio AB : BC : CD? 4 : 6 : 15 AB : BC : CD 4 : 6 : 15 B C D

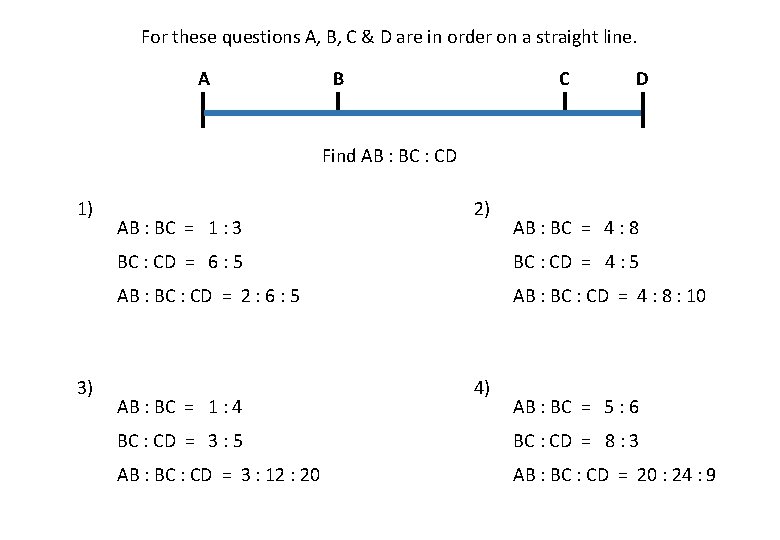
For these questions A, B, C & D are in order on a straight line. A B C D Find AB : BC : CD 1) 3) AB : BC = 1 : 3 2) AB : BC = 4 : 8 BC : CD = 6 : 5 BC : CD = 4 : 5 AB : BC : CD = 2 : 6 : 5 AB : BC : CD = 4 : 8 : 10 AB : BC = 1 : 4 4) AB : BC = 5 : 6 BC : CD = 3 : 5 BC : CD = 8 : 3 AB : BC : CD = 3 : 12 : 20 AB : BC : CD = 20 : 24 : 9

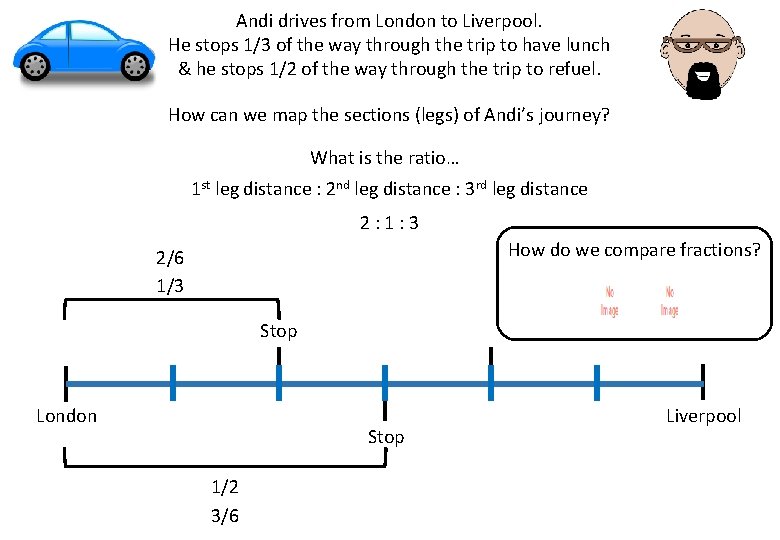
Andi drives from London to Liverpool. He stops 1/3 of the way through the trip to have lunch & he stops 1/2 of the way through the trip to refuel. How can we map the sections (legs) of Andi’s journey? What is the ratio… 1 st leg distance : 2 nd leg distance : 3 rd leg distance 2: 1: 3 How do we compare fractions? 2/6 1/3 Stop London Stop 1/2 3/6 Liverpool

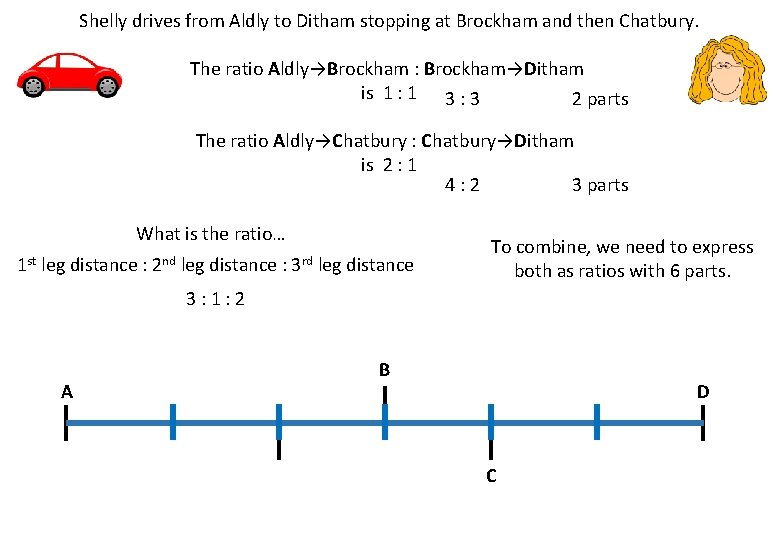
Shelly drives from Aldly to Ditham stopping at Brockham and then Chatbury. The ratio Aldly→Brockham : Brockham→Ditham is 1 : 1 3 : 3 2 parts The ratio Aldly→Chatbury : Chatbury→Ditham is 2 : 1 4: 2 3 parts What is the ratio… 1 st leg distance : 2 nd leg distance : 3 rd leg distance To combine, we need to express both as ratios with 6 parts. 3: 1: 2 A B D C

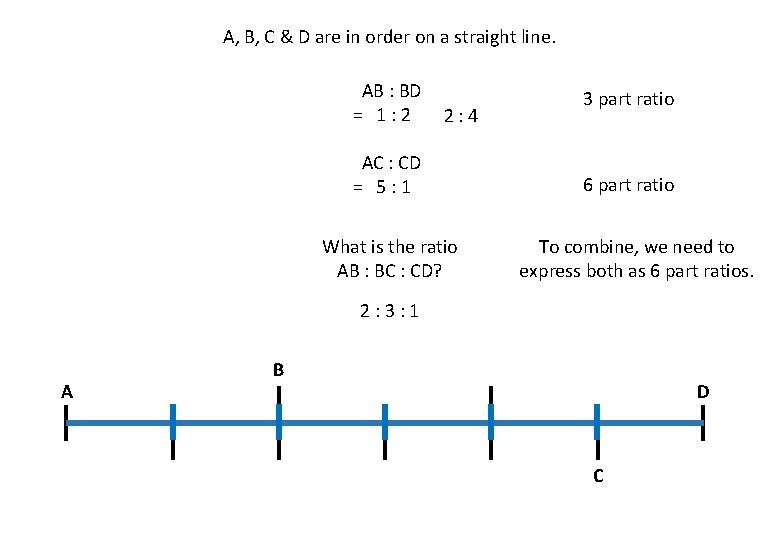
A, B, C & D are in order on a straight line. AB : BD = 1: 2 2: 4 AC : CD = 5: 1 What is the ratio AB : BC : CD? 3 part ratio 6 part ratio To combine, we need to express both as 6 part ratios. 2: 3: 1 A B D C

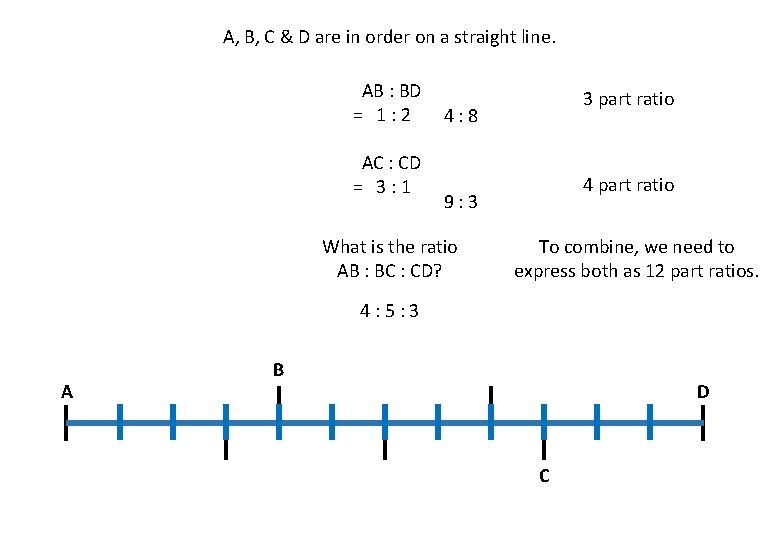
A, B, C & D are in order on a straight line. AB : BD = 1: 2 AC : CD = 3: 1 3 part ratio 4: 8 4 part ratio 9: 3 What is the ratio AB : BC : CD? To combine, we need to express both as 12 part ratios. 4: 5: 3 A B D C

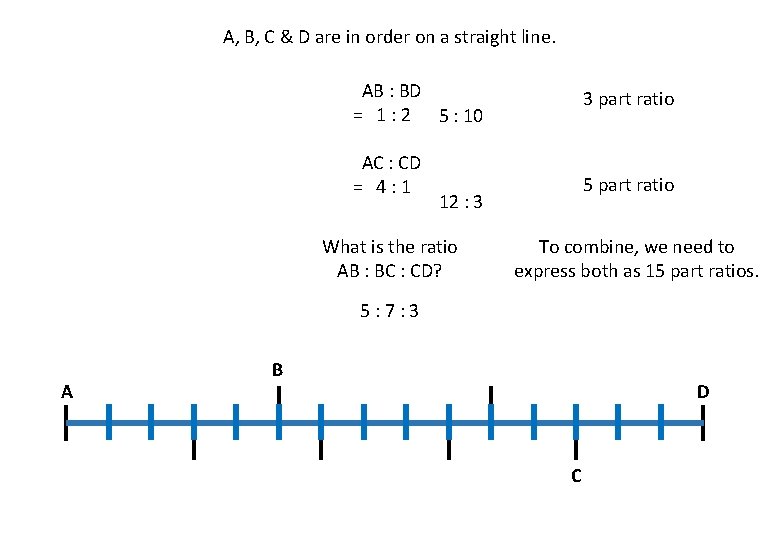
A, B, C & D are in order on a straight line. AB : BD = 1 : 2 5 : 10 3 part ratio AC : CD = 4: 1 5 part ratio 12 : 3 What is the ratio AB : BC : CD? To combine, we need to express both as 15 part ratios. 5: 7: 3 A B D C

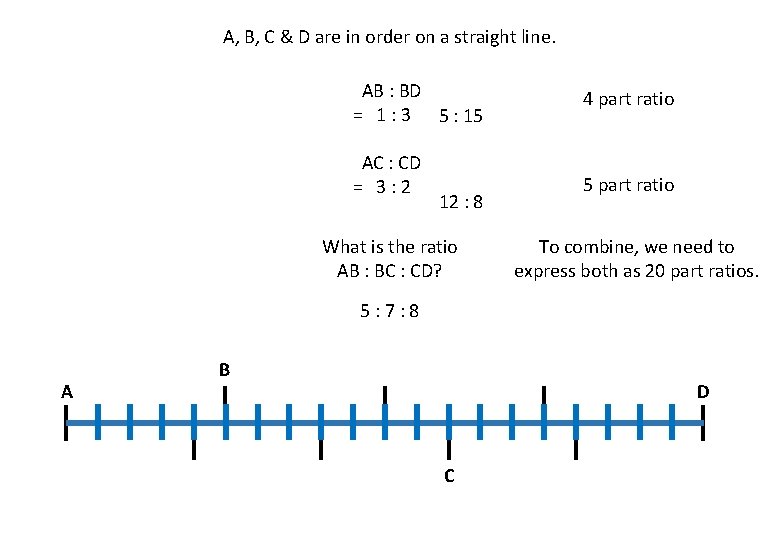
A, B, C & D are in order on a straight line. AB : BD = 1 : 3 5 : 15 4 part ratio AC : CD = 3: 2 5 part ratio 12 : 8 What is the ratio AB : BC : CD? To combine, we need to express both as 20 part ratios. 5: 7: 8 A B D C

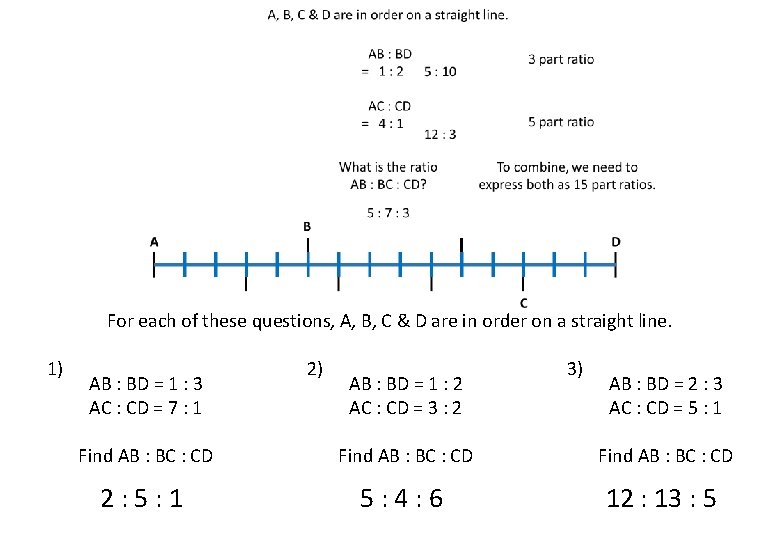
For each of these questions, A, B, C & D are in order on a straight line. 1) AB : BD = 1 : 3 AC : CD = 7 : 1 2) AB : BD = 1 : 2 AC : CD = 3 : 2 3) AB : BD = 2 : 3 AC : CD = 5 : 1 Find AB : BC : CD 2: 5: 1 5: 4: 6 12 : 13 : 5

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk