Rate of change Differentiation Gradient of curves Differentiating

Rate of change / Differentiation • Gradient of curves • Differentiating • Maxima and Minima • Optimisation

Topic 7 : Introduction to Differential Calculus

Lesson 1 Do Now #1 #2 #3 #4 Topic 7 : Introduction to Differential Calculus

Answer #1 Answer #2 Answer #3 Answer #4 Topic 7 : Introduction to Differential Calculus

Recall: A bit of symbology y x dy dx = “difference in y” = gradient of line “difference in x” PRONOUNCED “dee-why by dee-ex”

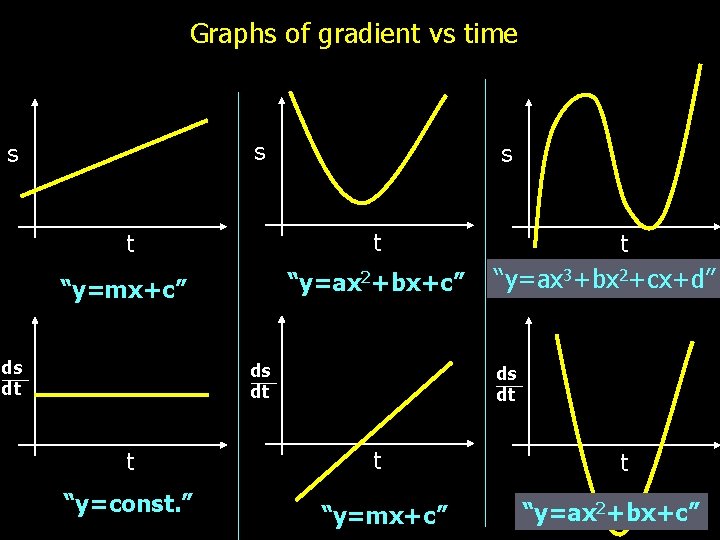
Graphs of gradient vs time s s s t t “y=mx+c” “y=ax 2+bx+c” ds dt t “y=ax 3+bx 2+cx+d” ds dt t t “y=const. ” “y=mx+c” t “y=ax 2+bx+c”

Introduction to Applications Topic 7 : Introduction to Differential Calculus

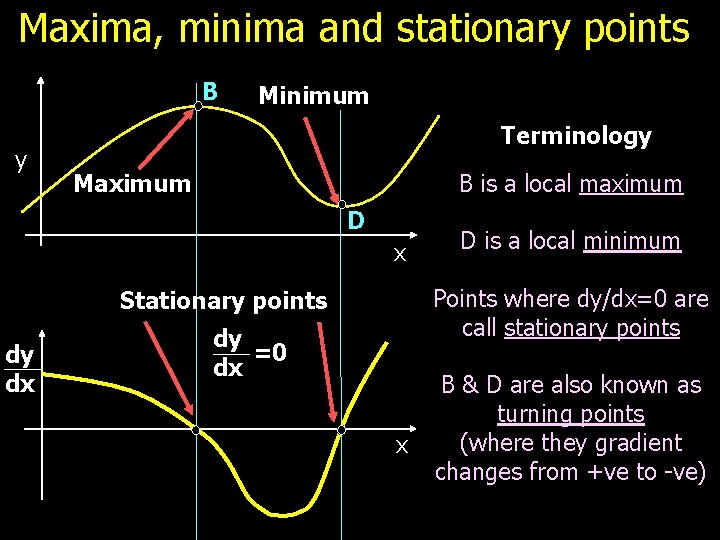
Maxima, minima and stationary points B y Minimum Terminology B is a local maximum Maximum D x Points where dy/dx=0 are call stationary points Stationary points dy dx D is a local minimum dy =0 dx x B & D are also known as turning points (where they gradient changes from +ve to -ve)

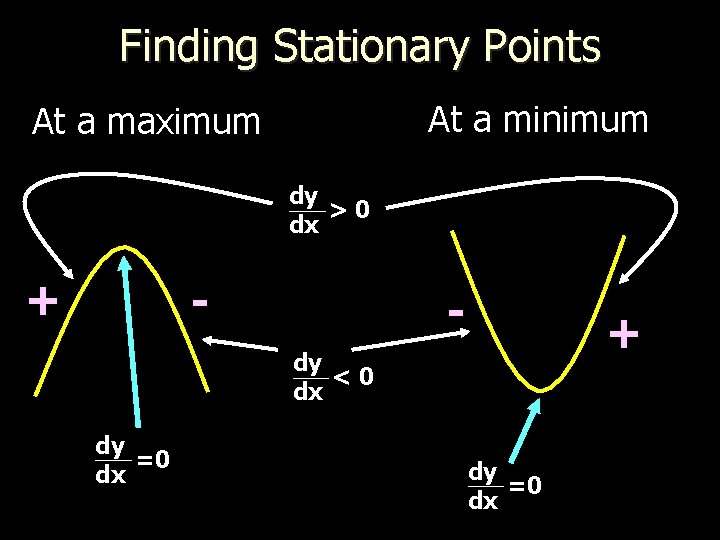
Finding Stationary Points At a minimum At a maximum dy >0 dx + - - + dy <0 dx dy =0 dx

Example f(x)= x 3 - 12 x + 1 “Find stationary points and determine their types” f’(x)= 3 x 2 - 12 Stationary points occur when gradient [derivative] is 0 3 x 2 - 12 = 0 3 x 2 = 12 x 2 = 4 x = 2 or x = When x = -2 Pick point to left (x = -2. 1) f`(x) = 3 x(-2. 1)2 -12 = 1. 23 [+ve] When x = +2 Pick point to left (x = 1. 9) f`(x) = 3 x(1. 9)2 -12 = -1. 17 [-ve] Pick point to right (x = 2. 1) (x = -1. 9) f`(x) = 3 x(2. 1)2 -12 f`(x) = 3 x(-1. 9)2 -12 = 1. 23 [+ve] = -1. 17 [-ve] -2 -ve +ve -ve Minimum Maximum

Example (continued) f(x)= x 3 f’(x)= 3 x 2 - 12 x + 1 “… and sketch the graph” Stationary points When x = -2 +ve -ve Maximum When x = +2 -ve +ve When x=0 [y-axis] y = (-2)3 -12(-2) +1 = -8 + 24 + 1 = 17 Minimum y = 03 -12 x 0 +1 =1 y = (2)3 -12(2) +1 = 8 - 24 + 1 (0, 1) = -15 Maximum at (-2, 17) Minimum at (2, -15)

Example (continued) f(x)= x 3 - 12 x + 1 Crosses y-axis at (0, 1) Cubic function Maximum at (-2, 17) Y 20 X Try Page 125 Ex A Q 1 -2 -20 2 Minimum at (2, -15)

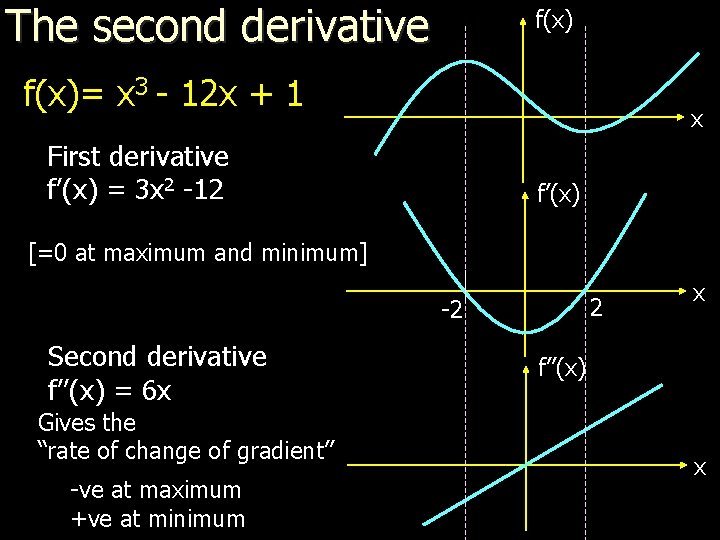
The second derivative f(x)= x 3 - 12 x + 1 x First derivative f’(x) = 3 x 2 -12 f’(x) [=0 at maximum and minimum] 2 -2 Second derivative f’’(x) = 6 x Gives the “rate of change of gradient” -ve at maximum +ve at minimum x f’’(x) x

The second derivative KEY POINTS 2 y d The second derivative is denoted by dx 2 . . for a function p(x) it is denoted by p’’(x) It is used at a simple way of telling if a stationary point is a maximum or a minimum 2 y d If is negative then the stationary point is a maximum 2 dx d 2 y If is positive then the stationary point is a minimum 2 dx

The second derivative - example f(x) = 1/ 3 x 3 - 2 x 2 + 3 x +1 “Find stationary points and determine their nature” f’(x) = x 2 - 4 x + 3 Stationary points when f’(x)=0 x 2 - 4 x + 3 = 0 (x - 3)(x - 1) = 0 x = 3 and x = 1 are maxima or minima Look at the second derivative to determine their nature f’’(x) = 2 x - 4 When x=3 f’’(x) = 2 x 3 - 4 = 2 which is positive … hence a minimum When x=1 f’’(x) = 2 x 1 - 4 = -2 which is negative … hence a maximum

The second derivative - Exam Q f(x) = 4 x 3 - 9 x 2 - 30 x +1 “Find stationary points and determine their nature” f’(x) = 12 x 2 - 18 x - 30 = 0 Stationary points when f’(x)=0 2 x 2 - 3 x - 5 = 0 (2 x - 5)(x + 1) = 0 x = 2. 5 and x = -1 are maxima or minima Look at the second derivative to determine their nature f’’(x) = 24 x - 18 When x=2. 5 f’’(x) = 24 x 2. 5 - 18 = 42 which is positive … hence a minimum When x=-1 f’’(x) = 24 x-1 - 18 = -42 which is negative … hence a maximum