Rate Law Chapter 3 Rate Law Objectives Part

Rate Law Chapter 3

Rate Law: Objectives Part I • Write the relationship between the relative rates of reaction. • Write a rate law and define reaction order and activation energy. Part II • Set up a stoichiometric table for both batch and flow systems and express concentration as a function or conversion. • Write -r. A solely as a function of conversion given the rate law and then entering concentration. • Calculate the equilibrium conversion for both gas and liquid phase reactions.

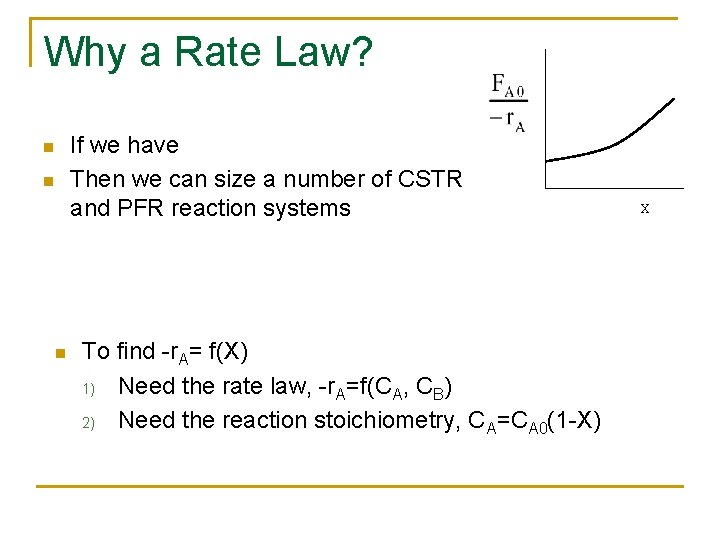
Why a Rate Law? n n n If we have Then we can size a number of CSTR and PFR reaction systems To find -r. A= f(X) 1) Need the rate law, -r. A=f(CA, CB) 2) Need the reaction stoichiometry, CA=CA 0(1 -X) X

Rate Law Basics n A rate law describes the behavior of a reaction. The rate of a reaction is a function of temperature (through the rate constant) and concentration. n Power Law Model n q k is the specific reaction rate (constant)

Elementary rate law n A reaction follows an elementary rate law if and only if the stoichiometric coefficients are the same as the individual reaction order of each species. n For the reaction in the previous example, n The rate law would be:

Non-Elementary Rate Laws If the rate law for the non-elementary reaction is may found to be then the reaction is said to be 2 nd order in A, 1 st order in B, and order overall is 2+1 =3 (3 rd order).

Rate Law Basics Consider the general equation The relative rate of reaction of the various species involved in the reaction can be obtained from the ratio of the stoichiometric coefficients. For every mole of A consumed c/a moles of C appears. Rate of formation of C= (c/a) rate of disappearance of A. The relationship can be expressed directly from the stoichiometry of the reaction

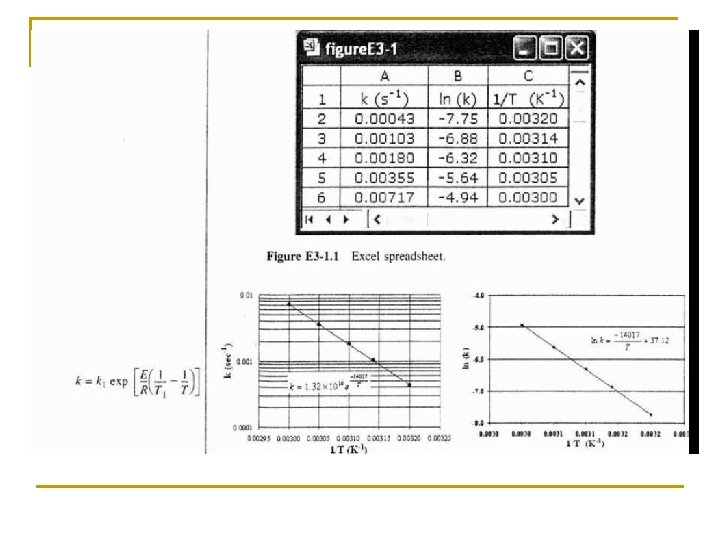
Rate Law Basics k is given by the Arrhenius Equation: q q q Where: E = activation energy (cal/mol) R = gas constant (cal/mol*K) T = temperature (K) A = frequency factor (units of A, and k, depend on overall reaction order)

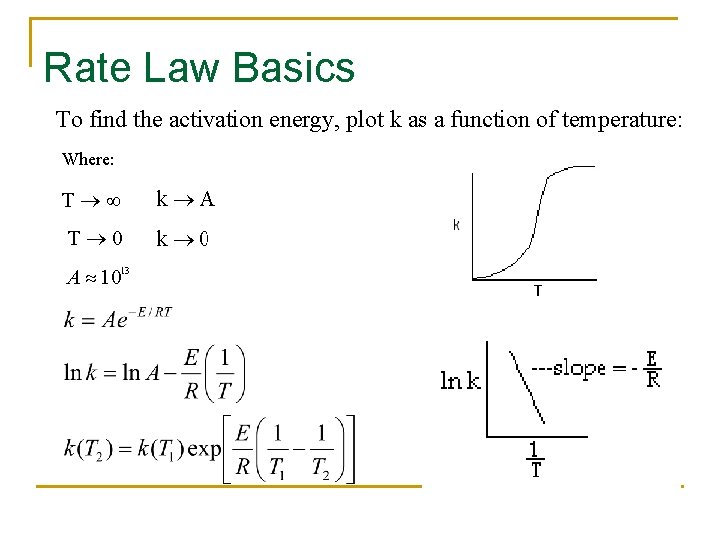
Rate Law Basics To find the activation energy, plot k as a function of temperature: Where:

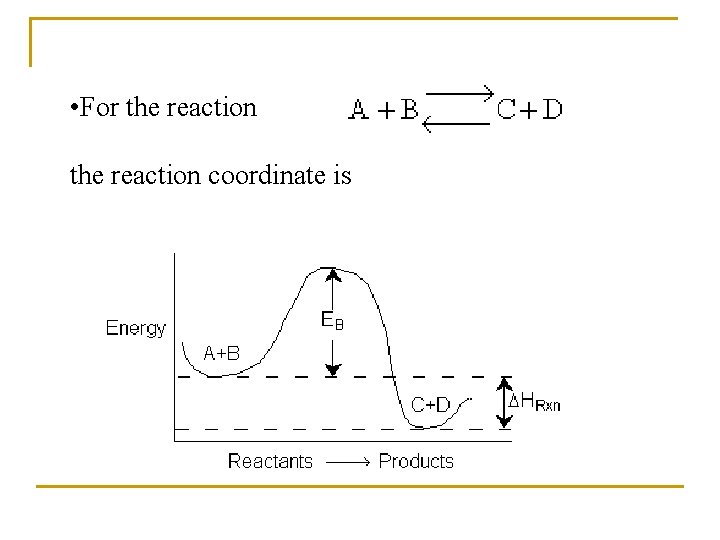
• For the reaction coordinate is

Activation Energy n n The activation energy can be thought of as a barrier to the reaction. One way to view the barrier to a reaction is through the reaction coordinates. These coordinates denote the energy of the system as a function of progress along the reaction path.

We see that for the reaction to occur, the reactants must overcome an energy barrier EB. The energy barrier is related to the activation energy, E. The barrier height is a result of (1) the molecules needing energy to distort or stretch their bonds in order to break them and to thus form new bonds, (2) the reaction molecules come close together they must overcome both steric and electron repulsion forces, and (3) the quantum effects that can in some cases produce a barrier.

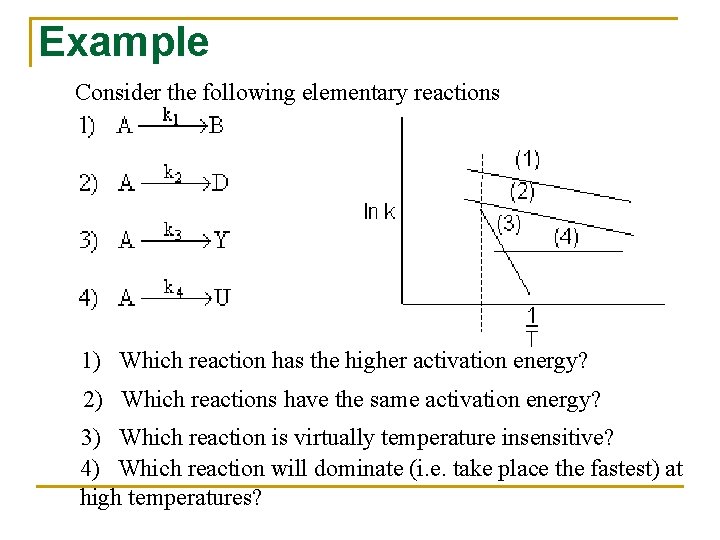
Example Consider the following elementary reactions 1) Which reaction has the higher activation energy? 2) Which reactions have the same activation energy? 3) Which reaction is virtually temperature insensitive? 4) Which reaction will dominate (i. e. take place the fastest) at high temperatures?

Reaction Order n You can tell the overall reaction order by the units of k CA -r. A (mol/dm 3) (mol/dm 3*s) Reaction Order Rate Law k zero -r. A = k (mol /dm 3*s) 1 st -r. A = k. C A s -1 2 nd -r. A = k. C A 2 (dm 3/mol*s)

Examples of Rate Laws • First Order Reactions (1) Homogeneous irreversible elementary gas phase reaction (2) Homogeneous reversible elementary reaction

Examples of Rate Laws Second Order Reactions (1) Homogeneous irreversible non-elementary reaction At 188˚C This is first order in ONCB, first order in ammonia and overall second order.

Examples of Rate Laws • Second Order Reactions (2) Homogeneous irreversible elementary reaction This reaction is first order in CNBr, first order in CH 3 NH 2 and overall second order.

Examples of Rate Laws (3) Heterogeneous catalytic reaction: The following reaction takes place over a solid catalyst:

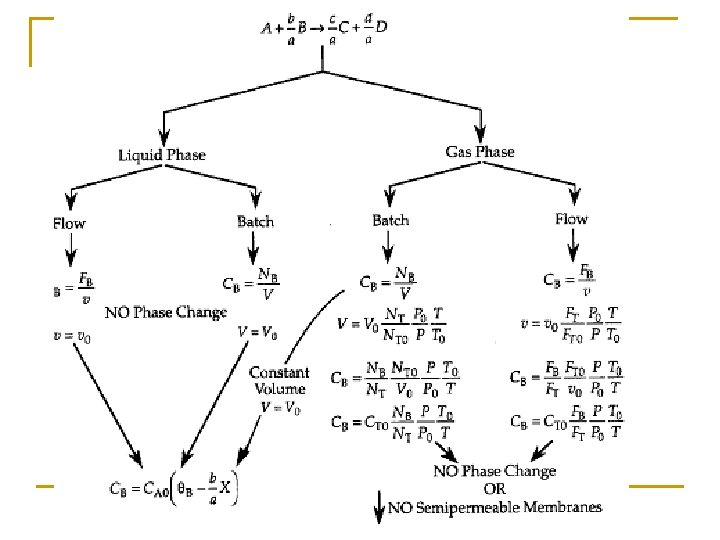
Stoichiometry n n n If the rate law depends on more than one species we must relate the concentrations of different species to each other This relationship is most easily established with the aid of a stoichiometric table The stoichiometric table presents the stoichiometric relationship between reacting molecules for a single reaction

Reaction Stoichiometry The relative rate of reaction of the various species involved in the reaction can be obtained from the ratio of the stoichiometric coefficients. For every mole of A consumed c/a moles of C appears. Rate of formation of C= (c/a) × rate of disappearance of A The relationship can be expressed directly from the stoichiometry of the reaction

Batch Stoichiometric Table t=0 t=t NA 0 NA NB 0 NB NC 0 NC ND 0 ND NI 0 NI

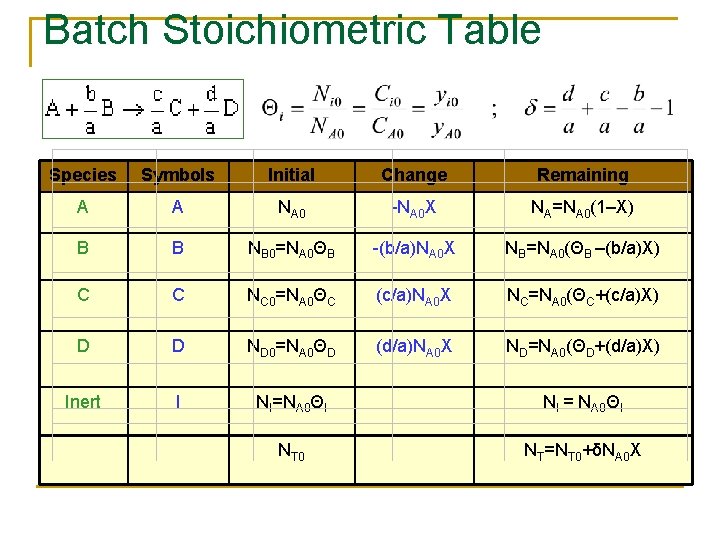
Batch Stoichiometric Table Species Symbols Initial Change Remaining A A NA 0 -NA 0 X NA=NA 0(1–X) B B NB 0=NA 0ΘB -(b/a)NA 0 X NB=NA 0(ΘB –(b/a)X) C C NC 0=NA 0ΘC (c/a)NA 0 X NC=NA 0(ΘC+(c/a)X) D D ND 0=NA 0ΘD (d/a)NA 0 X ND=NA 0(ΘD+(d/a)X) Inert I NI=NA 0ΘI NI = NA 0ΘI NT 0 NT=NT 0+δNA 0 X

Concentration: Batch Constant Volume Batch: Systems Note: if the reaction occurs in the liquid phase or if a gas phase reaction occurs in a rigid (e. g. , steel) batch reactor Then

Example

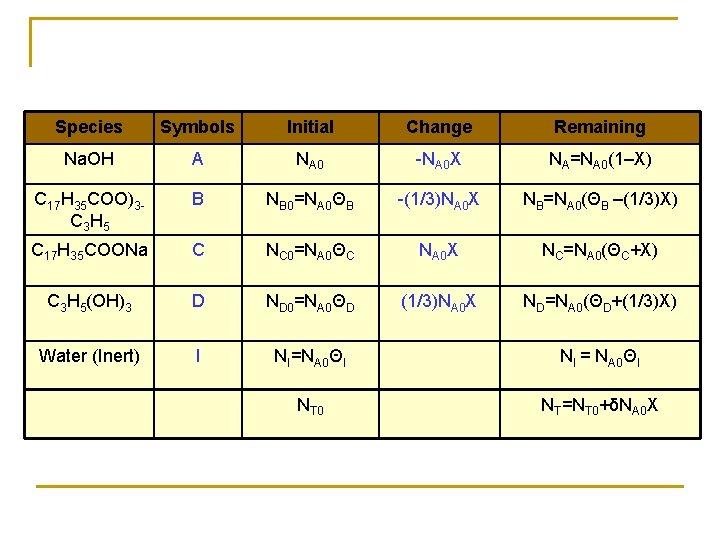
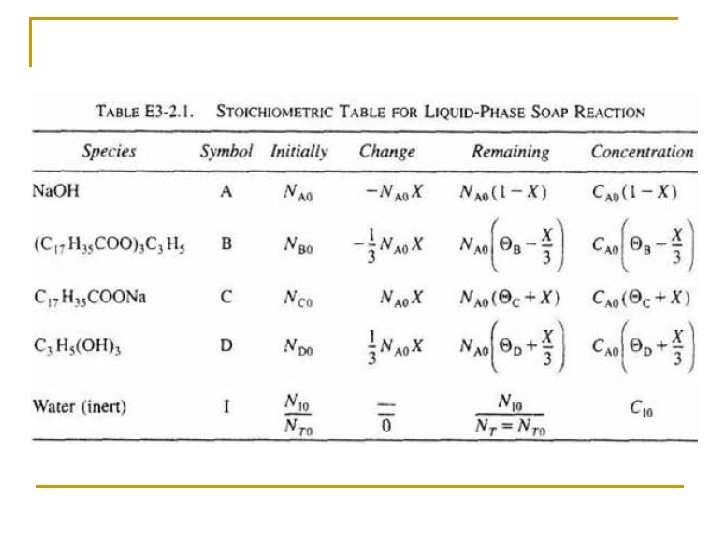
Species Symbols Initial Change Remaining Na. OH A NA 0 -NA 0 X NA=NA 0(1–X) C 17 H 35 COO)3 C 3 H 5 B NB 0=NA 0ΘB -(1/3)NA 0 X NB=NA 0(ΘB –(1/3)X) C 17 H 35 COONa C NC 0=NA 0ΘC NA 0 X NC=NA 0(ΘC+X) C 3 H 5(OH)3 D ND 0=NA 0ΘD (1/3)NA 0 X ND=NA 0(ΘD+(1/3)X) Water (Inert) I NI=NA 0ΘI NI = NA 0ΘI NT 0 NT=NT 0+δNA 0 X

Flow System Stoichiometric Table

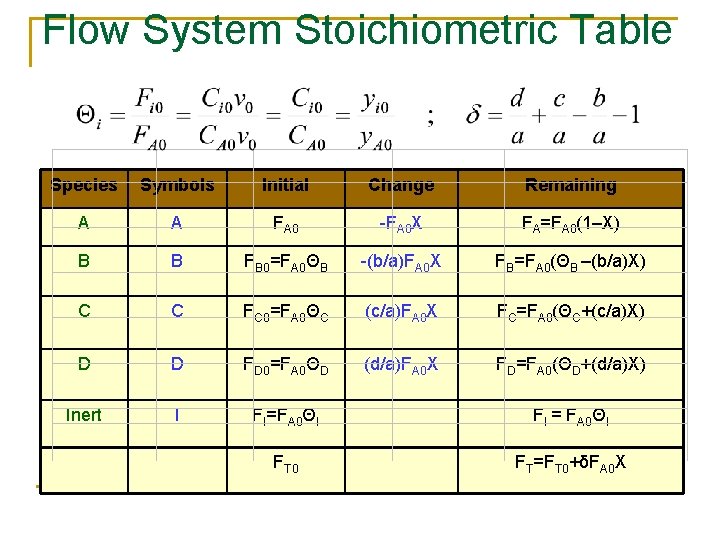
Flow System Stoichiometric Table Species Symbols Initial Change Remaining A A FA 0 -FA 0 X FA=FA 0(1–X) B B FB 0=FA 0ΘB -(b/a)FA 0 X FB=FA 0(ΘB –(b/a)X) C C FC 0=FA 0ΘC (c/a)FA 0 X FC=FA 0(ΘC+(c/a)X) D D FD 0=FA 0ΘD (d/a)FA 0 X FD=FA 0(ΘD+(d/a)X) Inert I FI=FA 0ΘI FI = FA 0ΘI FT 0 FT=FT 0+δFA 0 X

Concentration: Flow System Liquid Phase Flow System: This gives us -r. A = f(X) If the rate of reaction were: then we would have:

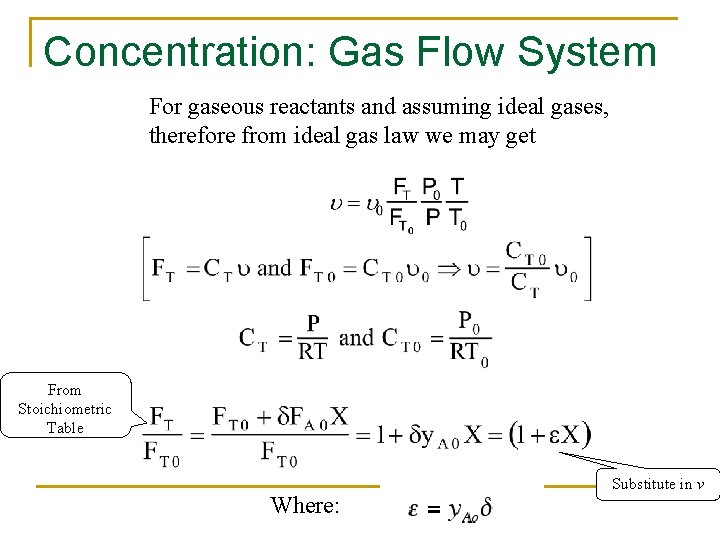
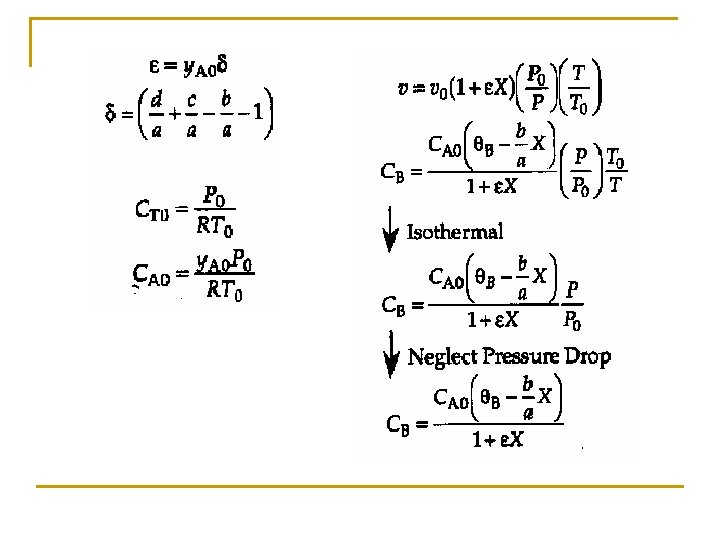
Concentration: Gas Flow System For gaseous reactants and assuming ideal gases, therefore from ideal gas law we may get From Stoichiometric Table Where: Substitute in v

Concentration: Gas Flow System Combining the compressibility factor equation of state with Z = Z 0 with and For example if the gas phase reaction has the rate law then k with

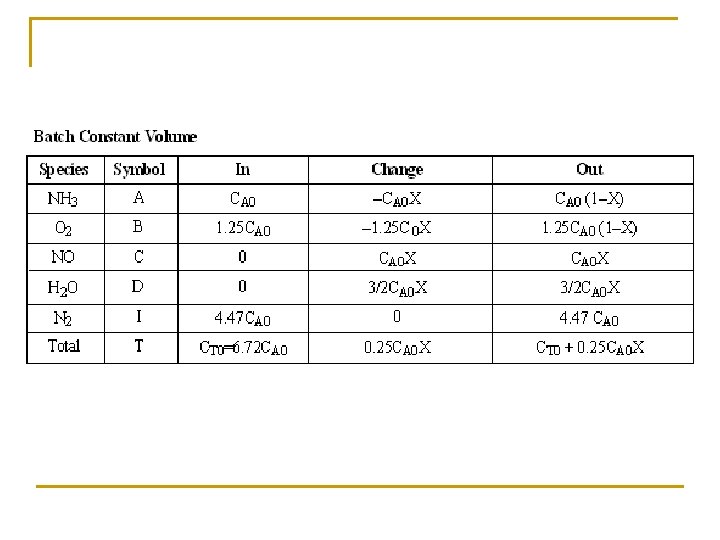
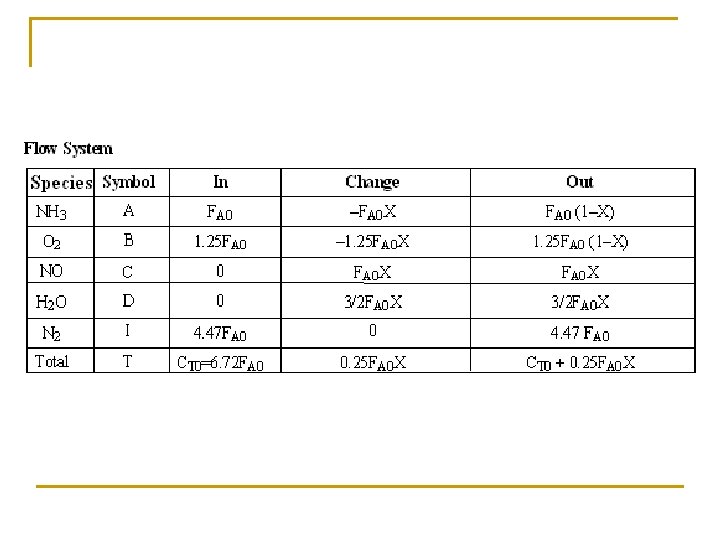
Example: Production of Nitric acid q Nitric acid is made commercially from nitric oxide. Nitric oxide is produced by the gas-phase oxidation of ammonia. 4 NH 3 + 5 O 2 4 NO + 6 H 2 O q The feed consists of 15 mol% ammonia in air at 8. 2 atm and 227°C.

(a) What is the total entering concentration? Assume ideal gas behavior.

(b) What is the entering concentration of ammonia?

(c) Set up a stoichiometric table with ammonia as your basis of calculation. Ø Express Ci for all species as functions of conversion for a constant-volume batch reactor. Ø Express PT as a function of X. Ø Express Pi and Ci for all species as functions of conversion for a flow reactor.

(d) Write the combined mole balance and rate law solely in terms of the molar flow rates and rate law parameters for C 1 and C 2 above. Assume the reaction is first order in both reactants

Tutorial 3

Kinetics of Homogeneous Reactions: reaction rate, stoichiometry, reaction order 1. A reaction has the stoichiometric equation A + B 2 R. What is the order of reaction? 2. Given the reaction: 2 NO 2 + 1/2 O 2 N 2 O 5 What is the relation between the rates of formation and disappearance of the three reaction components? 3. A reaction with stoichiometric equation: 1/2 A + B R + 1/2 S has the following rate expression : - r. A = k. CA 0. 5 CB What is the rate expression for this reaction if the stoichiometric equation is written as A + 2 B 2 R + S?

4. For the complex reaction with stoichiometry A + 3 B 2 R + S and with second-order rate expression: -r. A = k 1 CACB are the reaction rates related as follows: r. A = r. B = r. R? If the rates are not so related, then how are they related? Account for the sign, + or -. 5. A certain reaction has a rate given by: - r. A =0. 005 C 2 A mol/cm 3. min If the concentration is to be expressed in mol/l and time in hours, what would be the value and units of the rate constant?

Section A: Choose the correct answer from the following questions. 1. Which equation is used in arriving at the design equation for a batch reactor? A. Gj = Vrj B. d. Nj/dt = 0 C. Fjo = Fj = 0 D. E=mc 2

2. What assumptions are made when modeling an ideal tubular reactor? A. Steady sate and no radial variations B. Plug flow and liquid systems C. Gas flow and steady state D. That the reactor will photograph well A. Steady sate and no radial variations

3. What does the mole balance for a CSTR become if rj = - k. Cj? A. Cj = (Fjo-Fj)/V B. too complicated… C. V = (Fjo – Fj)/(k. Cj) D. V = (Fjo-Fj)/k

4. Which reactor is modeled by the equation V = (Fjo-Fj)/(k. Cj) if rj = -Cjk? A. CSTR B. The red one with polka dots C. Batch reactor D. Tubular reactor

5. What happens during a decomposition reaction? A. Species’ molecular configuration changes only B. A molecule rots C. Two molecules combine to give one molecule D. A molecule breaks down into smaller molecules

6. What assumption is made when studying an IDEAL CSTR? A. Innocent until proven guilty B. Adiabatic operation C. Perfect mixing D. Constant volume

7. What are the dimensions of k in the equation –ra = k Ca? A. moles 2/volume 2/time B. time/mole/volume C. three D. 1/time

8. What type of mathematical equation is used to express the rate law? A. Irreversible equation B. Differential equation C. Unsolvable equation D. Algebraic equation

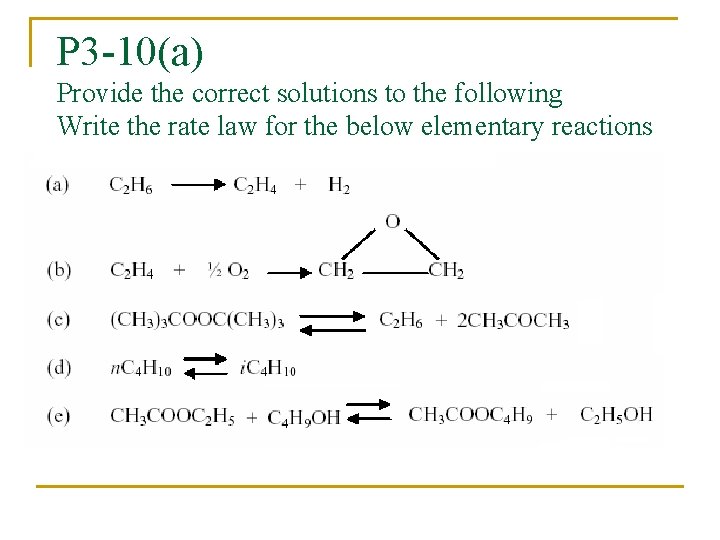
P 3 -10(a) Provide the correct solutions to the following Write the rate law for the below elementary reactions

P 3 -10(a)

P 3 -10(b)

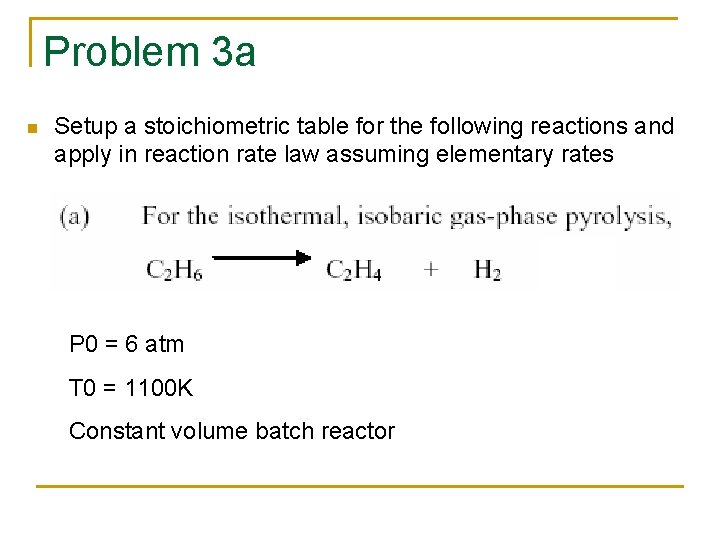
Problem 3 a n Setup a stoichiometric table for the following reactions and apply in reaction rate law assuming elementary rates P 0 = 6 atm T 0 = 1100 K Constant volume batch reactor

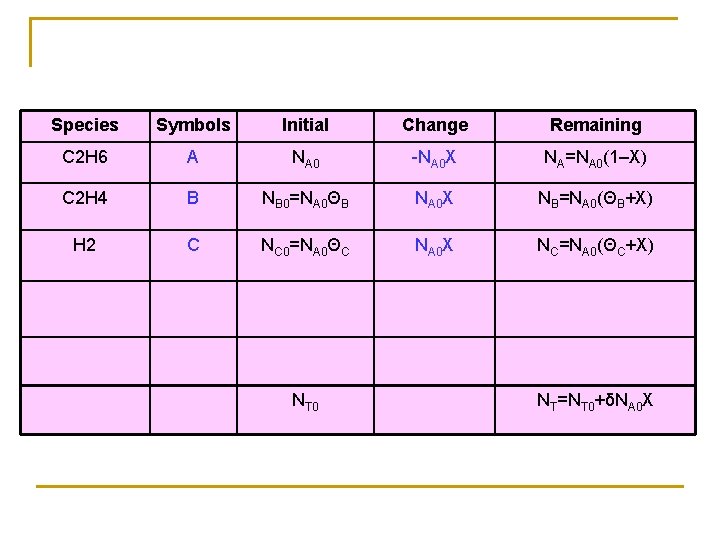
Species Symbols Initial Change Remaining C 2 H 6 A NA 0 -NA 0 X NA=NA 0(1–X) C 2 H 4 B NB 0=NA 0ΘB NA 0 X NB=NA 0(ΘB+X) H 2 C NC 0=NA 0ΘC NA 0 X NC=NA 0(ΘC+X) NT 0 NT=NT 0+δNA 0 X

Problem 3 b n Setup a stoichiometric table for the following reactions and apply in reaction rate law assuming elementary rates

Species Symbols Initial Change Remaining C 2 H 4 A FA 0 -FA 0 X FA=FA 0(1–X) O 2 B FB 0=FA 0ΘB - (b/a)FA 0 X FB=FA 0(ΘB-X) C 2 H 4 O C FC 0=FA 0ΘC=0 +FA 0 X FC=FA 0 X FT 0 FT=FT 0+δFA 0 X

Problem 4 The trimerization 3 A(g) A 3(g, l) is carried out isothermally and without pressure drop in a PFR at 298 K and 2 atm. As the concentration of A 3 increases down the reactor, A 3 begins to condense. The vapor pressure of A 3 at 298 K is 0. 5 atm. If an equal molar mixture of A and inert, I, is fed to the reactor, at what conversion of A will A 3 begin to condense?

Stoichiometric Table species Entering change leaving A FA 0 -FA 0 X I FA 0 - F A= FA 0(1 -X) FI=FA 0 A 3 - FA 0 X/3 F A= FA 0(1 -X) FI=FA 0 FA 3= FA 0 X/3 (y. A 3)(FT) FT = FA(2 -2 X/3)

P 3 -13 n n n The formation of nitoanalyne is formed from the reaction of ONCB and ammonia. The liquid phase reaction is 1 st order in both reactants with k=0. 0017 m 3/kmol. min at 188 C and activation energy = 11. 2 kcal/mol The concentrations of nitoanalyne and ONCB are 1. 8 and 6. 6 kmol/m 3 respectively.

P 3 -13 a Write the rate law of the disappearance of ONCB in terms of concentration?

P 3 -13 b Setup a stoiciometric table for flow system Species Entering Change Leaving A FA 0 -FA 0 X FA 0(1 -X) B FB 0=ΘBFA 0 -2 FA 0 X =(6. 6/1. 8)FA 0 FB= FA 0(ΘB-2 X) C 0 FA 0 X FC=FA 0 X D 0 FA 0 X FD=FA 0 X

P 3 -13(c)

P 3 -13(d)

P 3 -13(e)

P 3 -13(g)

Problem Q 4. P 4 -5 (CDROM) The liquid phase reaction A + B C follows an elementary rate law and is carried out isothermally in a flow system. The concentrations of the A and B feed streams are 2 M before mixing. The volumetric flow rate of each stream is 5 dm 3/min and the entering temperature is 300 K. The streams are mixed immediately before entering. Two reactors are available, a 200 dm 3 CSTR (that can be heated to 77°C or cooled to 0°C, and the other a PFR operated at 300 K. Note that k = 0. 07 dm 3/mol. min at 300 K and E = 20 kcal/mol. (a) What reactor and what conditions would you choose. Hint – first calculate the value of the constant k at 77°C (350 K). (b) How long would it take to achieve 90% conversion in a 200 dm 3 batch reactor with CAO = CBO = 1 M after mixing at a temperature of 77°C.

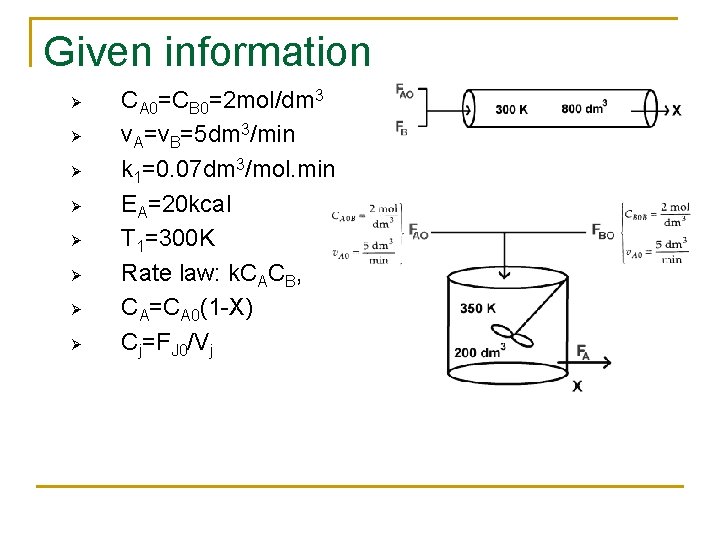
Given information Ø Ø Ø Ø CA 0=CB 0=2 mol/dm 3 v. A=v. B=5 dm 3/min k 1=0. 07 dm 3/mol. min EA=20 kcal T 1=300 K Rate law: k. CACB, CA=CA 0(1 -X) Cj=FJ 0/Vj

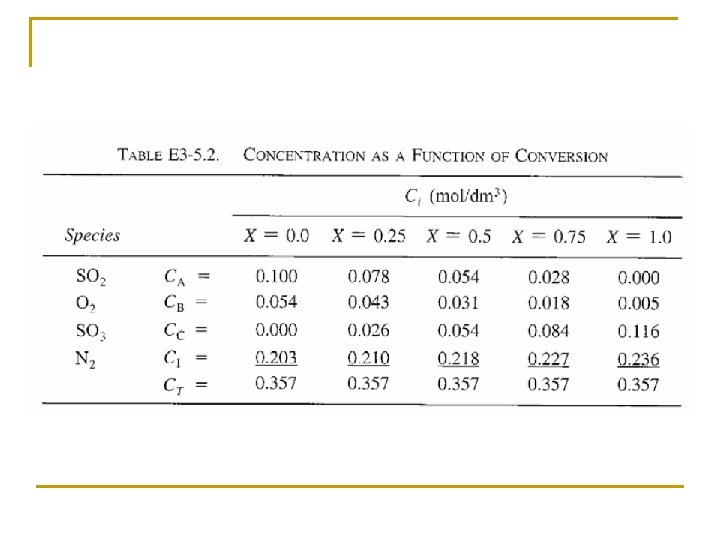
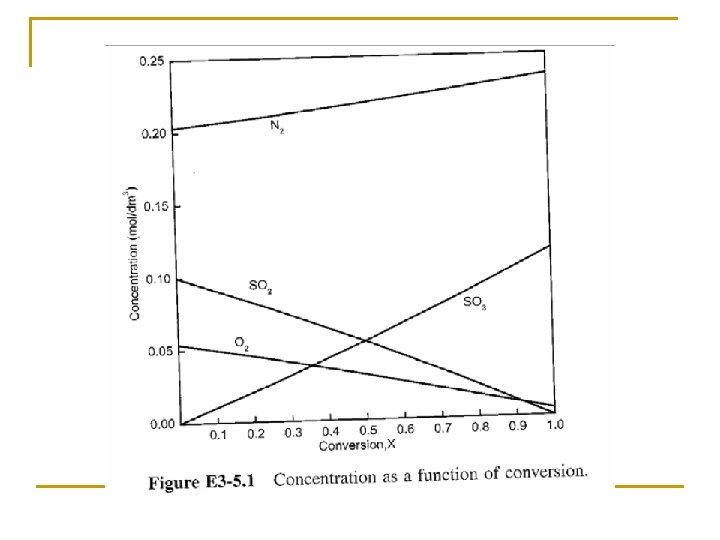
Problem 3. 2