Rate Conversion Outline Problem statement Standard approach Decimation

Rate Conversion

Outline Problem statement Standard approach Decimation by a factor D Interpolation by a factor I Sampling rate conversion by a rational factor I/D Sampling rate conversion by an arbitrary factor Orthogonal projection re-sampling General theory Spline spaces Oblique projection re-sampling General theory Spline spaces 2

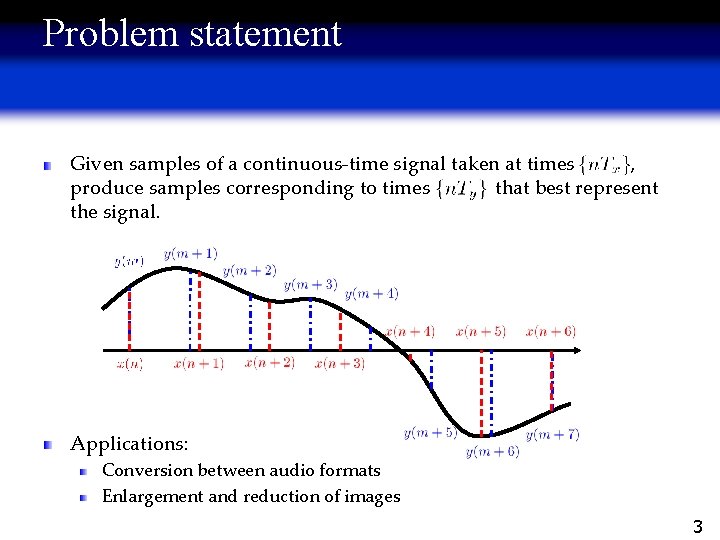
Problem statement Given samples of a continuous-time signal taken at times , produce samples corresponding to times that best represent the signal. Applications: Conversion between audio formats Enlargement and reduction of images 3

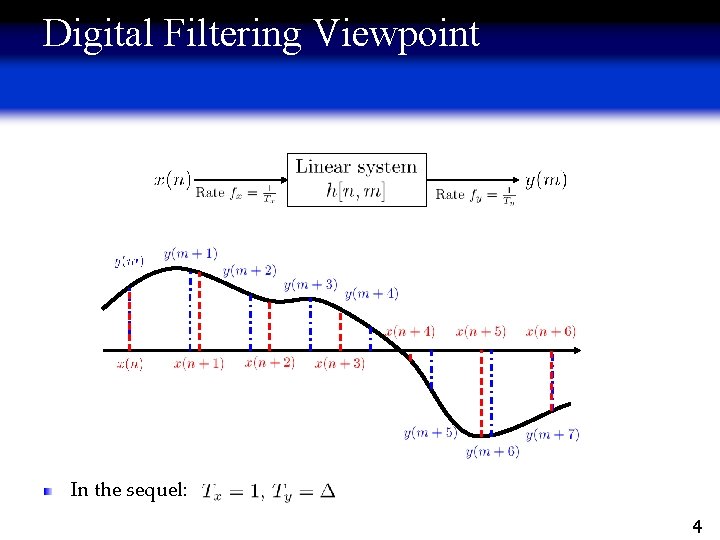
Digital Filtering Viewpoint In the sequel: 4

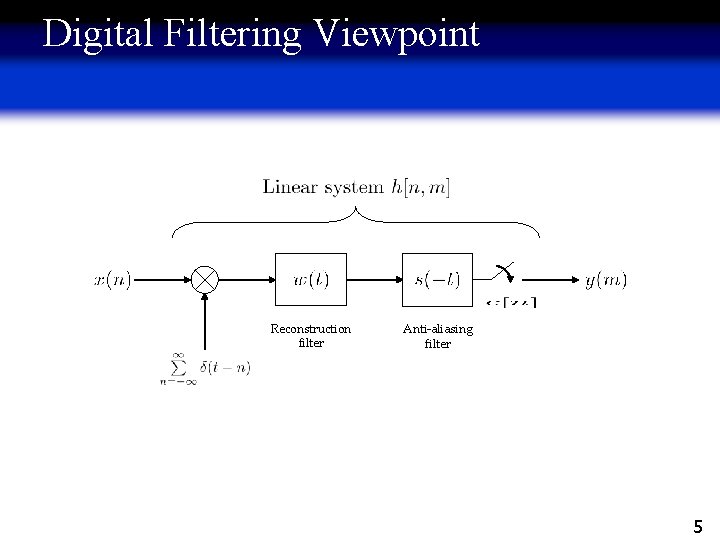
Digital Filtering Viewpoint Reconstruction filter Anti-aliasing filter 5

Standard Approach Decimation by a Factor D Standard choice (for avoiding aliasing): 6

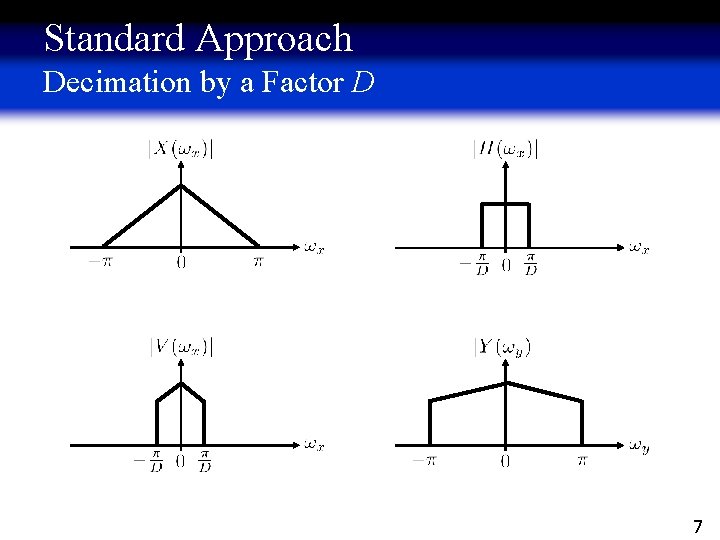
Standard Approach Decimation by a Factor D 7

Standard Approach Interpolation by a Factor I Standard choice (for suppressing replicas): 8

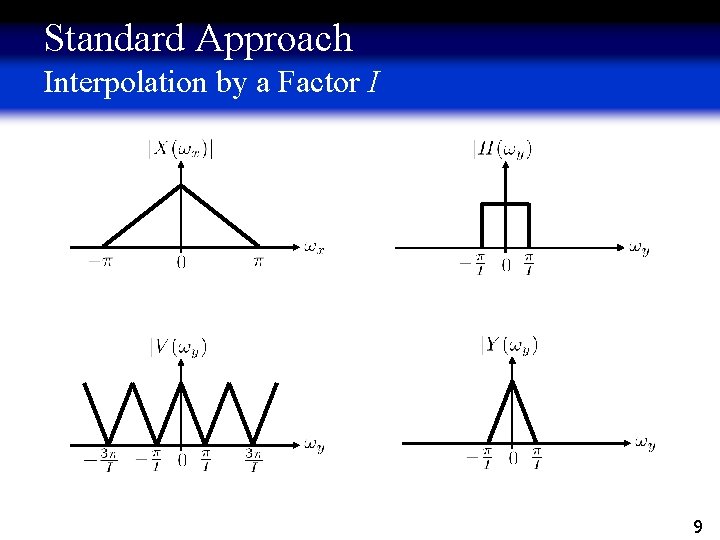
Standard Approach Interpolation by a Factor I 9

Standard Approach Conversion by a Rational Factor I/D If the factor is not rational then conventional rate conversion cannot be implemented using up-samplers, down-samplers and digital filters. To retain efficiency, it is custom to resort to non-exact methods such as first and second order approximation. 10

Orthogonal Projection Re-Sampling Reinterpretation of Standard Approach Reconstruction filter Anti-aliasing filter The prior and re-sampling spaces are related by a scaling of the generating function. 11

Orthogonal Projection Re-Sampling General Spaces 12

Orthogonal Projection Re-Sampling General Spaces 13

Orthogonal Projection Re-Sampling General Spaces 14

Orthogonal Projection Re-Sampling General Spaces 15

Orthogonal Projection Re-Sampling Summary Prefilter Rate conversion Postfilter For splines, there is a closed form for each of the components. 16

Orthogonal Projection Re-Sampling Splines Prefilter Postfilter 17

Orthogonal Projection Re-Sampling Examples 18

Orthogonal Projection Re-Sampling Splines 19

Orthogonal Projection Re-Sampling Interpretation Prefilter Reconstruction filter Anti-aliasing filter Postfilter Problem: The exact formula for the conversion block gets very hard to implement for splines of degree greater than 1. Solution: Use a simple anti-aliasing filter, which is not matched to the reconstruction space, and compensate by digital filtering. Thus, instead of orthogonally projecting the reconstructed signal onto the reconstruction space, we oblique-project it. 20

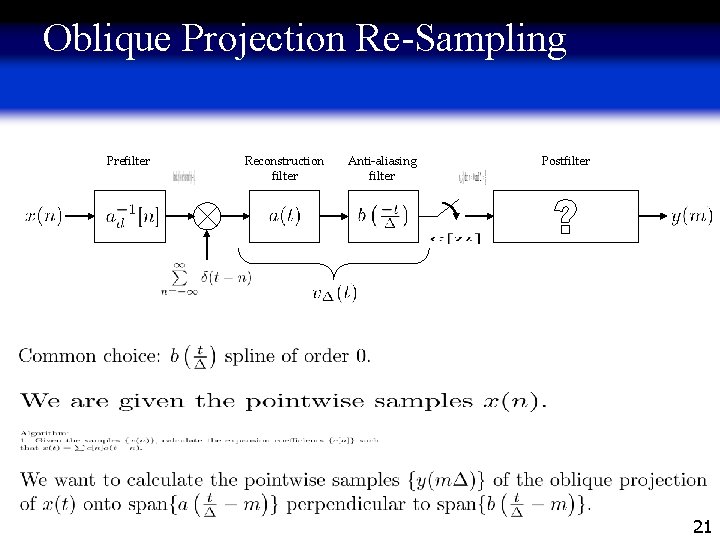
Oblique Projection Re-Sampling Prefilter Reconstruction filter Anti-aliasing filter Postfilter 21

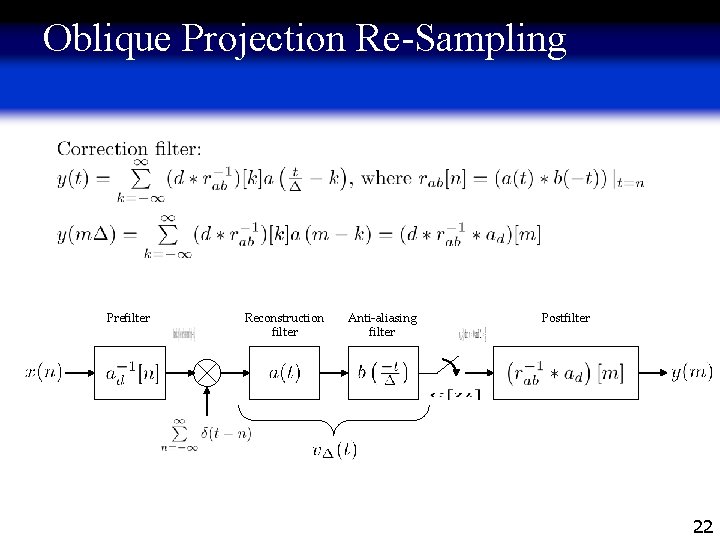
Oblique Projection Re-Sampling Prefilter Reconstruction filter Anti-aliasing filter Postfilter 22

Orthogonal Projection Re-Sampling Examples 23

Orthogonal Projection Re-Sampling Examples 24

Orthogonal Projection Re-Sampling Examples 25