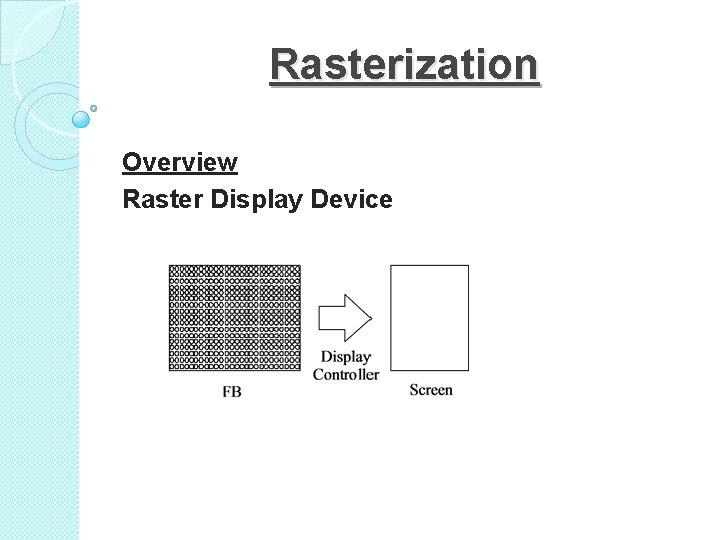
Rasterization Overview Raster Display Device Scan Conversion Rasterization






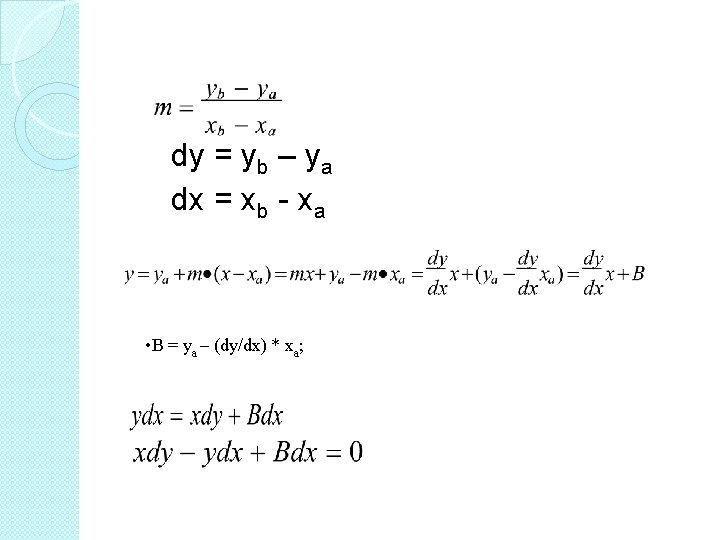



















![�Pattern Filling set. Pixel. Color(x, y, pattern[x%M, y%N]); The size of the pattern is �Pattern Filling set. Pixel. Color(x, y, pattern[x%M, y%N]); The size of the pattern is](https://slidetodoc.com/presentation_image_h/0cb1f107a2be23718f3f0806153fb199/image-39.jpg)






![• Ni [P(t)-PEi]=0 • Ni [P 0+t. D-PEi]=0 • Ni [P 0 -PEi] • Ni [P(t)-PEi]=0 • Ni [P 0+t. D-PEi]=0 • Ni [P 0 -PEi]](https://slidetodoc.com/presentation_image_h/0cb1f107a2be23718f3f0806153fb199/image-50.jpg)





- Slides: 55

Rasterization Overview Raster Display Device

Scan Conversion / Rasterization: converting vector graphics into raster graphics (determining pixels in raster graphics to represent primitives in vector graphics).

� Scan Converting Lines The Basic Incremental Algorithm A line scan-converting algorithm computes the coordinates of the pixels that lie on or near an ideal, infinitely thin straight line imposed on a 2 D grid. (Selects pixels on the line to light up. ) Pb(xb, yb) Pa(xa, ya)

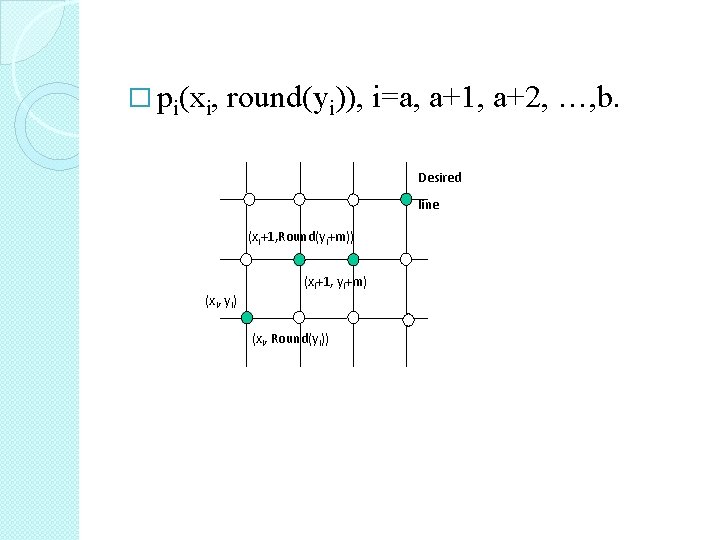
We need to compute xa, xa+1, xa+2, …, xb ya, ya+1, ya+2, …, yb dy=yb-ya; dx=xb-xa; m = dy /dx; Xi, for i = a, a+1, …, b.

�To increase efficiency, we consider yi = ya + m*(xi – xa) and xi+1= xi + 1 yi+1= ya + m*(xi+1 - xa) = ya + m*(xi – xa) + m = yi + m …. Since pixels are at integer locations, we need round up if m is not an integer:

� pi(xi, round(yi)), i=a, a+1, a+2, …, b. Desired line (xi+1, Round(yi+m)) (xi, yi) (xi+1, yi+m) (xi, Round(yi))

DDA (digital differential analyzer): void Line(int xa, int ya, int xb, int yb, int color) { int x; float dy, dx, y, m; dy=yb-ya; dx=xb-xa; m=dy/dx; y=ya; for(x=xa; x<=xb; x++) { // light the pixel near (x, y) with the color set. Pixel. Color(x, (int)(y+0. 5), color); y += m; } }

�This code is only good for |m|<=1. �Swap x and y when calling the function with |m|>1, and a flag is needed for displaying the swapped case. �Drawbacks: accumulating error, FP operation.

�Midpoint Line Algorithm Bresenhan Algorithm: Only use integer operation. No accumulation error. �Rule: if midpoint below the line, use upper pixel; if it is above use lower pixel.
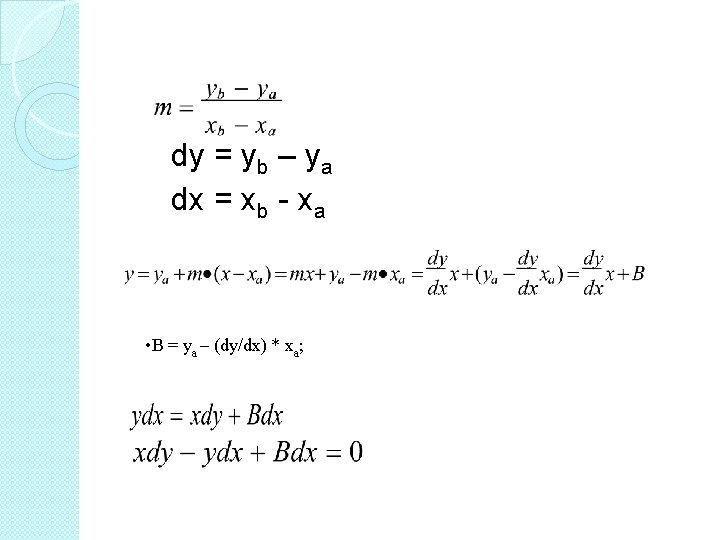
dy = yb – ya dx = xb - xa • B = ya – (dy/dx) * xa;

�Note b < 0 if dx > 0. �Decision variable for any given point P(xp, yp) is: d(xp, yp)=a xp + b yp + c. �if d=0: P is on the line �if d<0: P is above the line �if d>0: P is below the line

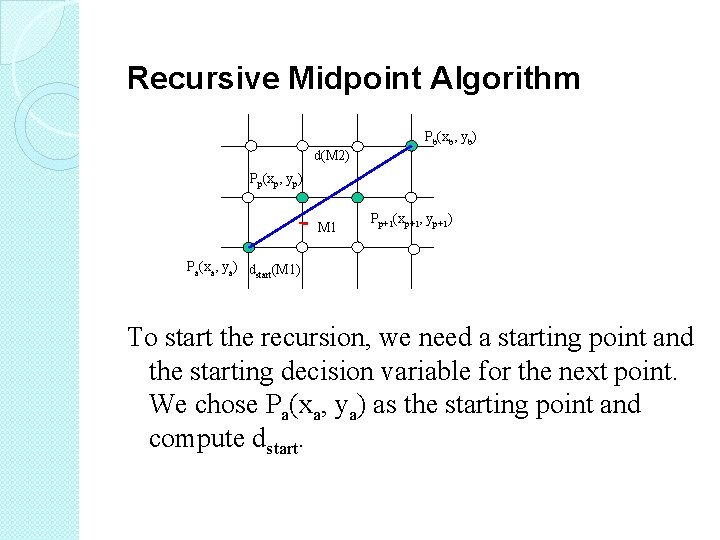
Recursive Midpoint Algorithm Pb(xb, yb) d(M 2) Pp(xp, yp) M 1 Pp+1(xp+1, yp+1) Pa(xa, ya) dstart(M 1) To start the recursion, we need a starting point and the starting decision variable for the next point. We chose Pa(xa, ya) as the starting point and compute dstart.

� Give any selected point P(xp, yp), we need decide where is the next point. � Compute the new decision variable for the midpoint. � if d=0: � if d<0: � if d>0: midpoint is on the line pick NE or E midpoint is above the line pick E midpoint is below the line pick NE

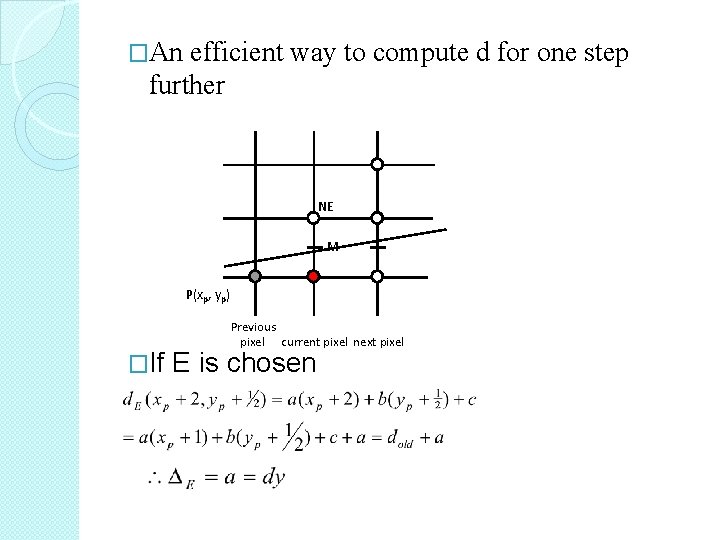
�An efficient way to compute d for one step further NE M P(xp, yp) �If Previous pixel current pixel next pixel E is chosen

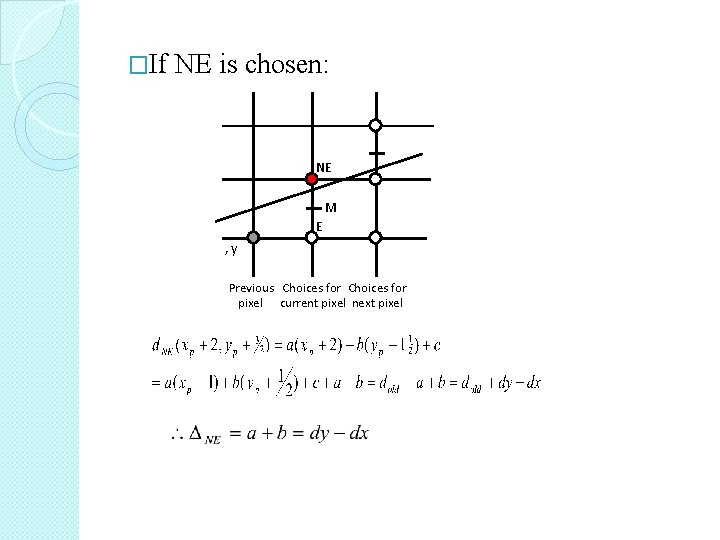
�If NE is chosen: NE M E , y Previous Choices for pixel current pixel next pixel

�To compute new d: To make integer operations, we use “ 2 d” instead of d. • Advantages of the Midpoint Algorithm: (1) Additions only. (2) Integer operations only.

void Midpoint. Line(int xa, int ya, int xb, int yb, int color) { int x, y; int dy, dx, incr. E, incr. NE, d; dx=xb-xa; dy=yb-ya; d=2*dy-dx; incr. E=2*dy; incr. NE=2*(dy-dx); x=xa; y=ya; Set. Pixel. Color(x, y, color);

while(x<xb) { if(d<=0) { x++; d+=incr. E; } else /* choose NE */ { x++; y++; d+=incr. NE; } Set. Pixel. Color(x, y, color); } } /* choose E */

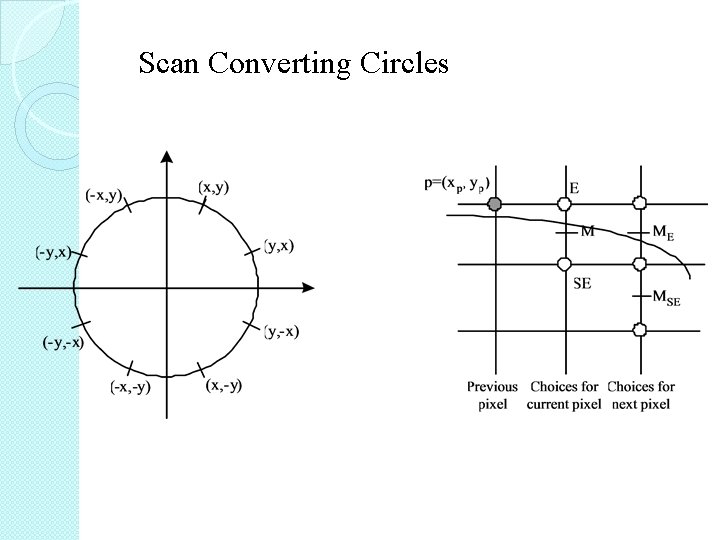
Scan Converting Circles

void Circle. Points(int x, int y, int color) { Set. Pixel. Color(x, y, color); Set. Pixel. Color(y, x, color); Set. Pixel. Color(y, -x, color); Set. Pixel. Color(x, -y, color); Set. Pixel. Color(-y, -x, color); Set. Pixel. Color(-y, x, color); Set. Pixel. Color(-x, y, color); }

� Center at origin, if it is not at origin, add shift value � Rule: midpoint inside circle, choose E, outside circle, choose SE. Given point P(x, y), the decision variable is d(x, y)=x 2+y 2 -R 2 � if d=0: midpoint is on the circle pick E or SE � if d<0: midpoint is inside the circle pick E � if d>0: midpoint is outside the circle pick SE ->At each step of the iteration: � Choose the pixel based on the sign of d, computed in previous iteration. � Update the decision variable d with corresponding .

� value for the next iteration: • dold<0 E • dold>0 SE

Initialization: P(xa=0, ya=R) on the circle d(xa, ya)=xa 2+ya 2 -R 2=0 void Midpoint. Circle(int R, int color) { int x, y, d; x=0; y=R; d=1 -R Circle. Point(x, y, color); while(y>x) { if(d<0) /* choose E */ { d+=2*x+3; x++; }

else { d+=(x-y)*2+5; x++; y--; } Circle. Point(x, y, color); } }

�Fill Rectangles -> Area Fill Ø Choosing pixels inside the area Ø set. Pixel. Color(x, y, color) We may need to compute color based on x, y if the filling is not a single color. A simple rectangle single color filling algorithm: int x, y for (y=ymin; y<=ymax; y++) /* for each scan line */ for (x=xmin; x<=xmax; x++) /* for each pixel */ set. Pixel. Color(x, y, color);

� Rules for shared edges =>A shared vertical edge belongs to the rightmost of the two sharing shapes =>A shared non-vertical edge belongs to the upper shape. =>Therefore only draw the pixels on the left and bottom edges. Revised code for rectangle single color filling: int x, y for (y=ymin; y<ymax; y++) for (x=xmin; x<xmax; x++) Set. Pixel. Color(x, y, color);

Fill Polygons (Polygon Scan-Conversion) • Parity: number of times a scan line has intersected the polygon. Initially it is 0 (even). • Extrema: the intersection points of the scan line with the polygon. • Span: a segment of a scan line between two consecutive extrema that is also within the polygon.

The Odd-Parity Rule =>For each intersection encountered, inverts the parity. =>Draw when the parity is odd. =>Don’t draw when it is even. The span-filling algorithm for filling a polygon on a scan-line: ->Find the intersections of the scan line with all edges of the polygon (extrema for the spans) ->Sort the intersections by increasing x coordinate ->Fill in all pixels between pairs of intersections that lie interior to the polygon (span), using the odd-parity rule to determine a point is inside the polygon or not. Polygon Filling Rule: draw only pixels that lie interior or on a left or bottom edge.

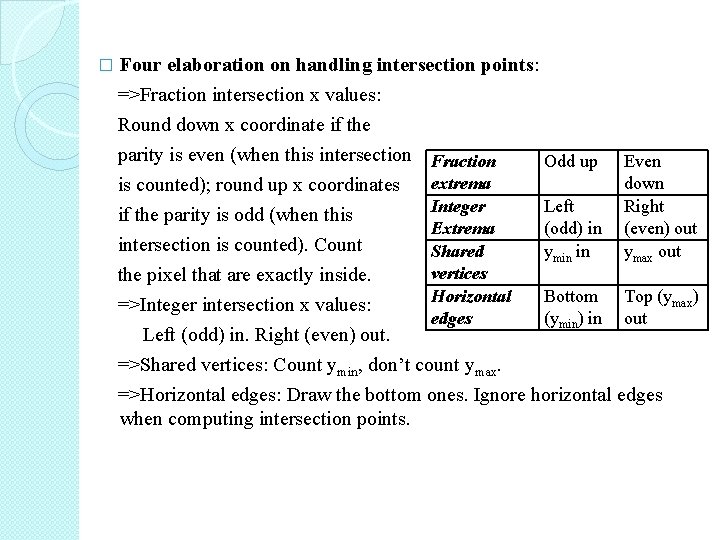
Four elaboration on handling intersection points: =>Fraction intersection x values: Round down x coordinate if the parity is even (when this intersection Fraction Odd up � Even down Right (even) out ymax out is counted); round up x coordinates extrema Integer Left if the parity is odd (when this Extrema (odd) in intersection is counted). Count Shared ymin in vertices the pixel that are exactly inside. Horizontal Bottom Top (ymax) =>Integer intersection x values: edges (ymin) in out Left (odd) in. Right (even) out. =>Shared vertices: Count ymin, don’t count ymax. =>Horizontal edges: Draw the bottom ones. Ignore horizontal edges when computing intersection points.

PSC (Polygon Scan Conversion): determine the pixels and set them to the specified color. =>Algorithm: Find the first and the last scan line � that intersect with the polygon. first: y=ymin: (min y value of the polygon) last: y=ymax: (max y value of the polygon) For each scan line between [ymin, ymax], fill the spans (span-filling) : Three stages of span filling: -> Find (the extrema by intersecting the scan line with the polygon). -> Sort (the extrema by x) -> Fill (the pixels using the odd-parity rule).

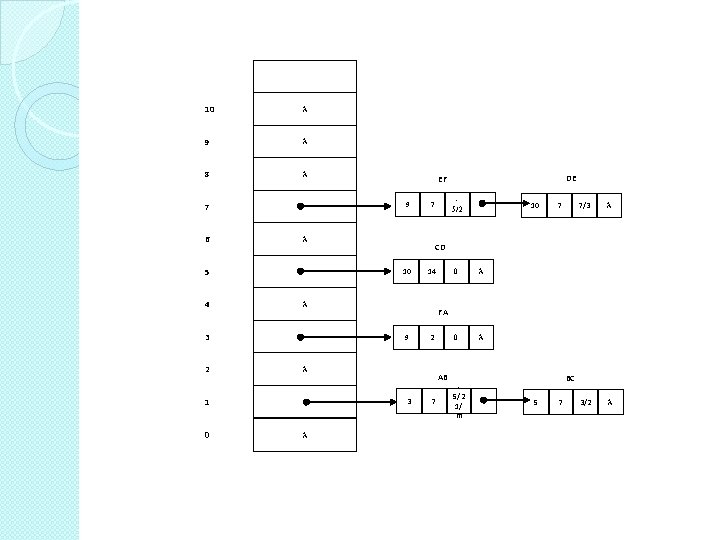
� Implementation � Edge Coherence: many edges intersected by scan line i also intersected by scan line i + 1. � AET: Active Edge Table, a linked list of extrema sorted by their x values for the current scan line. � ET: Edge Table (an array of pointers to the linked lists of newly intersected edges by each scan line).

10 9 8 9 7 6 4 0 14 2 AB 3 7 7/3 0 0 3/2 FA 9 1 10 CD 10 3 2 5/2 7 5 DE EF 7 5/2 1/ m BC 5 7

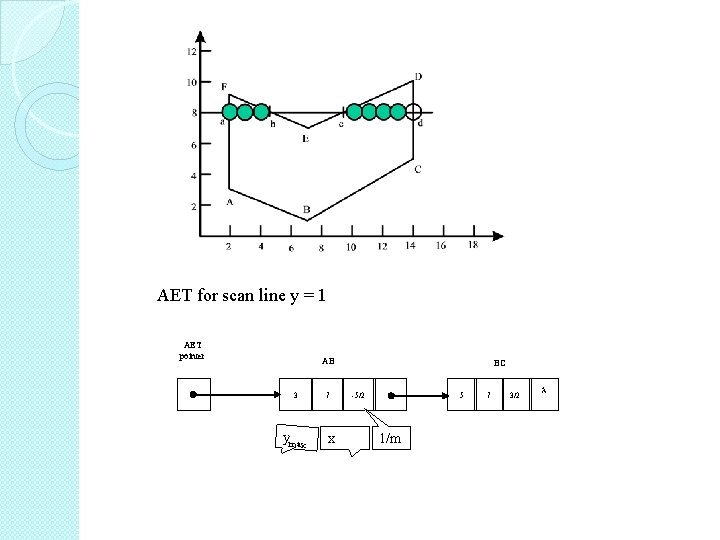
AET for scan line y = 1 AET pointer AB 3 ymax 7 x BC -5/2 5 1/m 7 3/2

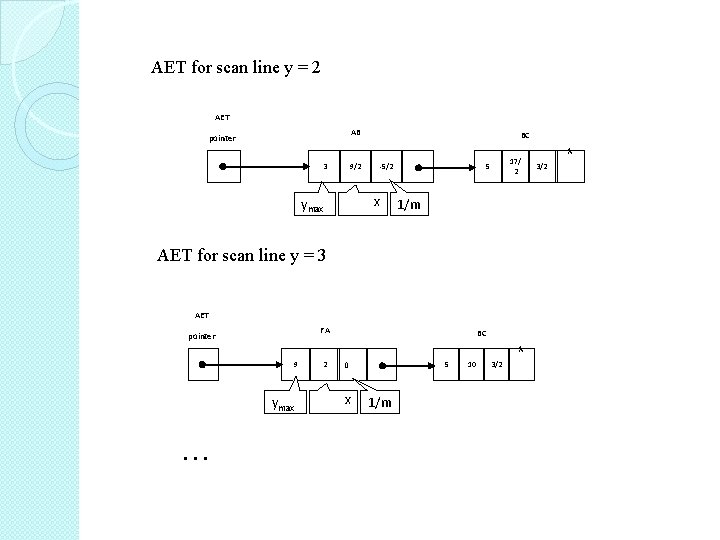
AET for scan line y = 2 AET AB pointer BC 3 9/2 -5/2 x ymax 17/ 2 5 1/m AET for scan line y = 3 AET FA pointer BC ymax … 2 5 0 x 9 1/m 10 3/2

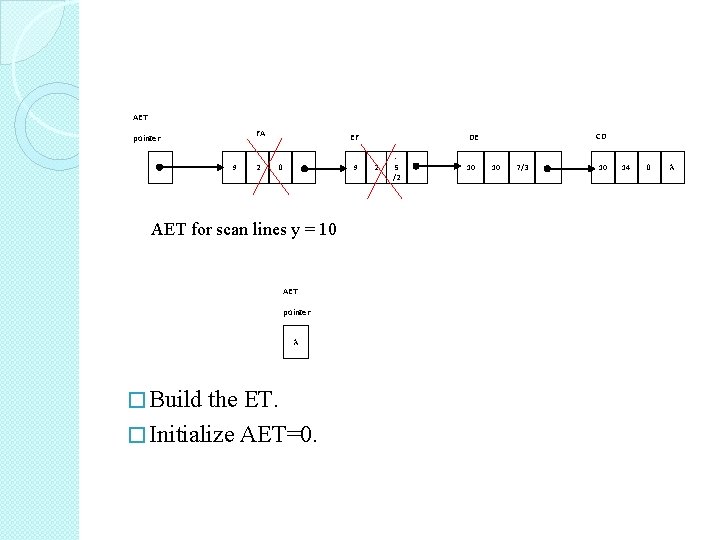
AET FA pointer 9 2 9 0 AET for scan lines y = 10 AET pointer � Build the ET. � Initialize AET=0. CD DE EF 2 5 /2 10 10 7/3 10 14 0

for (y= ymin; y<=ymax; y++) { ->Remove entries at AET whose ymax is smaller or equal to y. (ymax out). ->Add ET entry for this scan line into the AET. ->Compute the intersection point (extrema) x for each of the entries in the AET. ->Sort the entries by x. ->For each pair of extrema, fill the pixels in between. for (x=x 1; x<x 2; x++) Set. Pixel. Color(x, y); }

PSC (Polygon Scan Conversion) can be greatly simplified if the polygon is a triangle. � There is at most one pairs of extremes: one in and one out � There is at most one span of internal pixels � For smooth shading, we can interpolate the colors on the extremes using the colors on the three vertices, then interpolate colors on the internal pixels of the span based on the colors on the extremes. � All can be done by hardware. �

� Slivers: relax the filling rule, count nearby pixels Texture Filling
![Pattern Filling set Pixel Colorx y patternxM yN The size of the pattern is �Pattern Filling set. Pixel. Color(x, y, pattern[x%M, y%N]); The size of the pattern is](https://slidetodoc.com/presentation_image_h/0cb1f107a2be23718f3f0806153fb199/image-39.jpg)
�Pattern Filling set. Pixel. Color(x, y, pattern[x%M, y%N]); The size of the pattern is Mx. N. Determine the Texture Coordinates (s, t) for each vertex.

�ROP (Raster Operations) • Replace old pixel color with new color set. Pixel. Color(new. Color); • Mix pixel colors (Translucency) new. Color = α * new. Color + (1 -α) * old. Color; set. Pixel. Color(new. Color); • Four color channels: RGBA “A” is actually “α” for translucency.

�ROP: Logical Operations • Logic buffers (LB): same size as the FB. • To remember any logical values: e. g. , windows IDs. • Perform logical operations on the FB based on the logical values in the LB. e. g. , if(LB. ID == 8) set. Pixel. Color(Green);

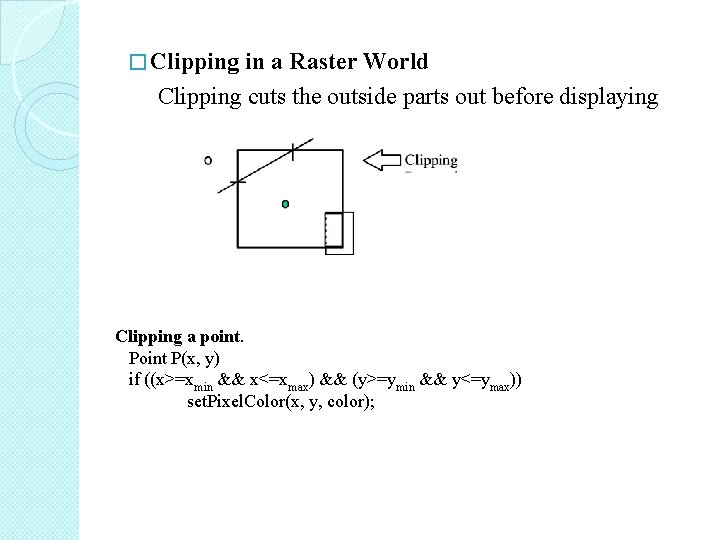
� Clipping in a Raster World Clipping cuts the outside parts out before displaying Clipping a point. Point P(x, y) if ((x>=xmin && x<=xmax) && (y>=ymin && y<=ymax)) set. Pixel. Color(x, y, color);

Clipping filled polygons =>Clip while scan-convert. =>Clip extrema in pairs: . Keep the pair if both extrema are inside. . Remove the pair if both extrema are outside and on the same side. . Move the outside extreme point to the edge if one extreme point is out and the other is in.

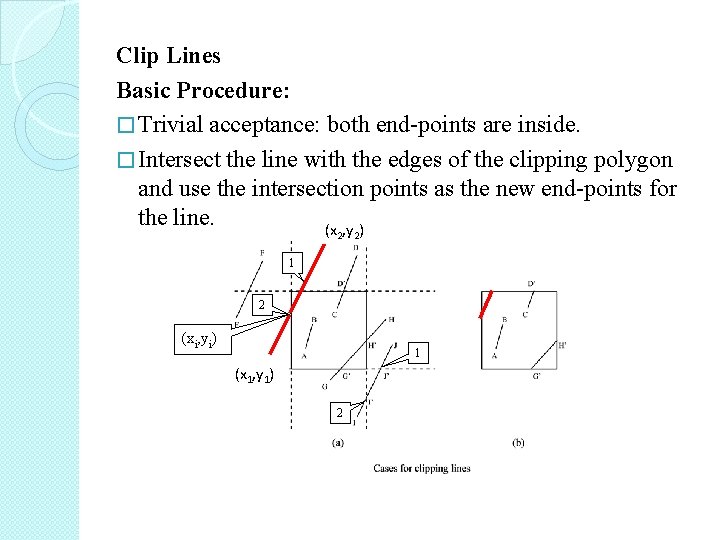
Clip Lines Basic Procedure: � Trivial acceptance: both end-points are inside. � Intersect the line with the edges of the clipping polygon and use the intersection points as the new end-points for the line. (x , y ) 2 2 1 2 (xi, yi) 1 (x 1, y 1) 2

How to find the intersection point of the line with an edge. e. g. left edge: x=xmin, ymin<=y<=ymax line equation intersection point: 1) xi=xmin 0<=t<=1 (xi, yi), ti 2) xi=x 1+ti(x 2 -x 1) 3) • For any line, we need to make sure: • 0<=ti<=1; • ymin<=yi<=ymax; xmin<=xi<=xmax • For vertical line: x 1=x 2, we need to make sure: xmin<=x 1<=xmax Four edge equations: left: x=xmin, ymin<=y<=ymax right: x=xmax, ymin<=y<=ymax top: y=ymax, xmin<=x<=xmax Bottom: y=ymin, xmin<=x<=xmax

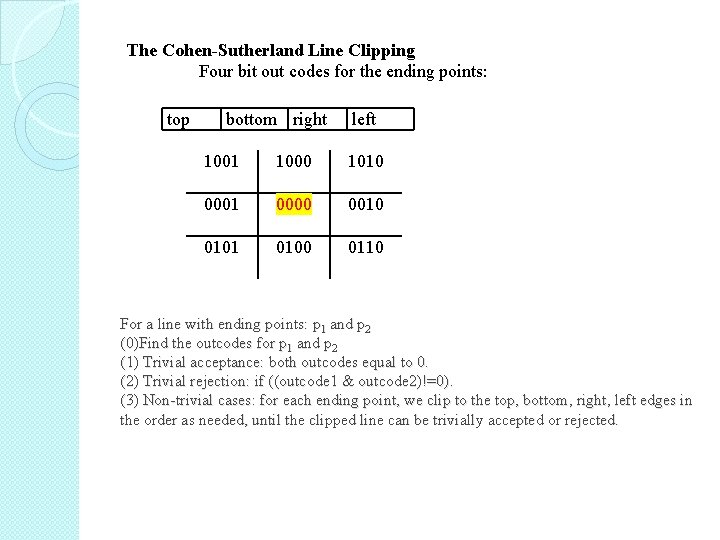
The Cohen-Sutherland Line Clipping Four bit out codes for the ending points: top bottom right left 1001 1000 1010 0001 0000 0010 0101 0100 0110 For a line with ending points: p 1 and p 2 (0)Find the outcodes for p 1 and p 2 (1) Trivial acceptance: both outcodes equal to 0. (2) Trivial rejection: if ((outcode 1 & outcode 2)!=0). (3) Non-trivial cases: for each ending point, we clip to the top, bottom, right, left edges in the order as needed, until the clipped line can be trivially accepted or rejected.

� Parametric Line-Clipping Algorithm � Cohen-Sutherland: computes x and y for every intersection points (including the intermediate ones). � Parametric: computes t first, only computes x and y for the clipped ending points. � Parametric Clipping Cyrus-Beck, Liang-Barsky � Basics: (1)Find intersection points between the line and the edges. Compute four t values (can be 0< or >1). (2)Determine which pair of t’s to use to define the line segment that is inside.

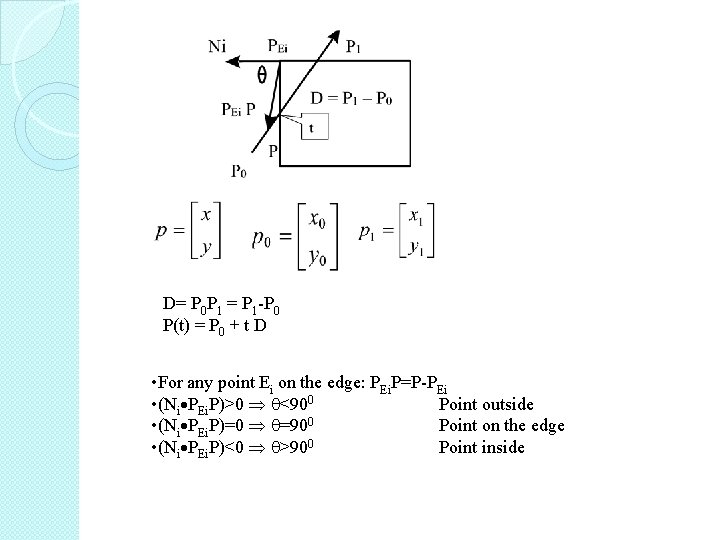
� Mathematics • V 1 V 2>0 <900 • V 1 V 2=0 =900 • V 1 V 2<0 >900 • The inside half-plane of an edge is the one containing the clipping rectangle • Counter clockwise rule: Enumerate the edges counter clockwise • inside half-plain is always to the left of a directed edge • The (outward) normal of an edge is pointing to the outside half-plane and perpendicular to the edge. (normal is an unit vector). • Computing t at an intersection point.

D= P 0 P 1 = P 1 -P 0 P(t) = P 0 + t D • For any point Ei on the edge: PEi. P=P-PEi • (Ni PEi. P)>0 <900 Point outside • (Ni PEi. P)=0 =900 Point on the edge • (Ni PEi. P)<0 >900 Point inside
![Ni PtPEi0 Ni P 0t DPEi0 Ni P 0 PEi • Ni [P(t)-PEi]=0 • Ni [P 0+t. D-PEi]=0 • Ni [P 0 -PEi]](https://slidetodoc.com/presentation_image_h/0cb1f107a2be23718f3f0806153fb199/image-50.jpg)
• Ni [P(t)-PEi]=0 • Ni [P 0+t. D-PEi]=0 • Ni [P 0 -PEi] + t Ni D = 0 • Taking care of Ni D=0 • The line is parallel to the edge. D is parallel to the edge • D=0 P 0=P 1

• Cyrus-Beck Parametric Line Clipping • Intersections are potentially entering the clipping rectangle(PE) if Ni D<0; >900. 2 PEs • Intersections are potentially leaving(PL) if Ni D>0; <900. 2 PLs • The inside line segment PE PL -> largest t. E, smallest t. L -> t. E<=t. L -> t. E>0; t. L<=1 • Special case: Ni D=0 -> Check x value for vertical line and y value for horizontal lines

Cyrus-Beck Algorithm { precalculate Ni and select a PEi (i=0, 1, 2, 3) for each edge for (each line to be clipped) { if(P 1==P 0) Point clip else { t. E=0; t. L=1 for (each edge) { if(Ni D==0) clip vertical / horizontal line else if(PE, Ni D<0) t. E=max(t. E, t) if(PL, Ni D>0) t. L=min(t. L, t) } } if(t. E > t. L) no display else display with t. E and t. L } } }

Polygon clipping (lines) Sutherland-Hodgeman Algorithm for(each edge of the clipping rectangle) { if the vertex is in the inside half plane add to the list else don’t add all intersection points with 0<= t <=1 } display list

Antiliasing • Aliasing: Jaggies or staircasing side effects in displaying graphics primitives • Antialiasing: Application of techniques that reduce or eliminate aliasing. • key: lines are of finite width

• Unweighted Area Sampling Intensity of a pixel is proportional to its area covered by the line (constant brightness within a pixel). • Weighted Area Sampling: • The intensity within a pixel is not constant. A small area closer to the pixel center has greater influence than does one at a greater distance.