Rasterising Polygons Anthony Steed 1999 2003 1 Overview

Overview What’s Inside a Polygon n Coherence n Active Edge Tables n Illumination Across

Naïve Filling Algorithm Find a point inside the polygon n Do a flood fill:

Critique n Horribly slow • But still very common in paint packages! n Stack

Recall Winding Number p 2 1 p 1 n-1 pn-1 n Works fine for

Another Implementation Shoot infinite ray from point n Count the number of intersections with

Counting Boundaries n If the shape is convex • Just count total number of

Intersections Concave Polygons n Draw a line from the test point to the outside

Point Coherency Ray shooting is fast, but note that for every point on one

Scan-Line Coherency n Intersection points of polygon edges with scan lines change little on

Overview of Active Edge Table For each scan-line in a polygon only certain edges

Setting Up n “fix” edges • make sure y 1<y 2 for each (x

Maintaining the AET n For each scan line • Remove all edges whose y

Drawing the AET Sort the active edges on x intersection n Pairs of edges

Setup n Edges are Edge Label a b c d n Edge Coordinates (1,

On Each Line Active Edge Table 0 empty 1 (7, 1, 0. 5), (4,

Gouraud Shading n Recall simple model for local diffuse reflection n Gouraud interpolates this

Gouraud Details n ET now contains • (y 2, x 1, dx, z 1,

Phong Shading Include specular component n Interpolate normals across the scan-line instead of colours

Recap n Active Edge Table Method • Implements a scan-line based fill method •

Slides: 21

Download presentation

Rasterising Polygons ©Anthony Steed 1999 -2003 1

Overview What’s Inside a Polygon n Coherence n Active Edge Tables n Illumination Across Polygons n 2

Naïve Filling Algorithm Find a point inside the polygon n Do a flood fill: n • Keep a stack of points to be tested • When the stack none empty – Pop the top point (Q) – Test if Q is inside or outside • If Inside, colour Q, push neighbours of Q if not already tested • It outside discard 3

Critique n Horribly slow • But still very common in paint packages! n Stack might be very deep n Need to exploit TWO types of coherency • Point coherency • Scan-line coherency 4

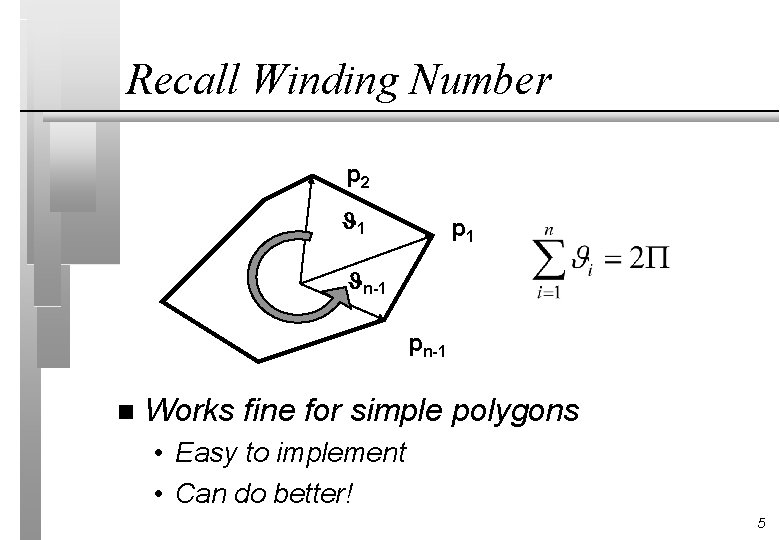
Recall Winding Number p 2 1 p 1 n-1 pn-1 n Works fine for simple polygons • Easy to implement • Can do better! 5

Another Implementation Shoot infinite ray from point n Count the number of intersections with the boundary n 6

Counting Boundaries n If the shape is convex • Just count total number of intersections: – 0 or 2 (outside) – 1 (inside) n Non-Zero Rule • Any number of intersections is possible, but if you just count the total you can not tell if you are inside or outside – Count +/-1 and use either the odd-even or nonzero rule 7

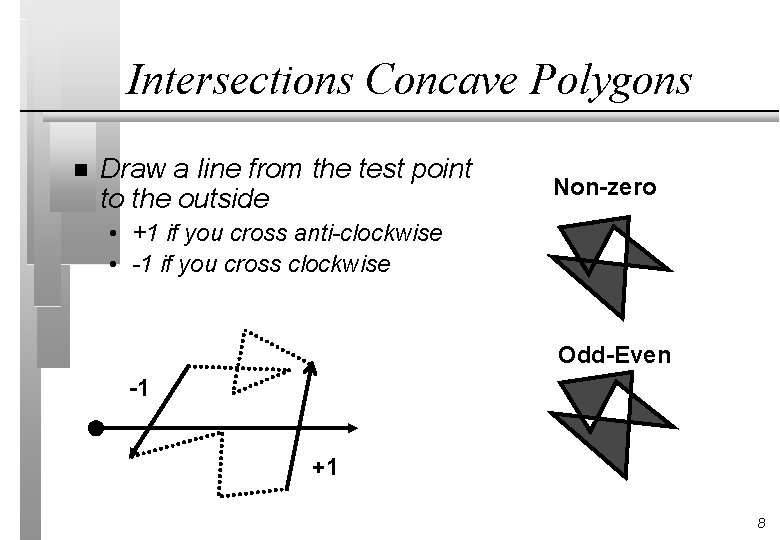
Intersections Concave Polygons n Draw a line from the test point to the outside Non-zero • +1 if you cross anti-clockwise • -1 if you cross clockwise Odd-Even -1 +1 8

Point Coherency Ray shooting is fast, but note that for every point on one scan line the intersection points are the same n Why not find the actual span for each line from the intersection points? n 9

Scan-Line Coherency n Intersection points of polygon edges with scan lines change little on a line by line basis xi-1 yi-1 xi yi 10

Overview of Active Edge Table For each scan-line in a polygon only certain edges need considering n Keep an ACTIVE edge table n • Update this edge table based upon the vertical extent of the edges n From the AET extract the required spans 11

Setting Up n “fix” edges • make sure y 1<y 2 for each (x 1, y 1) (x 2, y 2) n Form an ET • Bucket sort all edges on minimum y value • 1 bucket might contain several edges • Each edge element contains – (max Y, start X, X increment) 12

Maintaining the AET n For each scan line • Remove all edges whose y 2 is equal to current line • Update the x value for each remaining edge • Add all edges whose y 1 is equal to current line 13

Drawing the AET Sort the active edges on x intersection n Pairs of edges are the spans we require n n Caveats (discussed in the notes) • Don’t consider horizontal lines • Maximum vertices are not drawn • Plenty of special cases when polygons share edges 14

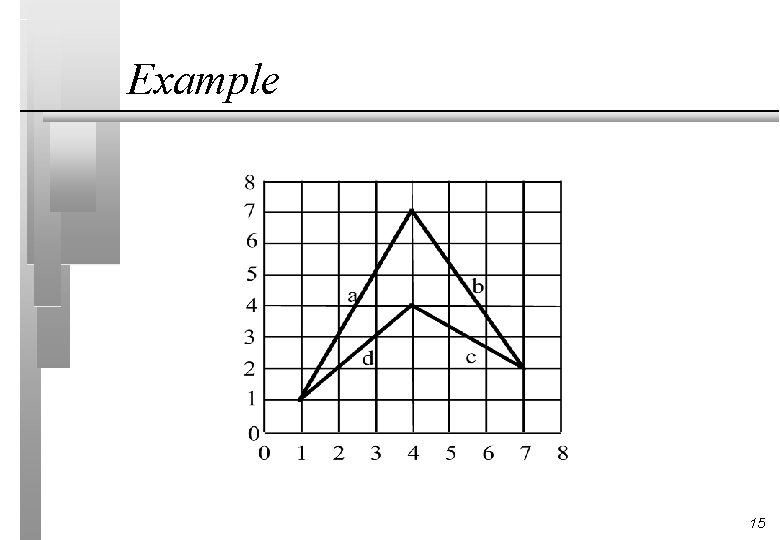
Example 15

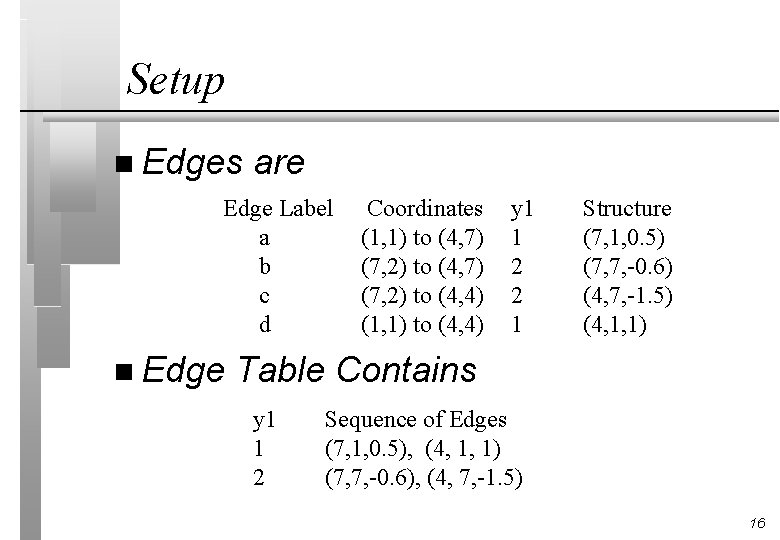
Setup n Edges are Edge Label a b c d n Edge Coordinates (1, 1) to (4, 7) (7, 2) to (4, 4) (1, 1) to (4, 4) y 1 1 2 2 1 Structure (7, 1, 0. 5) (7, 7, -0. 6) (4, 7, -1. 5) (4, 1, 1) Table Contains y 1 1 2 Sequence of Edges (7, 1, 0. 5), (4, 1, 1) (7, 7, -0. 6), (4, 7, -1. 5) 16

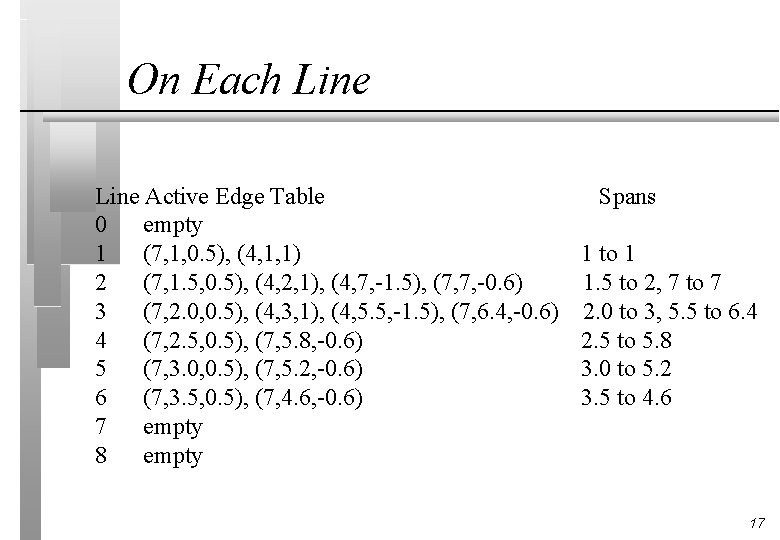
On Each Line Active Edge Table 0 empty 1 (7, 1, 0. 5), (4, 1, 1) 2 (7, 1. 5, 0. 5), (4, 2, 1), (4, 7, -1. 5), (7, 7, -0. 6) 3 (7, 2. 0, 0. 5), (4, 3, 1), (4, 5. 5, -1. 5), (7, 6. 4, -0. 6) 4 (7, 2. 5, 0. 5), (7, 5. 8, -0. 6) 5 (7, 3. 0, 0. 5), (7, 5. 2, -0. 6) 6 (7, 3. 5, 0. 5), (7, 4. 6, -0. 6) 7 empty 8 empty Spans 1 to 1 1. 5 to 2, 7 to 7 2. 0 to 3, 5. 5 to 6. 4 2. 5 to 5. 8 3. 0 to 5. 2 3. 5 to 4. 6 17

Gouraud Shading n Recall simple model for local diffuse reflection n Gouraud interpolates this colour down edges and across scan-lines in the same manner as we just did for depth 18

Gouraud Details n ET now contains • (y 2, x 1, dx, z 1, dz, r 1, dr, g 1, dg, b 1, db) – (we are running out of registers!) n Problems • not constant colour on rotation of points • misses specular highlights 19

Phong Shading Include specular component n Interpolate normals across the scan-line instead of colours n Recaptures highlights in the centre of polygons n 20

Recap n Active Edge Table Method • Implements a scan-line based fill method • Exploits point and scan-line coherency n Easily extended to support Gouraud and Phong shading • (Also visibility, shadows and texture mapping) 21