Rapid and Accurate Calculation of the Voigt Function

Rapid and Accurate Calculation of the Voigt Function D. Chris Benner Kendra L. Letchworth 9 th International HITRAN Conference June 26 -28, 2006

Why is this routine needed? • Spectra with higher signal to noise ratios require more accurate analysis routines. • Most fitting programs and simulations perform millions of calculations, so routines must also be fast. • Our routine calculates the Voigt profile to a relative accuracy of 10 -6. • 100 times more accurate than routines such as Drayson & Humlíček but requires 2 to 4 times less calculation time. • Our routine includes the imaginary part of the function for applications to line-mixing. • Option of returning the derivatives of the real Voigt profile with respect to x and y. They are calculated with relative accuracy of less than 10 -3, without significant additional calculation time required. • For more information about relative speed and accuracy of various Voigt routines (not including ours) see: F. Schreier, J. Q. S. R. T. , Vol. 48, 1992.

The Voigt Profile • • • v - v 0 : distance from line center αL : Lorentz half-width αD : Doppler half-width B. H. Armstrong, J. Q. S. R. T. , Vol. 7, 1966.

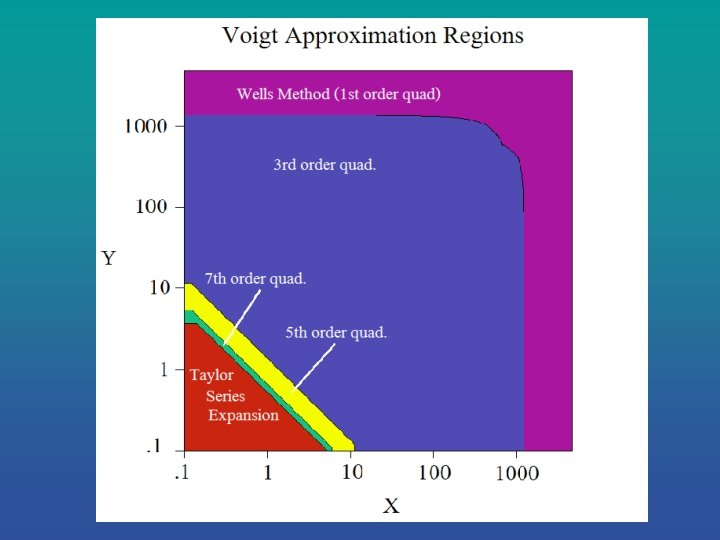
Mathematical Approximations: Gauss-Hermite Quadrature Points - vi Quadrature Weights - wi Real Part: Imaginary Part: Expression simplified using: • Symmetry: reduces the number of points calculated from n to (n+1)/2 by taking wi (f(vi) + f(-vi)) and simplifying expression. • Odd-order quadrature: a quadrature point always falls on v=0, giving the simple term at beginning of the equations. • Repeating expressions within equations: (y 2+x 2+vi 2) and (y 2+x 2+vi 2)2 -4 x 2 vi 2 can be calculated only once.

Mathematical Approximations: Taylor Series Expansion • 3 rd order Taylor expansion using a table of pre-computed values of the complex Voigt function (K+i. L) and its derivatives. Real Part: • ∂2 K/∂x 2=-∂2 K/∂y 2 decreases the number of stored derivatives of the real part (K) from 9 to 6. • Derivatives of the imaginary part (L) can be represented as functions of the derivatives of the real part since ∂L/∂x=-∂K/∂y and ∂L/∂y=∂K/∂x. Imaginary Part: • Δx=x-x 0, Δy=y-y 0 where (x 0, y 0) is the closest gridpoint. • A total of 8 values must be stored for each grid point (x 0, y 0) : K, L, ∂K/∂x, ∂K/∂y, ∂2 K/∂x 2, ∂3 K/∂x 3, ∂3 K/∂y 3.

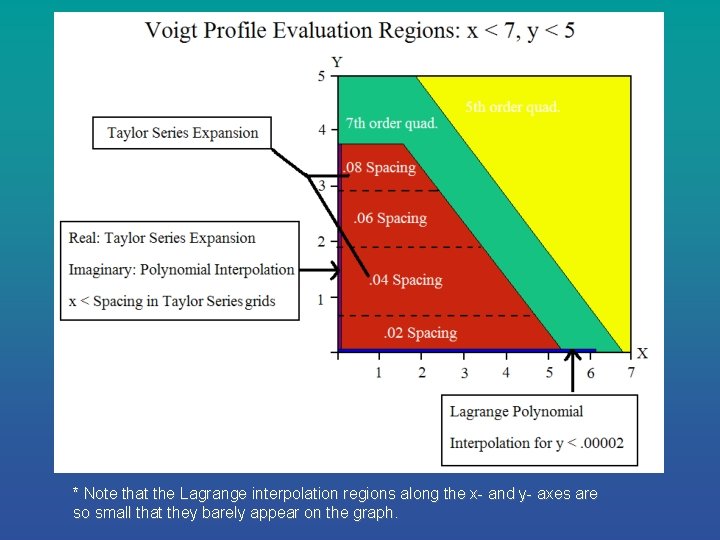
Mathematical Approximations: Lagrange Interpolating Polynomials • Used only in small areas when other methods fail, so does not contribute significantly to calculation time. • Employ equal grid point spacing dx and dy. • v 1, v 2, v 3 are three grid points and ∆v=(v- v 2)/dv • Four polynomial interpolations of P(v) below are required for a spline interpolation of real or imaginary part. • A total of eight evaluations is required for one complete function evaluation.

* Note that the Lagrange interpolation regions along the x- and y- axes are so small that they barely appear on the graph.

Programming Techniques • Calculates the Voigt profile for an entire spectral line at one time, removing unnecessary subroutine calls. • Each parameter involving y is calculated only once per spectral line, saving calculation time. • To do this we require equal spacing in wavenumber; a version of the routine called for individual points is available, but not as time efficient. • Interpolation tables stored as binary files on the hard drive and read in only when needed. • All files take up a total of 1. 5 MB of memory, a small price to pay for the increase in accuracy and speed.

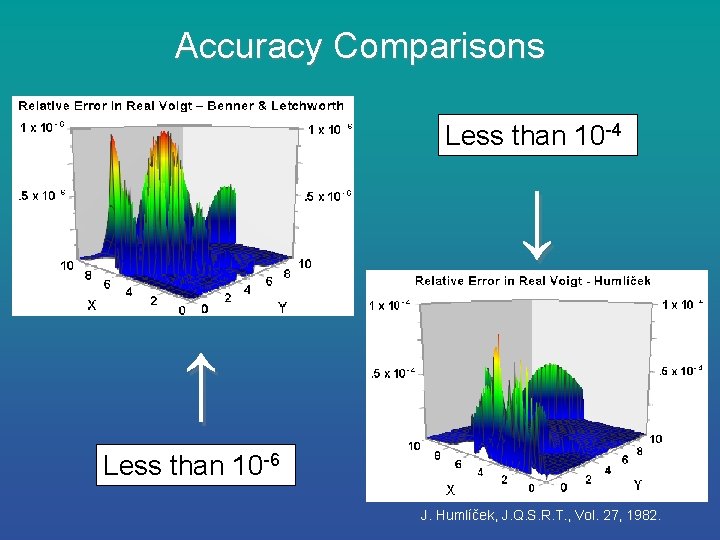
Accuracy Comparisons Less than 10 -4 ↓ ↑ Less than 10 -6 J. Humlíček, J. Q. S. R. T. , Vol. 27, 1982.

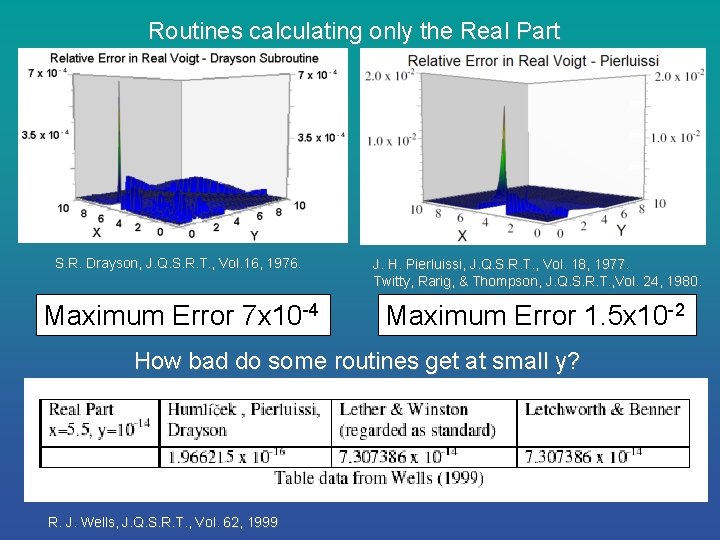
Routines calculating only the Real Part S. R. Drayson, J. Q. S. R. T. , Vol. 16, 1976. J. H. Pierluissi, J. Q. S. R. T. , Vol. 18, 1977. Twitty, Rarig, & Thompson, J. Q. S. R. T. , Vol. 24, 1980. Maximum Error 7 x 10 -4 Maximum Error 1. 5 x 10 -2 How bad do some routines get at small y? R. J. Wells, J. Q. S. R. T. , Vol. 62, 1999

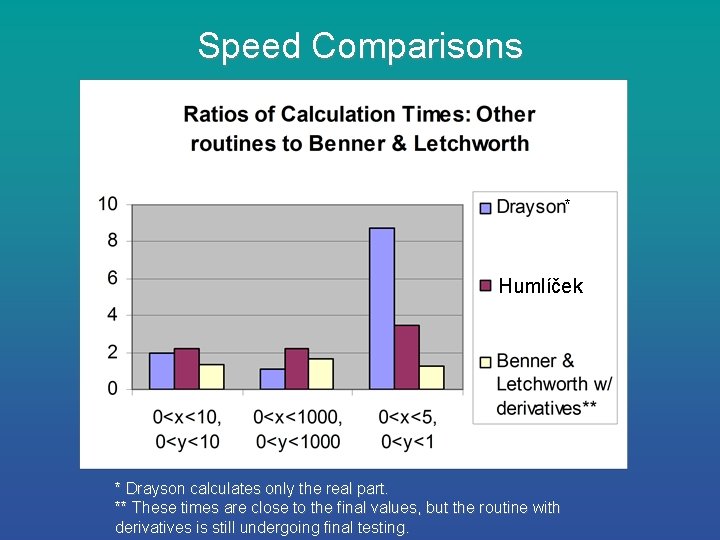
Speed Comparisons * Humlíček * Drayson calculates only the real part. ** These times are close to the final values, but the routine with derivatives is still undergoing final testing.