Rankine Cycle for Scientific Design of Power generation

Rankine Cycle for Scientific Design of Power generation System P M V Subbarao Professor Mechanical Engineering Department The policy of theoretically researching the PGS

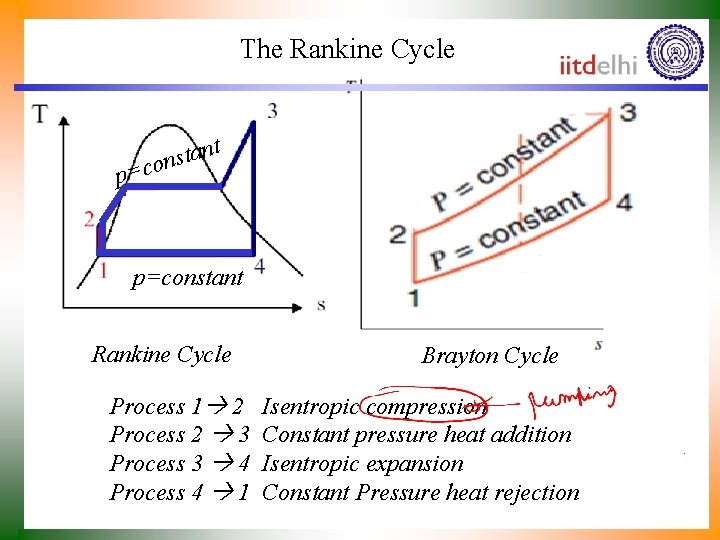
The Rankine Cycle t n a t s con p= p=constant Rankine Cycle Process 1 2 Process 2 3 Process 3 4 Process 4 1 Brayton Cycle Isentropic compression Constant pressure heat addition Isentropic expansion Constant Pressure heat rejection

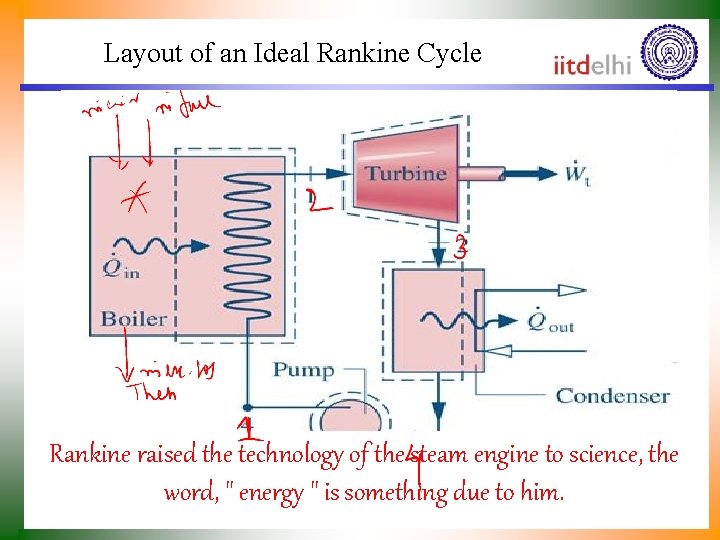
Layout of an Ideal Rankine Cycle Rankine raised the technology of the steam engine to science, the word, " energy " is something due to him.

Outlines of the Science of Energetics (1855) by William John Macquorn Rankine • Proceedings of the Royal Philosophical Society of Glasgow, Volume 3, by Royal Philosophical Society of Glasgow, 1855. pp. 121 -141. • The object of the present paper is, to present the principles, forming part of a science whose subjects are, material bodies and physical phenomena in a more systematic form. • It is proposed to call the SCIENCE OF ENERGETICS. • Definition of new terms: Substance, Property, Mass, Accident, Effort, or Active Accident, Passive Accident, Radical Accident, Effort as a Measure of Mass, Work. Energy, Actual and Potential. • Carnot theory is a special case of “Science of Energetics”

Laws of Nature for A Control Mass Conservation of Mass : First law of thermodynamics :

Rate Equations for Laws of Nature for A Control Mass Conservation of Mass : First law of thermodynamics :

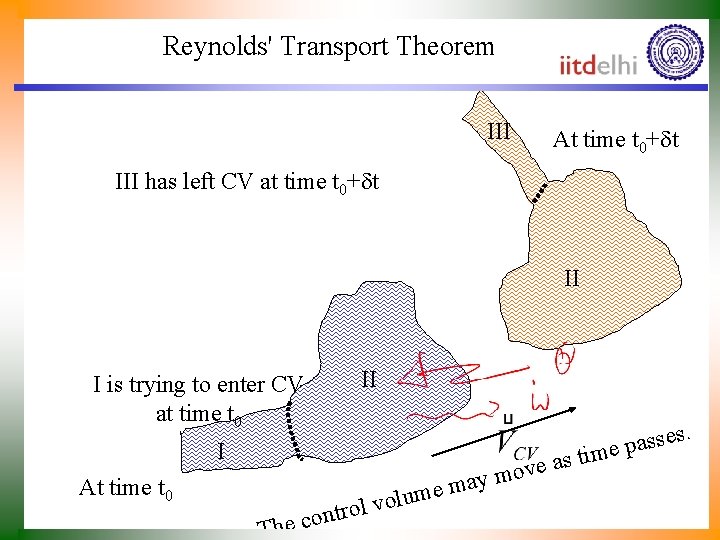
The Thermodynamic Control Volume • In real engineering devices, we are usually interested in a region of space, i. e, control volume and not particular control mass. • The laws of nature are connected to Control Mass. • Therefore, we need to transform Laws of Conservation for a control mass to a control volume. • This is accomplished through the use of Reynolds Transport Theorem. • Specially derived in thermodynamics for CV.

Reynolds' Transport Theorem III At time t 0+dt III has left CV at time t 0+dt II II I is trying to enter CV at time t 0 . s e s s a me p I ti s a e ov m y a em At time t 0 The c um l o v l ontro

Laws of Nature for A Control Volume • Conservation of mass: • First Law for A CV:

First Law for CV: Steady State Steady Flow Properties of CV are Invariant: • Conservation of mass: NO accumulation or depletion of mass of a CV. • Conservation of energy: No addition or removal of energy for a CV.

Rate of Work and Heat Transfers : SSSF Both rate of heat transfer and rate of work transfer are invariant. The work done per unit mass and heat transfer per unit mass are invariant. The specific work transfer at various parts of a CV can be different. The specific heat transfer at various parts of a CV can be different. Let :

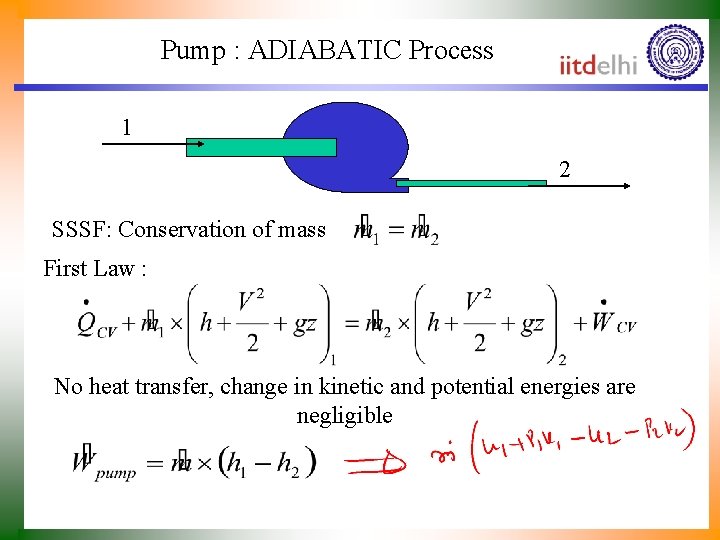
Pump : ADIABATIC Process 1 2 SSSF: Conservation of mass First Law : No heat transfer, change in kinetic and potential energies are negligible

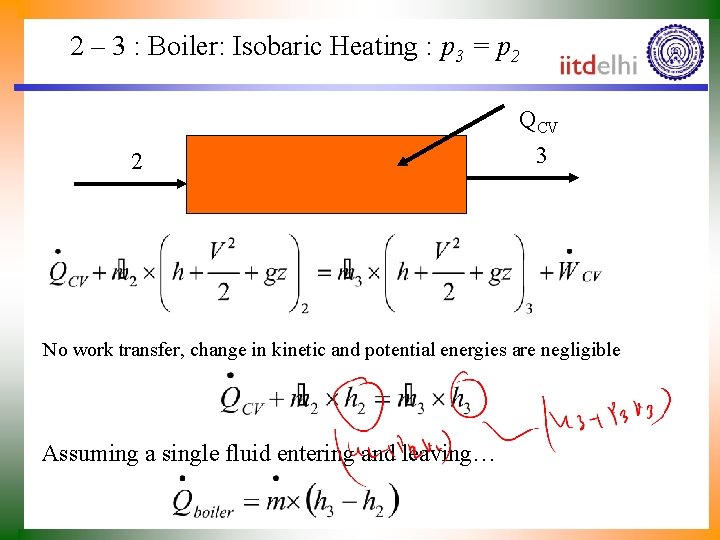
2 – 3 : Boiler: Isobaric Heating : p 3 = p 2 QCV 2 3 No work transfer, change in kinetic and potential energies are negligible Assuming a single fluid entering and leaving…

Turbine : Adiabatic Process : s 4=s 3 3 T 4 No heat transfer. Change in kinetic and potential energies are negligible Assuming a single fluid entering and leaving…

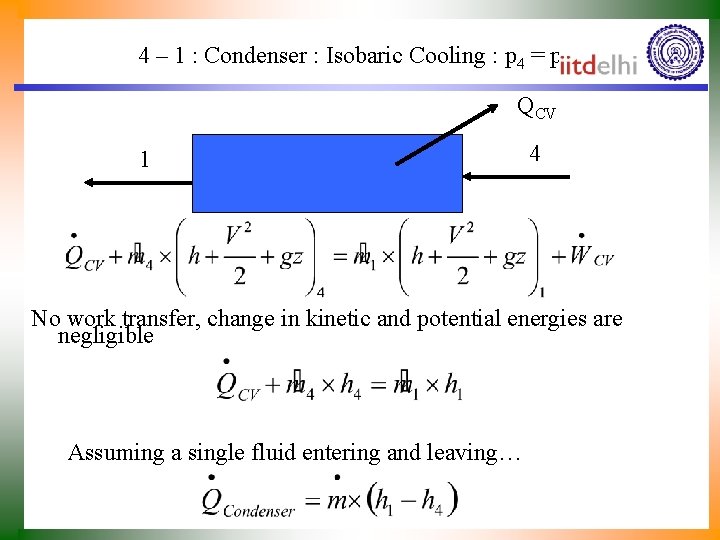
4 – 1 : Condenser : Isobaric Cooling : p 4 = p 1 QCV 1 4 No work transfer, change in kinetic and potential energies are negligible Assuming a single fluid entering and leaving…

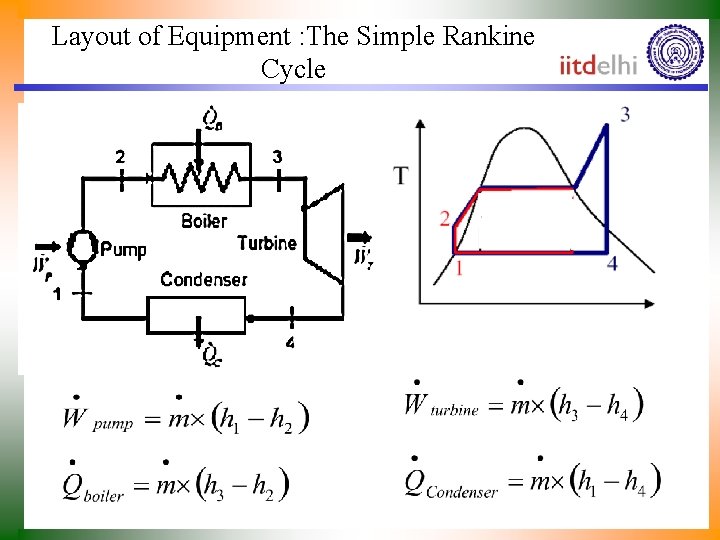
Layout of Equipment : The Simple Rankine Cycle

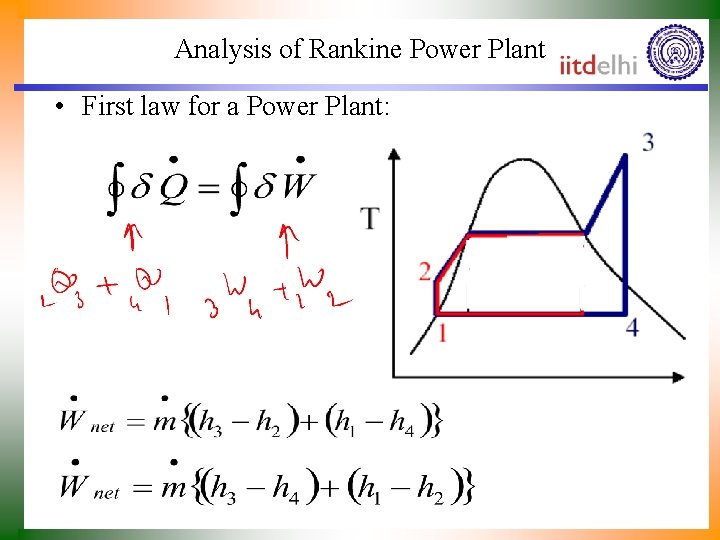
Analysis of Rankine Power Plant • First law for a Power Plant:

Cost to Benefit Ratio Analysis of Rankine Cycle

Cost to Benefit Ratio Analysis of Rankine Cycle

Heat Rate: An International Standard • The term “heat rate” simply refers to energy conversion efficiency, in terms of • “how much energy must be expended in order to obtain a unit of useful work. ” • In a combustion power plant, the fuel is the energy source, and the useful work is the electrical power supplied to the grid. • Because “useful work” is typically defined as the electricity, engineers tend to work with the net plant heat rate (NPHR). • Units: k. J/k. W-hr or k. Cal /k. W-hr

Method of Calculation • Net Plant power output : Pnet in k. W • Fuel consumption rate: mfuel kg/hr • Higher heating value or higher calorific value: HHV in k. J/kg Generation of most useful steam is first step in enhancing Pnet. Economics of Steam generation plays an importance….