Rank and Select data structures A basic problem

Rank and Select data structures

A basic problem ! D Abaco$Battle$Car$Cold$Cod. . Array of n string pointers to strings of total length m • (n log m) bits = 32 n bits. • it depends on the number of strings • it is independent of string length D Abaco Battle Car Cold Cod. . B 100000 1000 100. . Spaces are introduced for simplicity You could drop the $ How do you retrieve the k-th string?

Rank/Select Wish to index the bit vector B[1, m] (possibly compressed). Select 1(3) = 8 B 001010101011111110000011010101. . Rank 1(6) = 2 • Rankb(i) = number of b in B[1, i] m = |B| n = #1 • Selectb(i) = position of the i-th b in B Two approaches: (1) Takes |B| + o(|B|) bits of space, (2) Aims at achieving n log(m/n) bits, by deplyoing Elias-Fano + point (1)

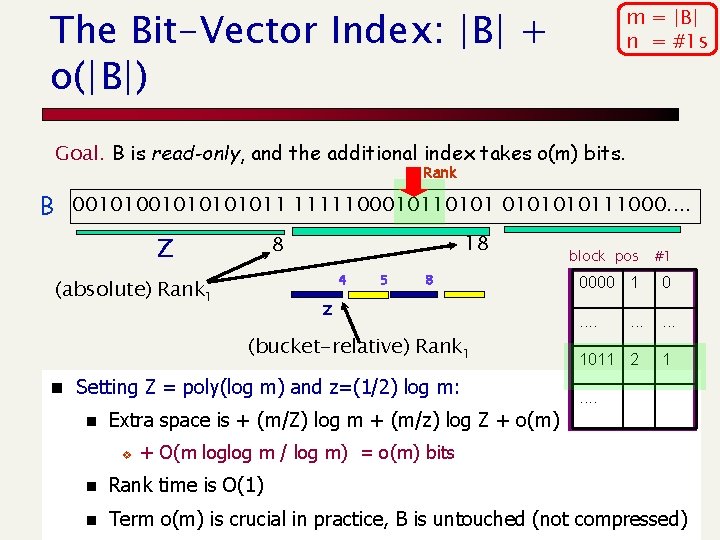
The Bit-Vector Index: |B| + o(|B|) m = |B| n = #1 s Goal. B is read-only, and the additional index takes o(m) bits. Rank B 001010101011 111110001011010111000. . 18 8 Z 4 (absolute) Rank 1 5 8 z (bucket-relative) Rank 1 n Setting Z = poly(log m) and z=(1/2) log m: n block pos #1 0000 1 0 . . 1011 2 1 . . Extra space is + (m/Z) log m + (m/z) log Z + o(m) v + O(m loglog m / log m) = o(m) bits n Rank time is O(1) n Term o(m) is crucial in practice, B is untouched (not compressed)

The Select operation m = |B| n = #1 s B 00101010101111111000001101010111001. . size r is variable until the subarray includes k = (log m)2 1 s n Sparse case: If r > k 2 = (log m)4 , we store explicitly the position of the k = (log m)2 1 s, because we have at most (m/r) blocks of this type, each taking (m/r) * k * log m bits = O(m / log m) = o(m) bits n Dense case: k ≤ r ≤ k 2, recurse by repeating the argument now with k’ = (log m)2. If r’ including k’ 1 s > log m bits, then store the k’ positions explicitly using O(log m) bits each, thus O(m/log m) = o(m) bits in total. Otherwise r’ < log m, and thus a precomputed table is enough. n Extra space is + o(m), and B is not touched! n Select time is O(1)

Via Elias-Fano (|L| + |H| + o(|H|)) Therefore B is not needed Recall that by setting w = log (m/n) and z = log n, where m = |B| and n = #1 then - Space = n log (m/n) bits + 2 n bits z = 3, w=2 0 1 2 3 4 5 6 7 (Build Select 1 on H so we need extra |H| + o(|H|) bits = 2 n + o(n) bits ) Select 1(i) on B uses L and (Select 1(H, i) – i) in +o(n) space Rank 1(i) on B Needs binary search over B

If you wish to play with Rank and Select m/10 + n log (m/n) Rank in 0. 4 msec, Select in < 1 msec vs 32 n bits of explicit pointers