Randomness Extractors applications and constructions Avi Wigderson IAS

Randomness Extractors: applications and constructions Avi Wigderson IAS, Princeton

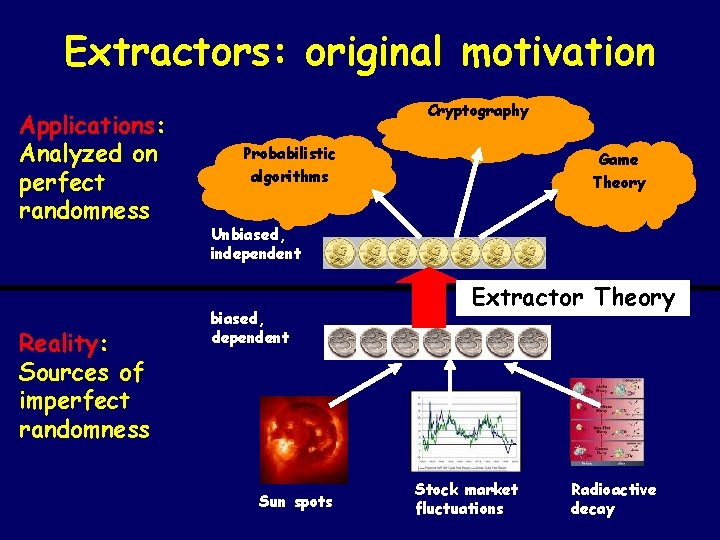
Extractors: original motivation Applications: Analyzed on perfect randomness Reality: Sources of imperfect randomness Cryptography Probabilistic algorithms Game Theory Unbiased, independent biased, dependent Sun spots Extractor Theory Stock market fluctuations Radioactive decay

Applications of Extractors • Using weak random sources in prob algorithms [B 84, SV 84, V 85, VV 85, CG 85, V 87, CW 89, Z 90 -91] • Randomness-efficient error reduction of prob algorithms [Sip 88, GZ 97, MV 99, STV 99] • Derandomization of space-bounded algorithms [NZ 93, INW 94, RR 99, GW 02] • • Distributed Algorithms [WZ 95, Zuc 97, RZ 98, Ind 02]. Hardness of Approximation [Zuc 93, Uma 99, MU 01] Cryptography [CDHKS 00, MW 00, Lu 02 Vad 03] Data Structures [Ta 02]

Unifying Role of Extractors are intimately related to: • Hash Functions [ILL 89, SZ 94, GW 94] • Expander Graphs [NZ 93, WZ 93, GW 94, RVW 00, TUZ 01, CRVW 02] • Samplers [G 97, Z 97] • Pseudorandom Generators [Trevisan 99, …] • Error-Correcting Codes [T 99, TZ 01, TZS 01, SU 01, U 02] Unify theory of pseudorandomness.

Definitions

Weak random sources Distributions X on {0, 1}n with some entropy: • [v. N] sources: n coins of unknown fixed bias • [SV] sources: Pr[Xi+1 =1|X 1=b 1, …, Xi=bi] (δ, 1 -δ) • Bit fixing: n coins, some good, some “sticky” • …. . • [Z] k-sources: H∞(X) ≥ k x Pr[X = x] 2 -k e. g X uniform with support 2 k {0, 1}n X

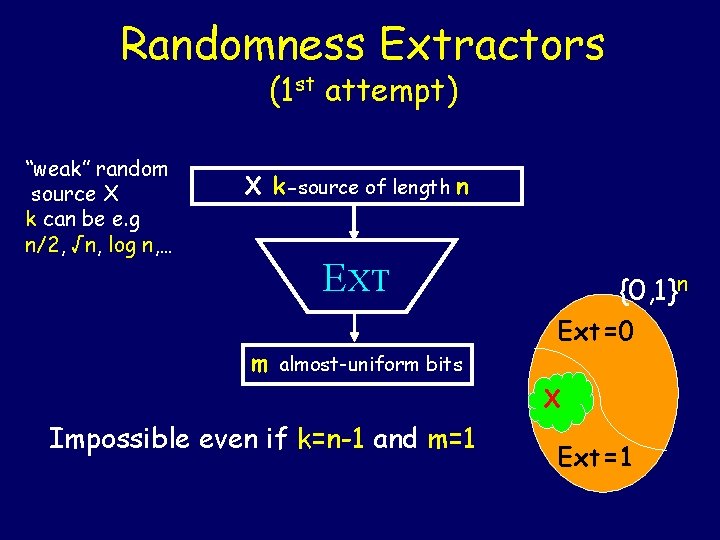
Randomness Extractors (1 st attempt) “weak” random source X k can be e. g n/2, √n, log n, … X k-source of length n EXT m almost-uniform bits {0, 1}n Ext=0 X Impossible even if k=n-1 and m=1 Ext=1

Extractors [Nisan & Zuckerman `93] X k-source of length n (short) “seed” d random bits EXT m almost-uniform bits • Ext : {0, 1}n x {0, 1}d {0, 1}m • X has min-entropy k ( X is a k-source) • m ≤ k+d

Extractors [Nisan & Zuckerman `93] k-source of length n (short) “seed” d random bits EXT X {0, 1}n y {0, 1}d m bits -close to uniform k-source X, | Ext(X, Ud) – Um|1 < but -fraction of y’s, | Ext(X, y) – Um|1 < Ext(X, y) {0, 1}m

Extractors as graphs (k, )-extractor Ext: {0, 1}n {0, 1}d {0, 1}m {0, 1}n {0, 1}m Sampling Hashing Amplification Coding Expanders k-source X x k |X|=2 y … (X) Ext(x, y) B Discrepancy: For all but 2 k of the x {0, 1}n, | | (X) B|/2 d - |B|/2 m |<

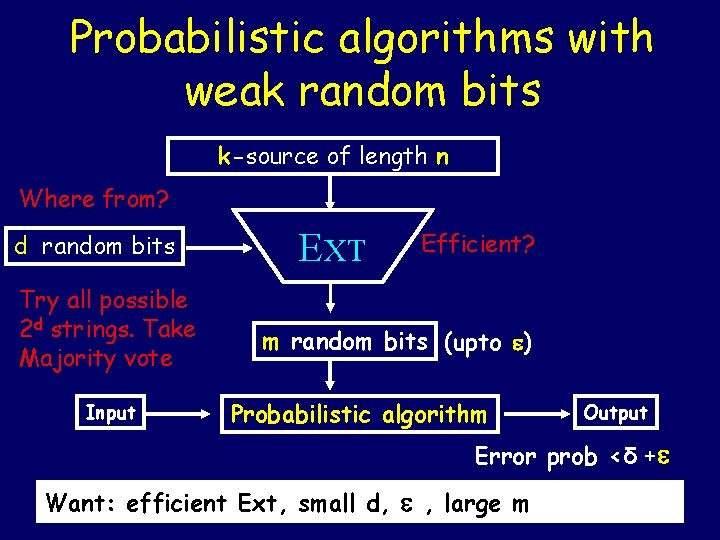
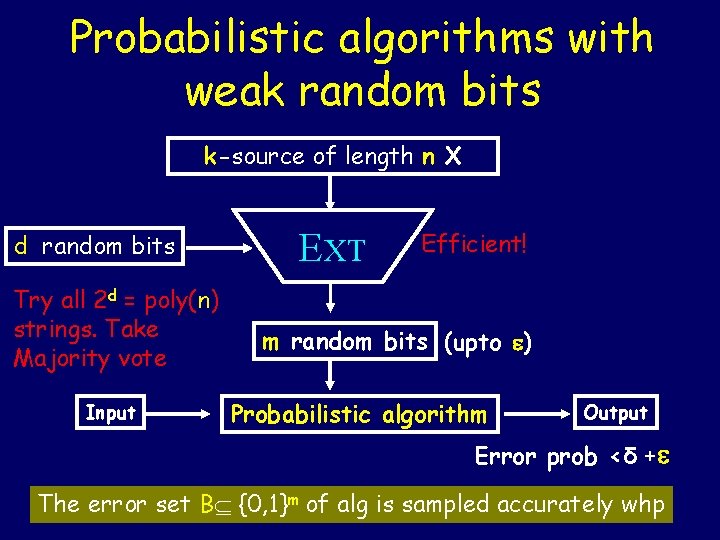
Probabilistic algorithms with weak random bits k-source of length n Where from? d random bits Try all possible 2 d strings. Take Majority vote Input EXT Efficient? m random bits (upto ) Probabilistic algorithm Output Error prob <δ + Want: efficient Ext, small d, , large m

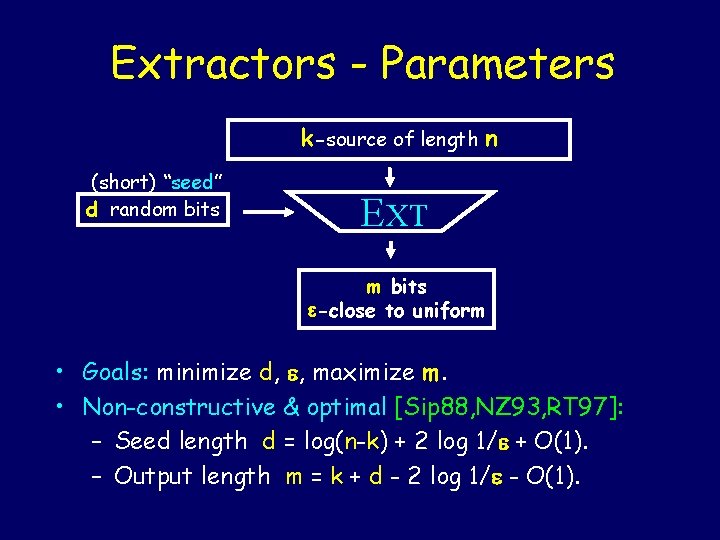
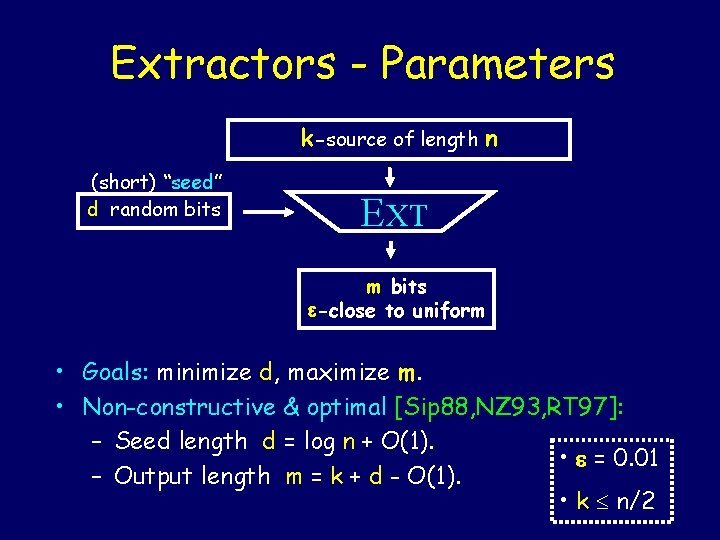
Extractors - Parameters k-source of length n (short) “seed” d random bits EXT m bits -close to uniform • Goals: minimize d, , maximize m. • Non-constructive & optimal [Sip 88, NZ 93, RT 97]: – Seed length d = log(n-k) + 2 log 1/ + O(1). – Output length m = k + d - 2 log 1/ - O(1).

Extractors - Parameters k-source of length n (short) “seed” d random bits EXT m bits -close to uniform • Goals: minimize d, maximize m. • Non-constructive & optimal [Sip 88, NZ 93, RT 97]: – Seed length d = log n + O(1). • = 0. 01 – Output length m = k + d - O(1). • k n/2

Explicit Constructions Non-constructive & optimal [Sip 88, NZ 93, RT 97]: – Seed length d = log n + O(1). – Output length m = k + d - O(1). [. . . B 86, SV 86, CG 87, NZ 93, WZ 93, GW 94, SZ 94, SSZ 95, Zuc 96, Ta 98, Tre 99, RRV 99 a, RRV 99 b, ISW 00, RVW 00, TUZ 01, TZS 01, SU 01, LRVW 03, …] New explicit constructions [GUV 07, DW 08] - Seed length d = O(log n) [even for =1/n] – Output length m =. 99 k + d

Applications

Probabilistic algorithms with weak random bits k-source of length n X d random bits Try all 2 d = poly(n) strings. Take Majority vote Input EXT Efficient! m random bits (upto ) Probabilistic algorithm Output Error prob <δ + The error set B {0, 1}m of alg is sampled accurately whp

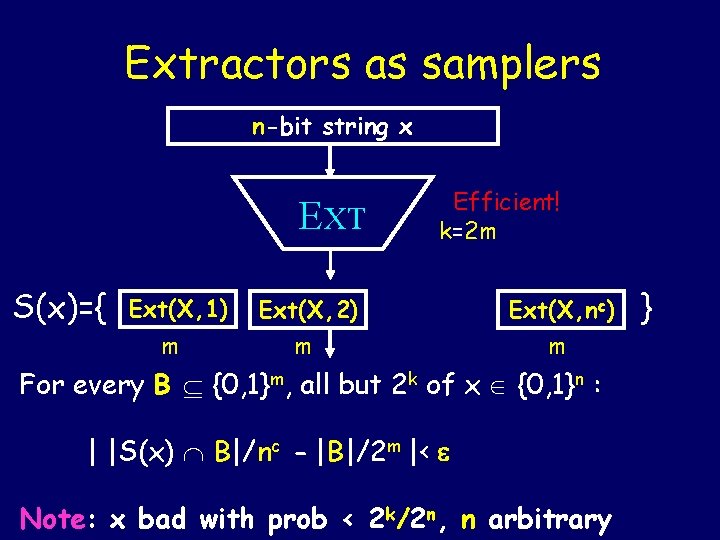
Extractors as samplers n-bit string x EXT S(x)={ Ext(X, 1) m Efficient! k=2 m Ext(X, 2) m Ext(X, nc) m For every B {0, 1}m, all but 2 k of x {0, 1}n : | |S(x) B|/nc - |B|/2 m |< Note: x bad with prob < 2 k/2 n, n arbitrary }

{0, 1} Extractors as list-decodable error-correcting codes [TZ] D c 8 c 9 c 1 c 2 c 7 c 6 C(x)= C: {0, 1}n {0, 1}D c 3 z c 5 c 4 Ext(X, 1) 1 bit n-bit string x EXT Ext(X, 2) 1 bit ……… d = c log n D =2 d = nc Polynomial rate! Efficient encoding!! Efficient decoding? Ext(X, D) 1 bit For z {0, 1}D let Bz {0, 1}d+1 be the set {(i, zi) : i [D] } List decoding: For every z, at most D 2 of x have C(x) fall in (1/2 - )D hamming ball around z

Beating e-value expansion Task: Construct an graph on [N] of minimal degree DEG s. t. every two sets of size K are connected by an edge. Any such graph: DEG > N/K K Ramanujan graphs: DEG < (N/K)2 Random graphs: DEG < (N/K)1+o(1) Extractors: DEG < (N/K)1+o(1) K linear in N and constant DEG [RVW] We’ll see it for “moderate” K N [WZ] K

Extractors as graphs (again) (k, . 01)-extractor 2 k = K = M 1+o(1) 2 d = D < Mo(1) Take G = Ext 2 on [N] DEG < (N/K)1+o(1) Many edges between any two K-sets X, X’ Ext: {0, 1}n {0, 1}d {0, 1}m Ext: [N] x [D] [M] [N] |X|=K [M] | (X)| >. 99 M |X’|=K

Constructions

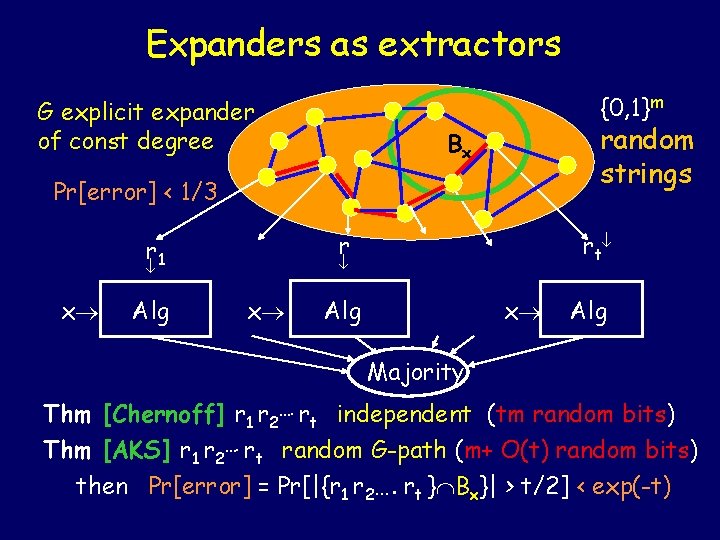
Expanders as extractors {0, 1}m G explicit expander of const degree random strings Bx Pr[error] < 1/3 r r 1 x Alg r t x Alg Majority Thm [Chernoff] r 1 r 2…. rt independent (tm random bits) Thm [AKS] r 1 r 2…. rt random G-path (m+ O(t) random bits) then Pr[error] = Pr[|{r 1 r 2…. rt } Bx}| > t/2] < exp(-t)

Expanders as extractors (k large) G expander graph of const degree on {0, 1}m B any subset, δ=|B|/2 m S = {r 1 r 2…. rt} a random G-path (n = m+ O(t) bits) Thm [G] Pr[| δ - |S B|/t | > ] < exp(- 2 t) Thm [Z] t=cm=2 d, Ext : {0, 1}n x {0, 1}d {0, 1}m Ext(r 1 r 2…. rt ; i) = ri is an (k=. 99 n, )–extractor of d=O(log n) seed

Condensers [RR 99, RSW 00, TUZ 01] X k-source of length n seed d random bits Con. 99 k-source of length k Sufficient to construct such condensers: from here we can use [Z] extractor

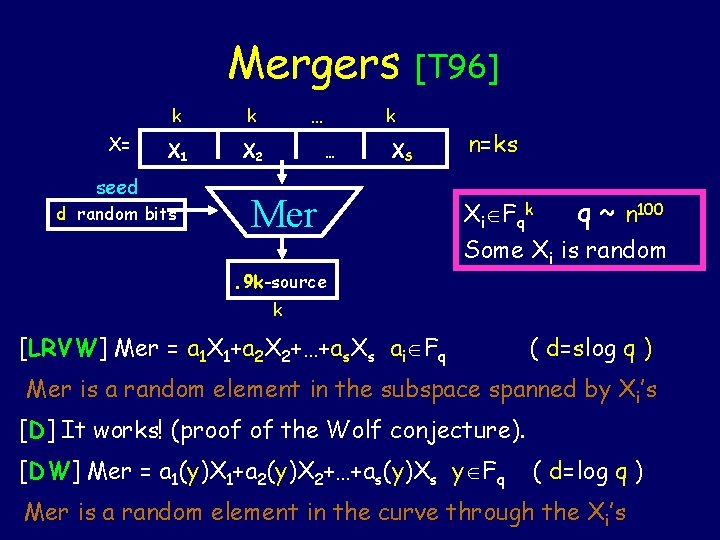
Mergers X= k k X 1 X 2 [T 96] … k … XS n=ks seed d random bits Mer. 9 k-source k Some block Xi is random. The other Xj are correlated arbitrarily with it. Mer outputs a high entropy distribution.

Mergers X= k k X 1 X 2 seed d random bits … [T 96] k … XS Mer. 9 k-source n=ks Xi Fqk q ~ n 100 Some Xi is random k [LRVW] Mer = a 1 X 1+a 2 X 2+…+as. Xs ai Fq ( d=slog q ) Mer is a random element in the subspace spanned by X i’s [D] It works! (proof of the Wolf conjecture). [DW] Mer = a 1(y)X 1+a 2(y)X 2+…+as(y)Xs y Fq ( d=log q ) Mer is a random element in the curve through the Xi’s

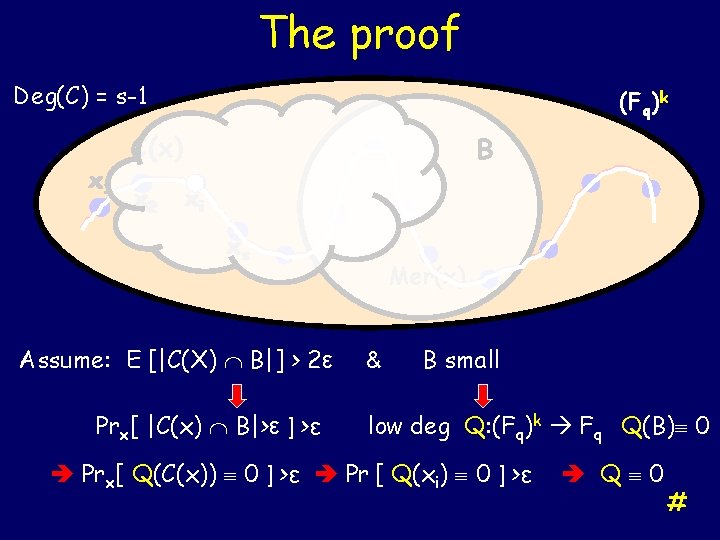
The proof Deg(C) = s-1 x 11 (Fq)k C(x) x 22 B xii xss Assume: E [|C(X) B|] > 2ε Prx[ |C(x) B|>ε ] >ε Mer(x) & B small low deg Q: (Fq)k Fq Q(B) 0 Prx[ Q(C(x)) 0 ] >ε Pr [ Q(xi) 0 ] >ε Q 0 #

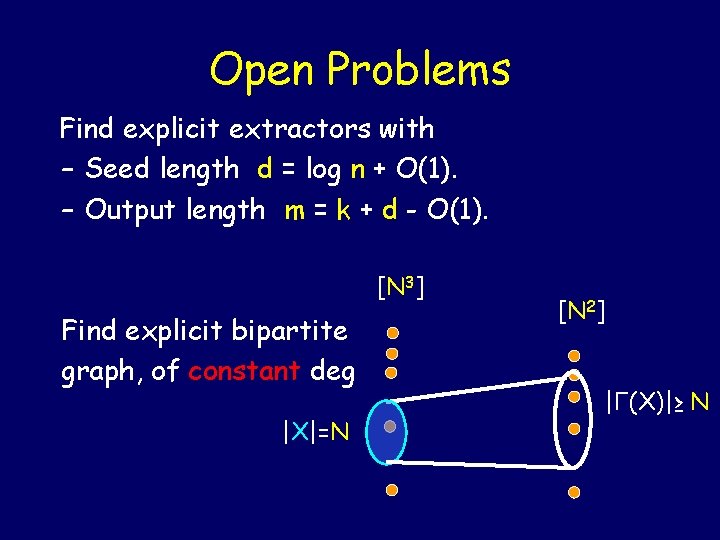
Open Problems Find explicit extractors with – Seed length d = log n + O(1). – Output length m = k + d - O(1). [N 3] Find explicit bipartite graph, of constant deg |X|=N [N 2] |Γ(X)|≥ N

Extractors as samplers Given B {0, 1}m Estimate |B|/2 m X k-source of length n d random bits EXT Efficient! m random bits (upto ) Try all 2 d = poly(n) strings. Count the fraction falls in B Any set B {0, 1}m WHP estimation error <