Randomized pivoting rules for the simplex algorithm upper

Randomized pivoting rules for the simplex algorithm – upper and lower bounds Uri Zwick (武熠) – Tel Aviv University AAAC 2018 Asian Association for Algorithms and Computation

Linear Programming Maximize a linear objective function subject to a set of linear inequalities (and equalities) Find the highest point in a polyhedron

The Simplex Algorithm [Dantzig (1947)] Start at some vertex. Move up, from vertex to vertex, along edges, until reaching the top.

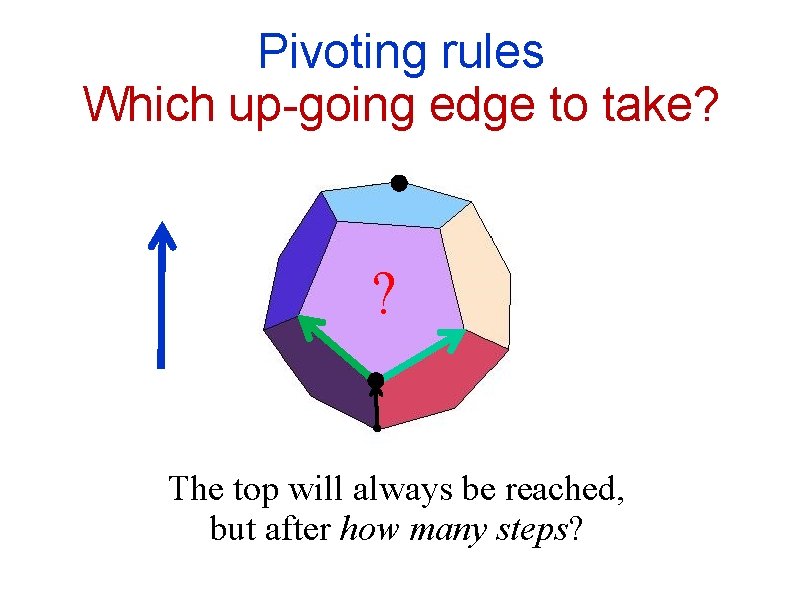
Pivoting rules Which up-going edge to take? ? The top will always be reached, but after how many steps?

Deterministic pivoting rules Largest improvement Largest slope Dantzig’s rule – Largest modified cost Bland’s rule (avoids cycling) Lexicographic rule (also avoids cycling) Zadeh’s rule – “least recently entered” All known deterministic pivoting rules require an exponential number of steps, in the worst-case [Klee-Minty (1972)] , … , [Amenta-Ziegler (1996)] [Friedmann (2011)]

Algorithms for Linear Programming Simplex [Dantzig 1947] No polynomial version known (yet? ) Polynomial, but not strongly polynomial Not “combinatorial”

Is the simplex algorithm still interesting? The simplex algorithm works very well in practice. Fundamental and intriguing open problems: 1. Is there a polynomial pivoting rule? 2. Is the diameter polynomial? 3. Is Linear Programming strongly polynomial? Simplex-like algorithms can be used to solve more than just LP problems.

Turn-based 2 -Player 0 -Sum Stochastic Games [Shapley ’ 53] [Gillette ’ 57] … [Condon ’ 92] States are divided between two players, max and min. From each state, there is a collection of available probabilistic actions, each with an associated reward. Players try to maximize/minimize total expected reward. Both players have optimal positional strategies Can optimal strategies be found in polynomial time? Best known algorithm is a sub-exponential simplex-like algorithm

Markov Decision Processes [Shapley ’ 53] [Bellman ’ 57] [Howard ’ 60] … When there is only one player, the game is known as a Markov Decision Process. The game ends when the token reaches the sink. Optimal positional strategies can be found using LP Is there a strongly polynomial time algorithm?

Diameter of polytopes Hirsch Conjecture (1957) Refuted! [Santos (2010)] Diameter is still believed to be polynomial Quasi-polynomial upper bound [Kalai-Kleitman (1992)] ([Todd (2014)])

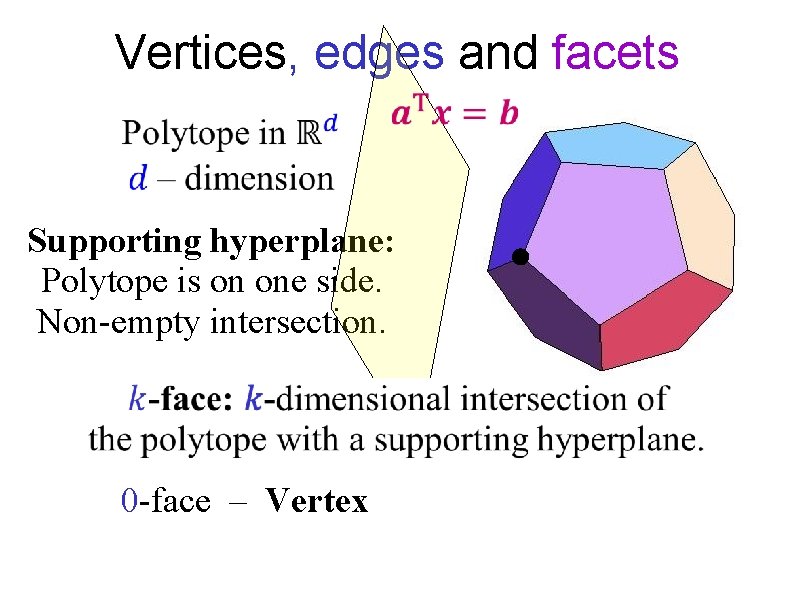
Vertices, edges and facets Supporting hyperplane: Polytope is on one side. Non-empty intersection. 0 -face – Vertex

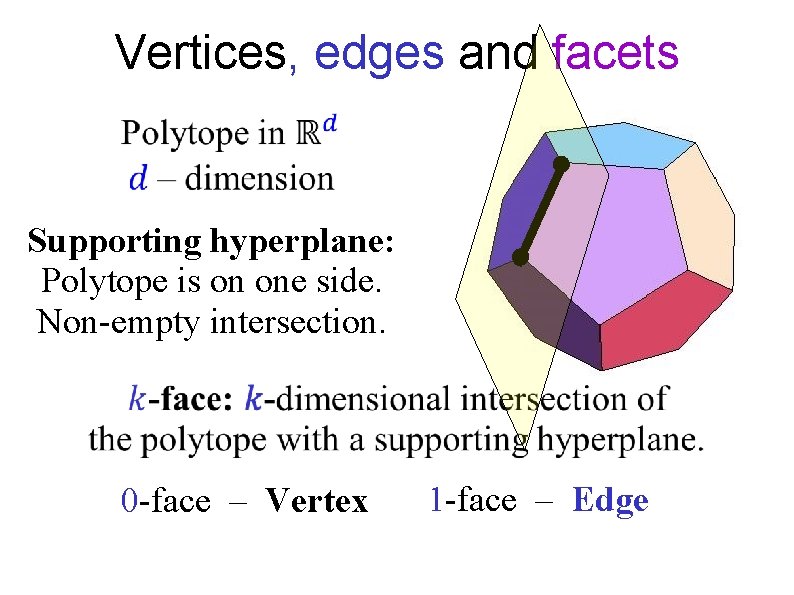
Vertices, edges and facets Supporting hyperplane: Polytope is on one side. Non-empty intersection. 0 -face – Vertex 1 -face – Edge

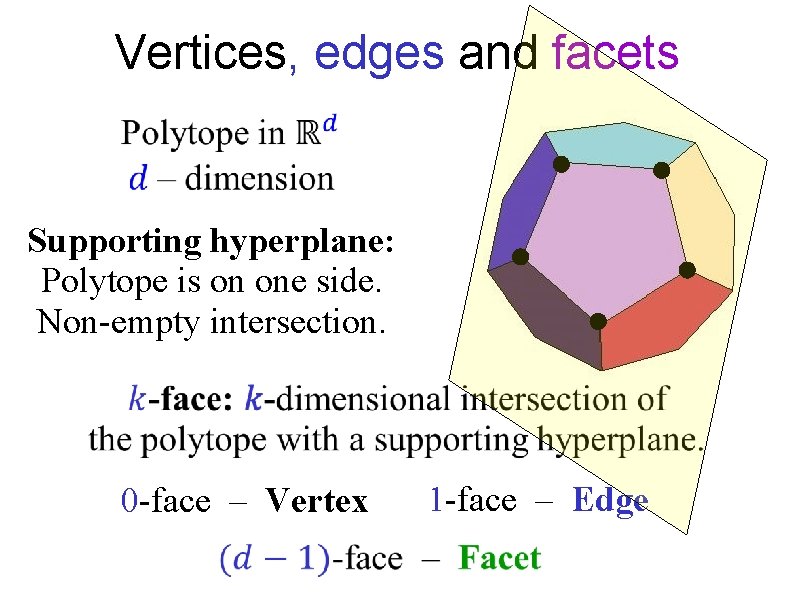
Vertices, edges and facets Supporting hyperplane: Polytope is on one side. Non-empty intersection. 0 -face – Vertex 1 -face – Edge

Randomized pivoting rules Random-Edge Choose a random improving edge [Dantzig (1947)] Random-Facet [Kalai (1992)] [Matoušek-Sharir-Welzl (1992)] To be described shortly Random-Facet is sub-exponential!

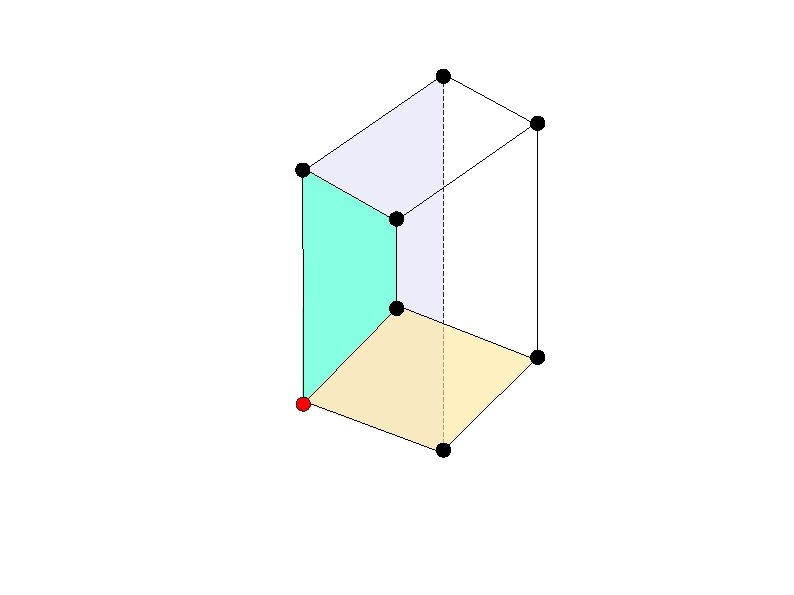
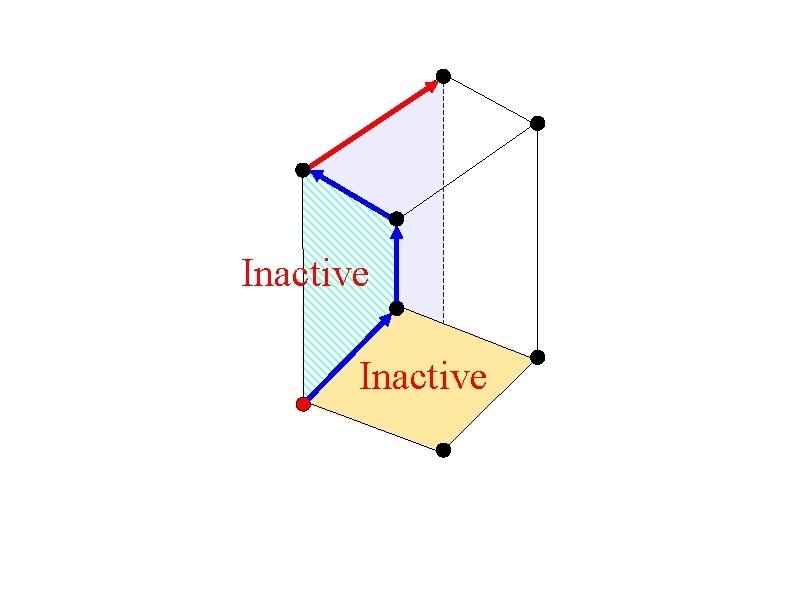
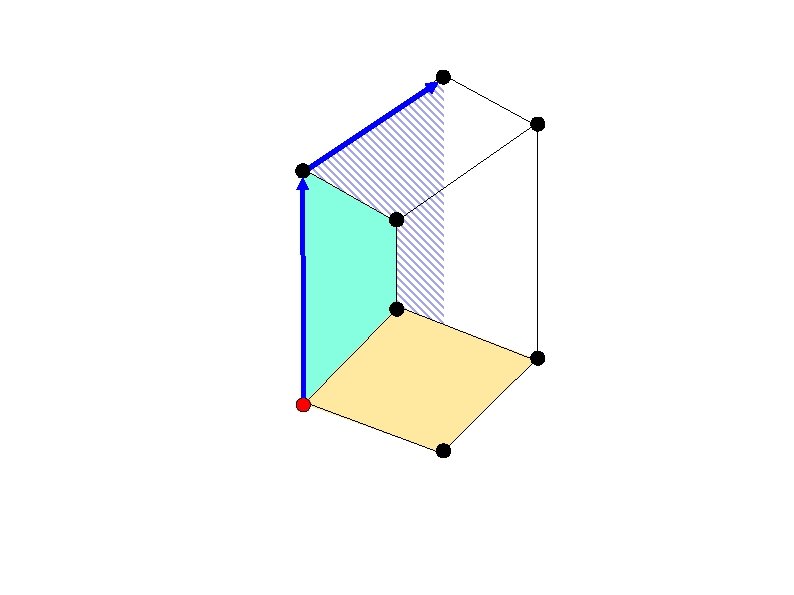
Primal Random-Facet [Kalai (1992)]

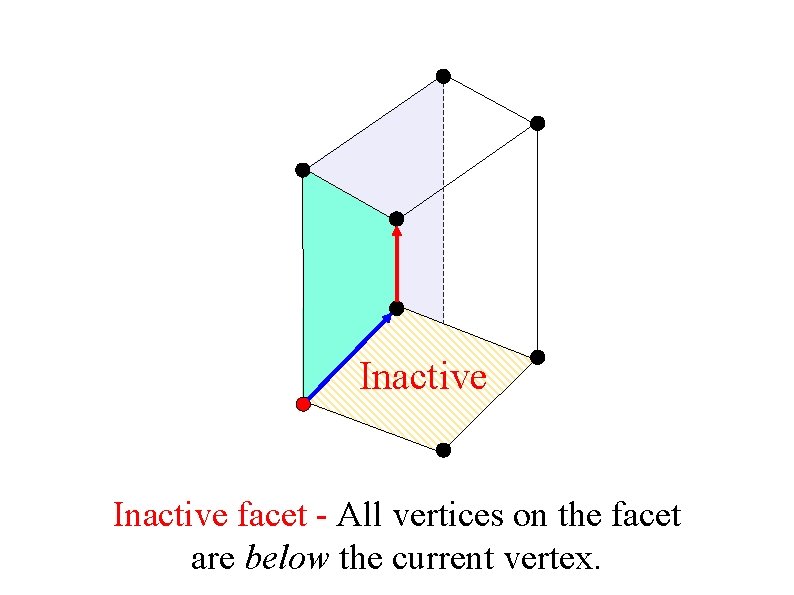
Inactive facet - All vertices on the facet are below the current vertex.

Inactive

Primal Random-Facet [Kalai (1992)]

Unusual recurrence relations Unusual 2 D recurrence relations are much harder to analyze, but exhibit similar behavior.

Linear Programming Duality

Linear Programming Duality d variables n inequalities

Dual Random-Facet [Matoušek-Sharir-Welzl (1992)] § Choose a random facet not containing the current (infeasible) basic solution (bs). § Solve recursively without this facet, starting from the current basic solution. § If the bs obtained is on the right side of the ignored facet, i. e. , is a vertex, we are done. § Otherwise, do a dual pivoting step to a basic solution on the ignored facet and recurse.

Improved Random-Facet [Kalai (1992) (1996)] [Gärtner (1995)] [Hansen-Z (2014)] Improved Random-Facet is (almost) a primal algorithm. It is faster than both Primal and Dual Random-Facet. Improved either follows an edge to an adjacent vertex, or jumps back to a previously visited vertex. Improved Random-Facet defines a tree, rather than a path.

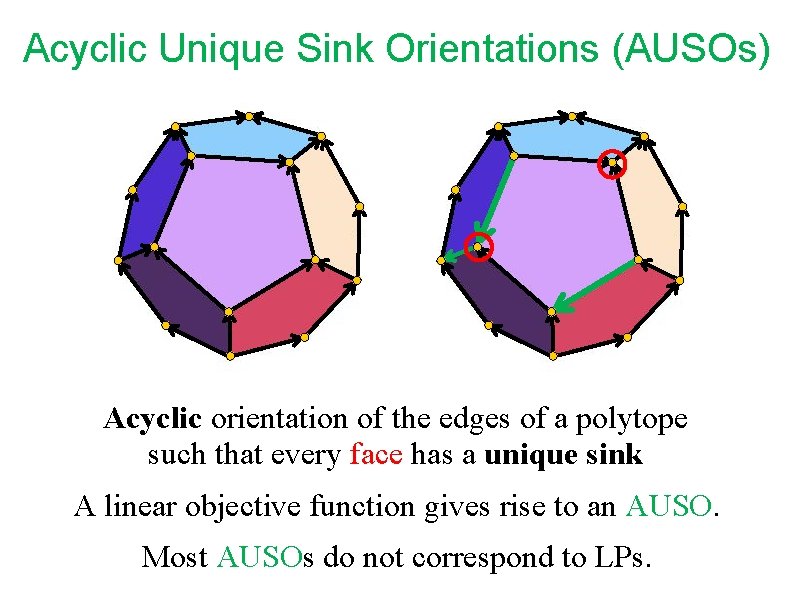
Acyclic Unique Sink Orientations (AUSOs) Acyclic orientation of the edges of a polytope such that every face has a unique sink A linear objective function gives rise to an AUSO. Most AUSOs do not correspond to LPs.

Random-Facet on AUSOs The analysis of Random-Facet only uses the AUSO properties. The 2 -player stochastic games define AUSOs. Thus, they can be solved using Random-Facet. Does Random-Facet run faster on LPs? Random-Facet is not polynomial, even for LPs.

(Sub-)Exponential lower bounds Random Edge and Random Facet [Friedmann-Hansen-Z (2011, 2014)] Random-Edge and Random-Facet are not polynomial even on LPs. Lower bound for Random-Edge obtained on an LP corresponding to a Markov Decision Process (MDP) Lower bound for Random-Facet obtained on an LP corresponding to a Shortest Path problem.

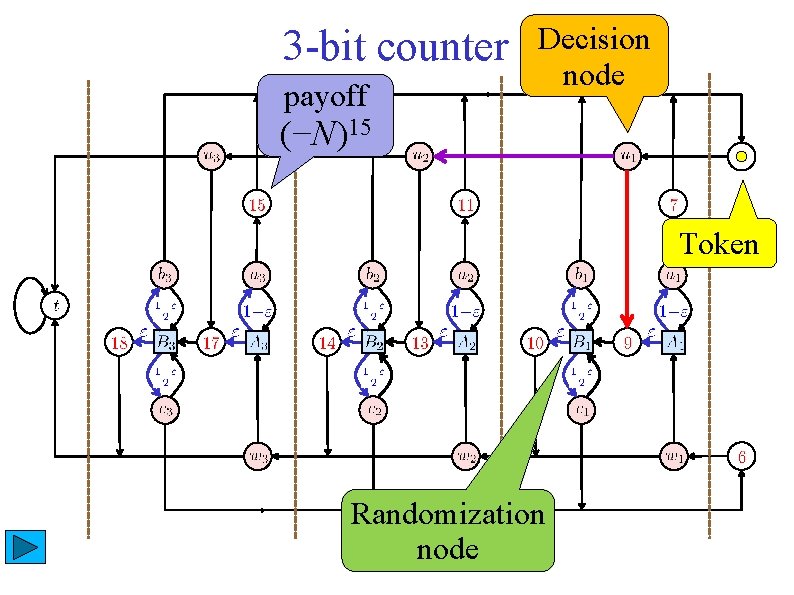
3 -bit counter payoff Decision node (−N)15 Token Randomization node

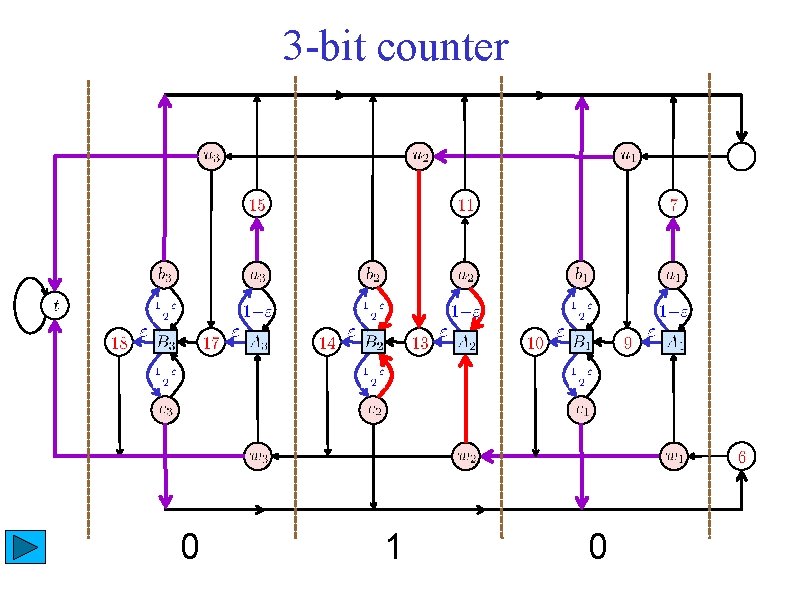
3 -bit counter 0 1 0

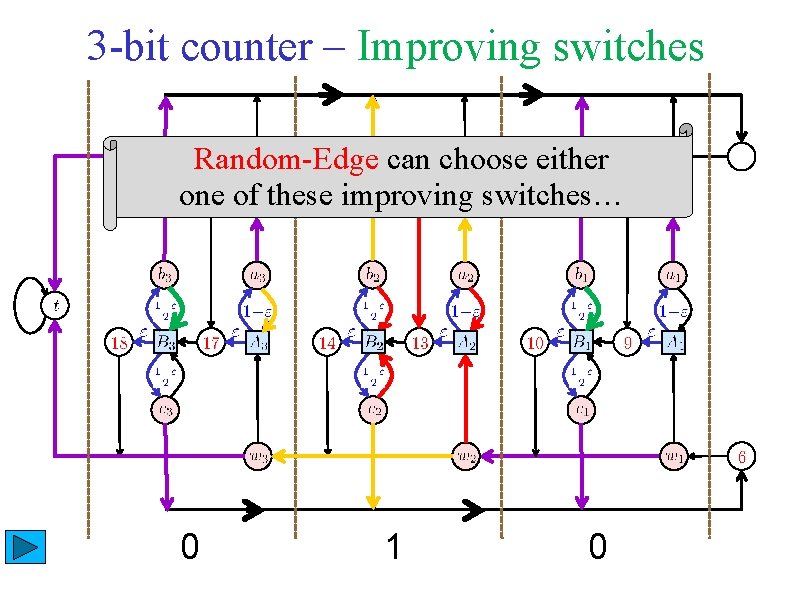
3 -bit counter – Improving switches Random-Edge can choose either one of these improving switches… 0 1 0

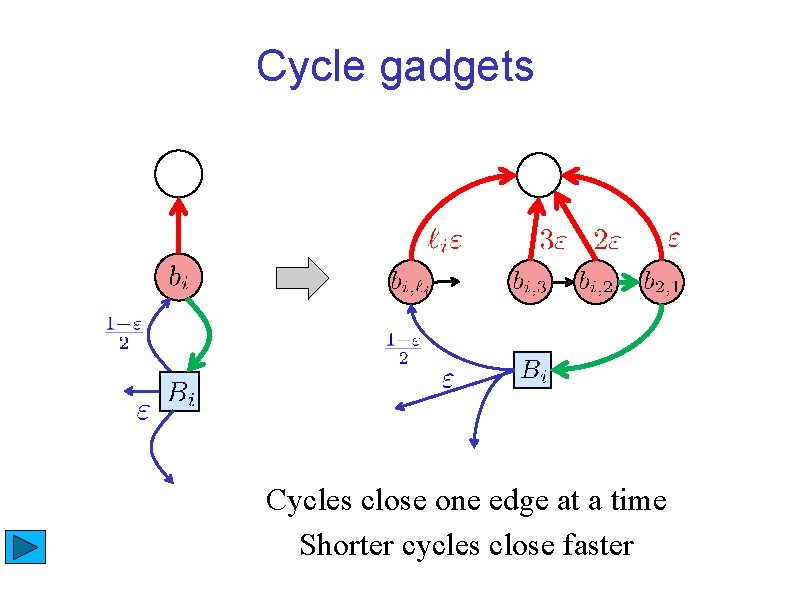
Cycle gadgets Cycles close one edge at a time Shorter cycles close faster

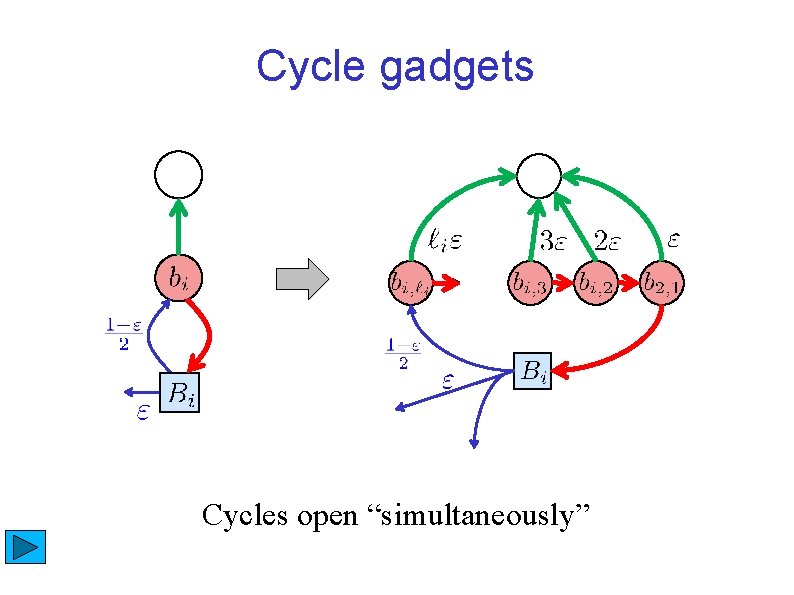
Cycle gadgets Cycles open “simultaneously”

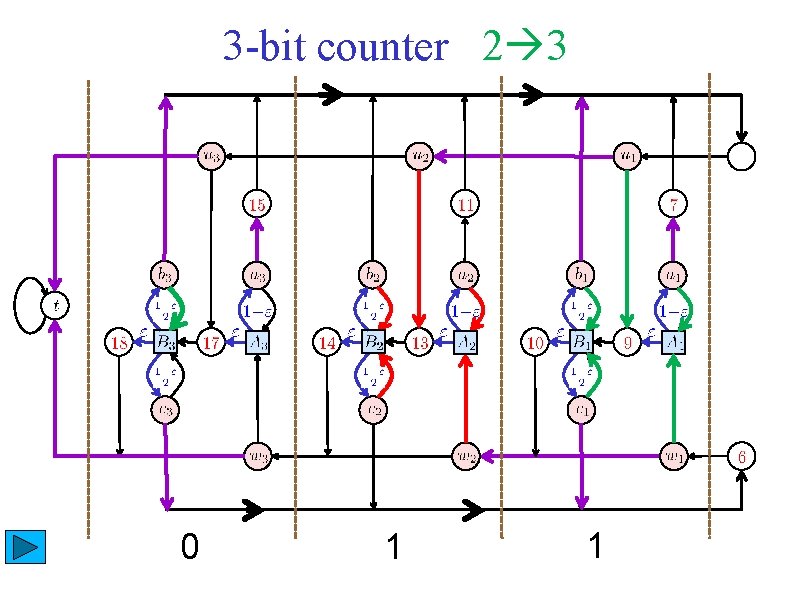
3 -bit counter 2 3 0 1 10

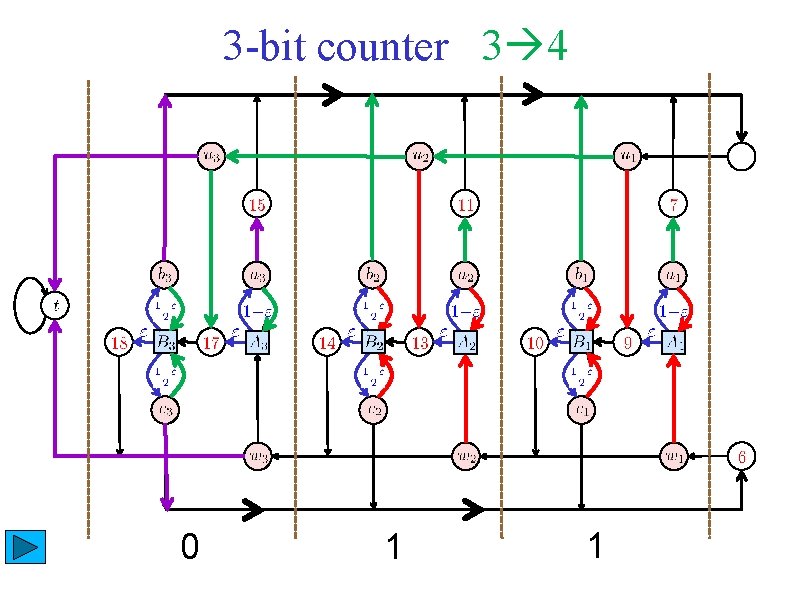
3 -bit counter 3 4 0 1 1

Size of cycles Various cycles and lanes compete with each other Some are trying to open while some are trying to close We need to make sure that our candidates win! Can be improved using a more complicated construction and an improved analysis (work in progress)

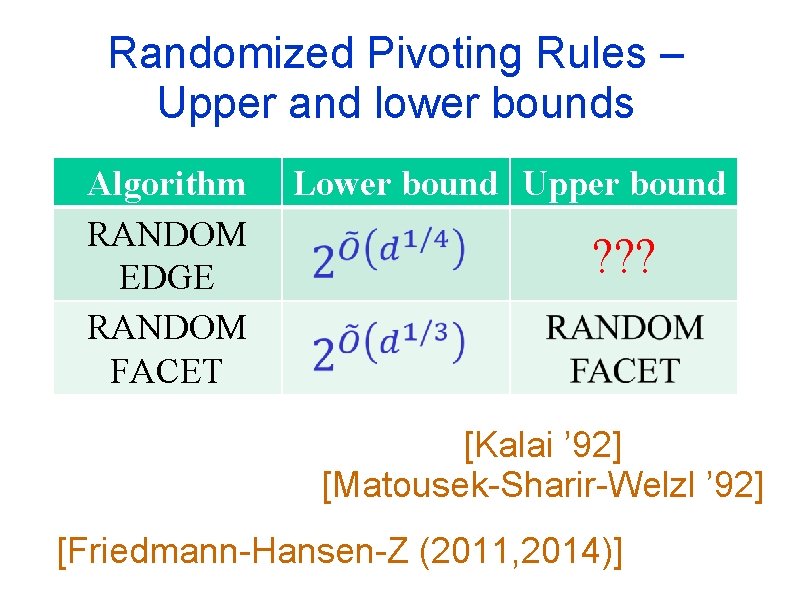
Randomized Pivoting Rules – Upper and lower bounds Algorithm RANDOM EDGE RANDOM FACET Lower bound Upper bound ? ? ? [Kalai ’ 92] [Matousek-Sharir-Welzl ’ 92] [Friedmann-Hansen-Z (2011, 2014)]

Algorithm RANDOM EDGE RANDOM FACET Lower bound Upper bound [Hansen-Z (2016)] [Hansen-Paterson-Z (2014)] [Matousek (1994)] [Gärtner (2002)]

Algorithm RANDOM EDGE RANDOM FACET Lower bound Upper bound

Concluding remarks and open problems Is there a polynomial pivoting rule? Is the diameter polynomial? Is Linear Programming strongly polynomial? Are there better randomized pivoting rules? Is Random-Edge subexponential? Subexponential lower bound for Improved-Random-Facet? Are there deterministic subexponential pivoting rules? Faster algorithms for Turn-based 2 -Player 0 -Sum Stochastic Games?