Randomized algorithms Hiring problem We always want the

Randomized algorithms Hiring problem We always want the best hire for a job! • Using employment agency to send one candidate at a time • Each day, we interview one candidate • We must decide immediately if to hire candidate and if so, fire previous In other words … • Always want the best hire… • Cost to interview (low) • Cost to fire/hire… (expensive) CSC 317 1

Hire-Assistant(n) 1. best = 0 //least qualified candidate 2. for i = 1 to n 3. interview candidate i 4. if candidate i better than best 5. best = i 6. hire candidate i • Always want the best hire… fire if better candidate comes along • Cost to interview (low) Ci • Cost to fire/hire… (expensive) Ch n total number of candidates m total number of hires Ch > C i O (? ) CSC 317 2

Hire-Assistant(n) 1. best = 0 //least qualified candidate 2. for i = 1 to n 3. interview candidate i 4. if candidate i better than best 5. best = i 6. hire candidate i • Always want the best hire… fire if better candidate comes along • Cost to interview (low) Ci • Cost to fire/hire… (expensive) Ch n total number of candidates m total number of hires Ch > C i O (? ) different cost of hiring Not run time but cost of hiring, but flavor of max problem CSC 317 3

• Always want the best hire… fire if better candidate comes along • Cost to interview (low) Ci • Cost to fire/hire… (expensive) Ch Ch > C i n total number of candidates m total number of hires O (cin + chm) Different type of cost – not run time, but cost of hiring. But when is it most expensive? When candidates interview in reverse order, worst first… CSC 317 4

Hiring problem 1. best = 0 //least qualified candidate 2. for i = worst_candidate to best_candidate… O (cin + chn) = O(chn) When is this most expensive? When candidates interview in reverse order, worst first… CSC 317 5

• Always want the best hire… fire if better candidate comes along • Cost to interview (low) Ci • Cost to fire/hire… (expensive) Ch Ch > C i n total number of candidates m total number of hires When is it least expensive? CSC 317 6

Hiring problem 1. best = 0 //least qualified candidate 2. for i = best_candidate to worst_candidate… O (cin + ch) When is this leat expensive? When candidates interview in order, best first… But we don’t know who is best a priori CSC 317 7

Hiring problem • • Cost to interview (low Ci) Cost to fire/hire … (expensive Ch) n number of candidates m hired O (cin + chm) depends on order of candidates Independent of order of candidates What about if we randomly invite candidates? CSC 317 8

Hiring problem and randomized algorithms O (cin + chm) depends on order of candidates • Can’t assume in advance that candidates are in random order – bias might exist. • We can add randomization to our algorithm – by asking the agency to send names in advance and randomize CSC 317 9

Hiring problem - randomized We always want the best hire for a job! • Employment agency sends list of n candidates in advance • Each day, we choose randomly a candidate from the list to interview • We do not rely on the agency to send us randomly, but rather take control in algorithm CSC 317 10

Randomized hiring problem(n) 1. randomly permute the list of candidates 2. Hire-Assistant(n) What do we mean by randomly permute (we need a random number generator)? Random(a, b) Function that returns an integer between a and b, inclusive, where each integer has equal probability Most programs: pseudorandom-number generator CSC 317 11

Including random number generator Random(a, b) Function that returns an integer between a and b, inclusive, where each integer has equal probability So, Random(0, 1)? 0 with P = 0. 5 1 with P = 0. 5 CSC 317 12

Including random number generator Random(a, b) Function that returns an integer between a and b, inclusive, where each integer has equal probability So, Random(3, 7)? 3 with P = 0. 2 4 with P = 0. 2 5 with P = 0. 2 6 with P = 0. 2 7 with P = 0. 2 Like rolling a (7 -3+1) dice CSC 317 13

How do we random permutations? Randomize-in-place(A, n) 1. For i = 1 to n 2. swap A[i] with A[Random(i, n)] i Random choice from A[i, …, n] A=123456 A=321456 A=361452 … CSC 317 14

Probability review • Sample space S: space of all possible outcomes (e. g. that can happen in a coin toss) • Probability of each outcome: p(i) ≥ 0 • Example: coin toss S = {H, T} CSC 317 15

Probability review • Event: a subset of all possible outcomes; subset of sample space S • Probability of event: • Example: coin toss that give heads E = {H} • Example: rolling two dice CSC 317 16

Probability review Example: rolling two dice • List all possible outcomes S={(1, 1}, (1, 2), (1, 3), …(2, 1), (2, 2), (2, 3), …(6, 6)} • List the event or subset of outcomes for which the sum of the dice is 7 E = {(1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3)} • Probability of event that sum of dice 7: 6/36 = 1/6 CSC 317 17

Probability review • Random variable: attaches value to an outcome/s Example: value of one dice Example: sum of two dice P(X = x): Probability that random variable X takes on value x random variable value of random variable P(X = x): Probability that sum of two dice has value x, e. g. P(X = 7) = 1/6 CSC 317 18

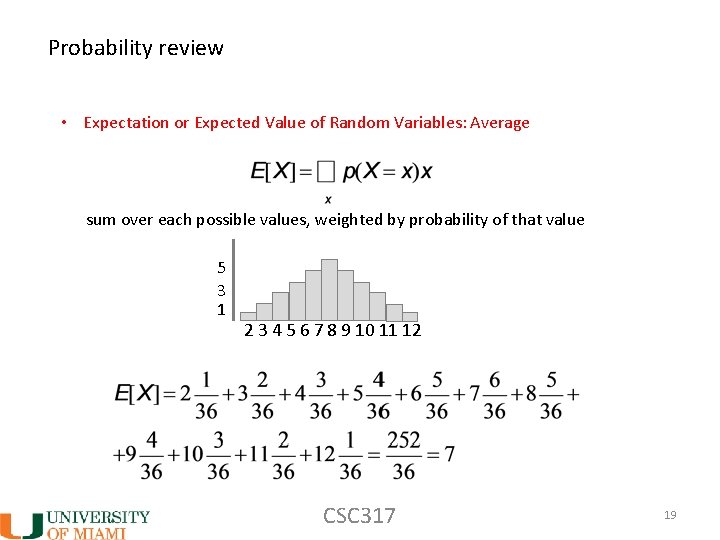
Probability review • Expectation or Expected Value of Random Variables: Average sum over each possible values, weighted by probability of that value 5 3 1 2 3 4 5 6 7 8 9 10 11 12 CSC 317 19

Easier way? • Linearity of Expectation random variables, then: Does not require independence of random variables. Example: X 1 and X 2 represent the values of a dice CSC 317 20

Probability review • Indicator Random Variable (indicating if occurs…) if A occurs vice versa Lemma: For event A Example: Expected number Heads when flipping fair coin CSC 317 21

Probability review • Indicator Random Variable & Linearity of Expectation if A occurs vice versa Example: Expected number Heads when flipping 3 fair coins CSC 317 22