Randomized Algorithms CS 648 Lecture 2 Randomized Algorithm




![Approximate median Definition: Given an array A[] storing n numbers and ϵ > 0, Approximate median Definition: Given an array A[] storing n numbers and ϵ > 0,](https://slidetodoc.com/presentation_image_h2/0a08cb7e2cf03f799dda8bf7d36b6991/image-5.jpg)














- Slides: 25

Randomized Algorithms CS 648 Lecture 2 • Randomized Algorithm for Approximate Median • Elementary Probability theory 1

RANDOMIZED MONTE CARLO ALGORITHM FOR APPROXIMATE MEDIAN This lecture was delivered at slow pace and its flavor was that of a tutorial. Reason: To show that designing and analyzing a randomized algorithm demands right insight and just elementary probability. 2

A simple probability exercise • 3

![Approximate median Definition Given an array A storing n numbers and ϵ 0 Approximate median Definition: Given an array A[] storing n numbers and ϵ > 0,](https://slidetodoc.com/presentation_image_h2/0a08cb7e2cf03f799dda8bf7d36b6991/image-5.jpg)
Approximate median Definition: Given an array A[] storing n numbers and ϵ > 0, compute an element whose rank is in the range [(1 - ϵ)n/2, (1+ ϵ)n/2]. Best Deterministic Algorithm: • “Median of Medians” algorithm for finding exact median • Running time: O(n) • No faster algorithm possible for approximate median Can you give a short proof ? 5

½ - Approximate median A Randomized Algorithm Rand-Approx-Median(A) 1. Let k c log n; 2. S ∅; 3. For i=1 to k 4. x an element selected randomly uniformly from A; 5. S S U {x}; 6. Sort S. 7. Report the median of S. Running time: O(log n loglog n) 6

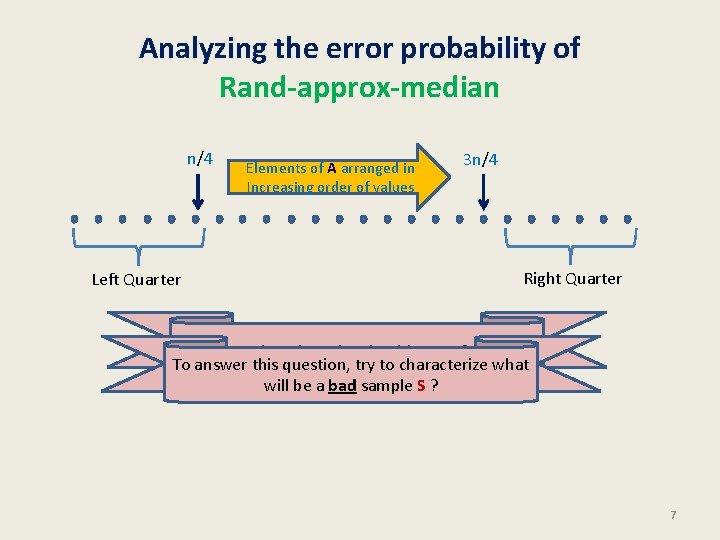
Analyzing the error probability of Rand-approx-median n/4 Left Quarter Elements of A arranged in Increasing order of values 3 n/4 Right Quarter When does the algorithm err ? To answer this question, try to characterize what will be a bad sample S ? 7

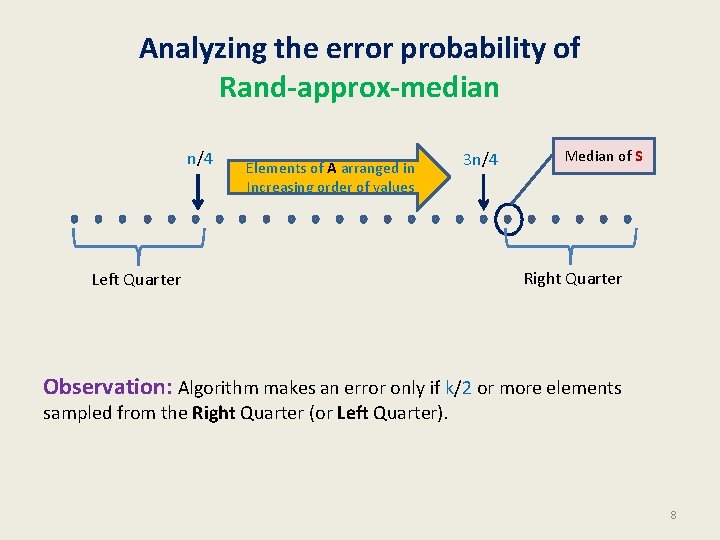
Analyzing the error probability of Rand-approx-median n/4 Elements of A arranged in Increasing order of values Left Quarter 3 n/4 Median of S Right Quarter Observation: Algorithm makes an error only if k/2 or more elements sampled from the Right Quarter (or Left Quarter). 8

Analyzing the error probability of Rand-approx-median • n/4 Elements of A arranged in Increasing order of values 3 n/4 Right Quarter Left Quarter ¼ Exactly the same as the coin tossing exercise we did ! 9

Main result we discussed • 10

ELEMENTARY PROBABILITY THEORY (IT IS SO SIMPLE THAT YOU UNDERESTIMATE ITS ELEGANCE AND POWER) 11

Elementary probability theory (Relevant for CS 648) • We shall mainly deal with discrete probability theory in this course. • We shall take the set theoretic approach to explain probability theory. Consider any random experiment : o Tossing a coin 5 times. o Throwing a dice 2 times. o Selecting a number randomly uniformly from [1. . n]. How to capture the following facts in theory of probability ? 1. Outcome will always be from a specified set. 2. Likelihood of each possible outcome is non-negative. 3. We may be interested in a collection of outcomes. 12

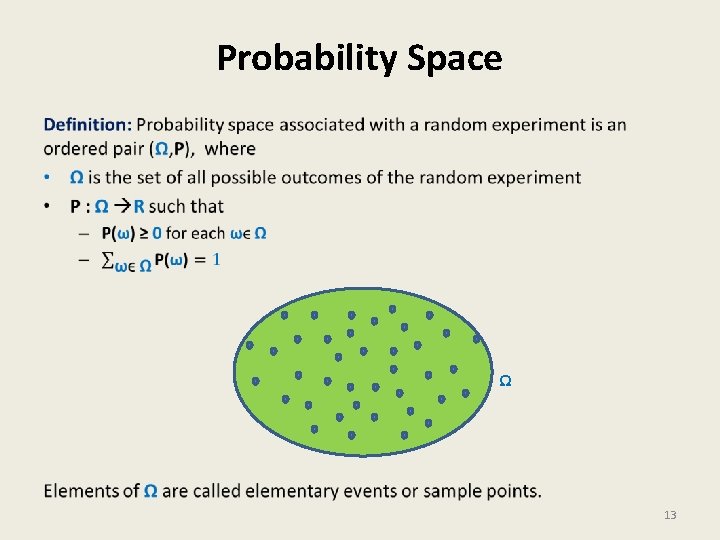
Probability Space • Ω 13

Event in a Probability Space • A Ω 14

Exercises A randomized algorithm can also be viewed as a random experiment. 1. What is the sample space associated with Randomized Quick sort ? 2. What is the sample space associated with Rand-approx-median algorithm ? 15

An Important Advice In the following slides, we shall state well known equations (highlighted in yellow boxes) from probability theory. • You should internalize them fully. • We shall use them crucially in this course. • Make sincere attempts to solve exercises that follow. 16

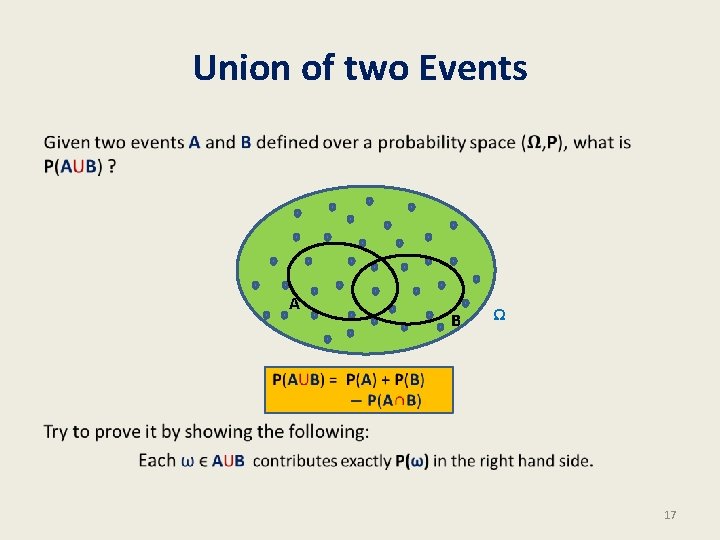
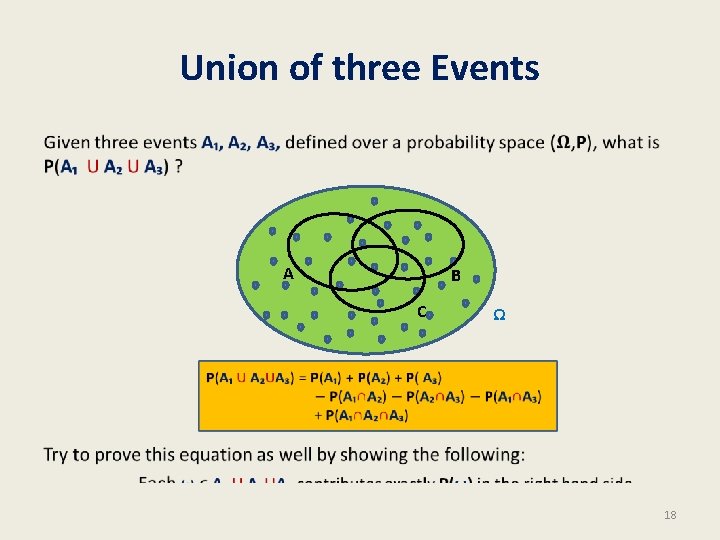
Union of two Events • A B Ω 17

Union of three Events • A B C Ω 18

Exercises • 19

Conditional Probability • 20

Exercises • A man possesses five coins, two of which are double-headed, one is double-tailed, and two are normal. He shuts his eyes, picks a coin at random, and tosses it. What is the probability that the lower face of the coin is a head ? He opens his eyes and sees that the coin is showing heads; what it the probability that the lower face is a head ? He shuts his eyes again, and tosses the coin again. What is the probability that the lower face is a head ? He opens his eyes and sees that the coin is showing heads; what is the probability that the lower face is a head ? He discards this coin, picks another at random, and tosses it. What is the probability that it shows heads ? 21

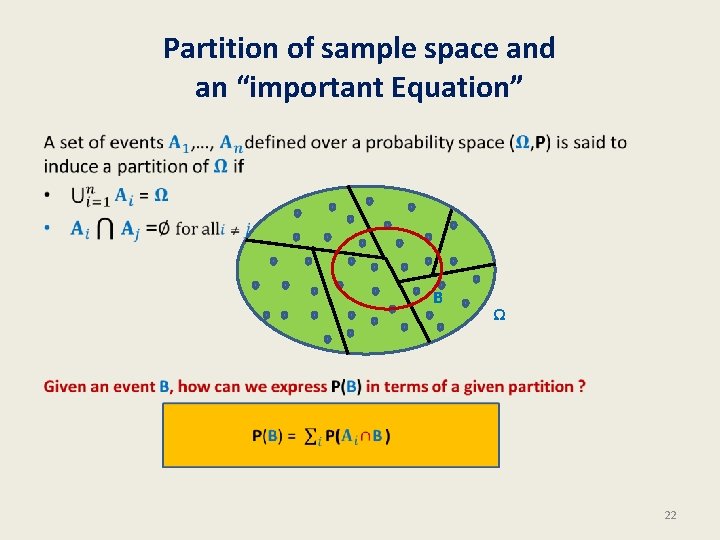
Partition of sample space and an “important Equation” • B Ω 22

Exercises • 23

Independent Events • P(A ∩ B) = P(A) · P(B) 24

Exercises • 25