Randomized Algorithm for Motif Detection Lusheng Wang Dept

Randomized Algorithm for Motif Detection Lusheng Wang Dept. of Computer Science City University of Hong Kong Web: http: //www. cs. cityu. edu. hk/~lwang e-mail: lwang@cs. cityu. edu. hk 2021/12/23 1

Outline: 1. Review our theoretical results 2. A software for motif detection 3. Other problems we have been working --Parametric tools RNA secondary structure comparison --Computing translocation distance between genomes 2021/12/23 2

Distinguishing Substring Selection Problem Instance: Given a set B of n 1 (bad) strings of length at least L, a set G of n 2 (good) strings, two thresholds db and dg ( db < dg). Objective: Find a string s such that for each string b B there exists a substring t of b with length L such that d(s, t) db and for any string g G, d(s, g) dg. Bad sequences s: motif Good sequences 2021/12/23 3

Applications 1. Finding Targets for Potential Drugs (T. Jiang, C. Trendall, S, Wang, T. Wareham, X. Zhang, 98) (K. Lanctot, M. Li, B. Ma, S. Wang, and L. Zhang 1999) -- bad strings in B are from Bacteria. --good strings are from Humans -- find a substring s of length L that is conserved in all bad strings, but not conserved in good strings. -- use s to screen chemicals -- those selected chemicals can then be tested as potential broad-range antibiotics. 2021/12/23 4

Applications 2. Creating Diagnostic Probes for Bacterial Infection (T. Brown, G. A. Leonard, E. D. Booth, G. Kneale, 1990) -- a group of closely related pathogenic bacteria -- find a substring that occurs in each of the bacterial sequences (with as few substitutions as possible) and does not occurs in the host (Human) 2021/12/23 5

Applications 3. Creating Universal PCR Primers 4. Creating Unbiased Consensus Sequences 5. Anti-sense Drug Design 6. In coding theory (computer science) 2021/12/23 6

Distinguishing String Selection Problem Instance: Given a set B of n 1 (bad) strings of length L, a set G of n 2 (good) strings of length L, two thresholds db and dg ( db < dg). Objective: Find a string s such that for each string b B, d(s, b) db Bad strings and for any string g G, d(s, g) dg. Center string Good Strings 2021/12/23 7

Closest String Problem Instance: Given a set B of n strings of length L, and an integer d Objective: Find a string s of length L such that for each string si B, d(s, si) d Theorem: Closest string problem is NP-hard. (Lanctot, Li, Ma, Wang, Zhang, 1999) 2021/12/23 8

Closest Substring Problem Instance: Given a set B of n strings of length at least L, and an integer d Objective: Find a string s of length L such that for each string si B, there is a substring ti of si (with length L) such that d(s, si) d Theorem: Closest substring problem is NP-hard. (K. Lanctot, M. Li, B. Ma, S. Wang, and L. Zhang 1999) A PTAS was given in M. Li, B. Ma, and L. Wang 2000 2021/12/23 9

Consensus Pattern Instance: Given a set B of n strings of different lengths, and an integer L, Objective: Find a string s of length L and for each string si B, find a substring ti of si such that n i=1 d(s, ti) is minimized. Theorem: The consensus pattern problem is NP-hard. There is a PTAs for consensus pattern. (M. Li, B. Ma, and L. Wang, 1999) 2021/12/23 10

Farthest String Problem (the other half) Instance: Given a set G of n strings of length L, and an integer d Objective: Find a string s of length L such that for each string si G, d(s, si) d. Theorem: Farthest String Problem is NP-hard. (K. Lanctot, M. Li, B. Ma, S. Wang, and L. Zhang, 1999) A PTAS -- A linear programming + random rounding d is very large, i. e, O(L). (K. Lanctot, M. Li, B. Ma, S. Wang, and L. Zhang 1999) 2021/12/23 11

Computer Science Background Knowledge NP-complete Problems: unlikely to have a polynomial time algorithm to optimally solve the problem A- an approximation algorithm for a minimization problem. performance ratio: a number r such that for any instance I A(I)/OPT(I) r A(I) - the cost of the solution for instance I produced by A OPT(I) - the cost of an optimal solution for instance I. approximation scheme: an algorithm A with input I and an error bound that has the performance ratio 1+ . a family of algorithms A, one for each . 2021/12/23 12

Computer Science Background Knowledge Polynomial time approximation scheme (PTAS): an approximation scheme A that runs in time polynomial in the size of the instance I, for any fixed . MAX SNP-hard: unlikely to have a PTAS. 2021/12/23 13

Summary of our theoretical results: • Closest string problem: A PTAS (M. Li, B. Ma, and L. Wang, STOC 99) • Closest substring Problem: A PTAS (Li, Ma, Wang, 2002, JACM) Consensus pattern problem: NP-hard and A PTAS ( Li, . Ma, and Wang, JCSS, 2002) • Distinguishing string Selection Problem: PTAS • Distinguishing Substring Selection Problem: A PTAS (Deng, Li, MA and Wang, SIAM J. on Computing, 2003) 2021/12/23 14

Our Results An approximation scheme that takes an >0 as a parameter and finds a string s such that for each string b B there exists a substring t of b with length L such that d(s, t) (1+ ) db, and for any string g G, d(s, g) (1 - ) dg. 2021/12/23 15

Computation of the Closest String Problem Theorem: Closest string problem is NP-hard. (K. Lanctot, M. Li, B. Ma, S. Wang, and L. Zhang 1999) A 4/3(1+ ) approximation: (K. Lanctot, M. Li, B. Ma, S. Wang, and L. Zhang 1999) (L. Gasieniec, J. Jansson, and A. Lingas 1999) A PTAS was presented for the problem (M. Li, B. Ma, and L. Wang, 1999) 2021/12/23 16

Linear Programming Approach The optimization problem: min d; d(si, x) d, i =1, 2, … , n. 2021/12/23 17

Linear Programming Approach The optimization problem min d; a xj, a = 1, j =1, 2 , … , L ; 1 j L a (si[j], a) xj, a d, i = 1, 2, … , n. xj, a – 0 -1 variable denoting whether x[j] = a (si[j], a) – denote whether si[j] = a x'j, a – a fractional solution to the above LP 2021/12/23 18

Linear Programming Approach (continued) Randomized Rounding: with probability x'j, a , set xj, a = 1. Theorem: For any > 0, if L 4(ln n)/ 2, and d = (L), then d(si, x ) d(1+ ). 2021/12/23 When L< 4(ln n)/ 2 : enumerate all possible strings of length L. 19

when d is small (d < O(L)) Theorem: Let 1 i 1, i 2, …, ir n and Qi 1, i 2, …, ir be the set of positions where si 1, si 2, …, sir agree. There exist indices 1 i 1, i 2, …, ir n such that for any sl |{j Qi 1, i 2, …, ir | si 1[j] sl[j] and si 1[j] s[j]}| 1/(2 r-1) d, when max d(si, sj) > 1+1/(2 r-1). Note that si 1 and s can be different in many bits in Qi 1, i 2, …, ir . However, the effect on each sl B is not bad. 2021/12/23 20

The Algorithm Step 1: choose the good indices 1 i 1, i 2, …, ir n and compute Qi 1, i 2, …, ir. (Try all possible r-tuples) Step 2. Set P = {1, 2, …, L} - Qi 1, i 2, …, ir. Step 3. Use linear programming approach to solve the problem on P. (modify the inequalities a little bit. ) Step 4. Use si 1 as the solution at positions in Qi 1, i 2, …, ir. Step 5. Combine the two parts to get a string of length L. 2021/12/23 21

Old approximation algorithm for Consensus Pattern (1) Randomly select t sequences from the n given sequences. (2) Try (m-L+1)t different ways to get the occurrences of the motif in the t selected sequences. (3) Use the t substrings to form an approximate motif. (4) Use the approximate motif to search all n sequences and reconstruct the new motif based on n substrings. select t sequences 2021/12/23 22

New randomized algorithm for Consensus Pattern (Wang and Dong, 2004) (1) Randomly select k positions from the L positions (2) Try 4 k possible consensus strings of length k. (3) Use the partial consensus strings to search all the given strings and find a substring that is closest to the partial string for each of the n given strings (4) Reconstruct the center string (by choose the majority letter for each column) (5) Repeat (1)-(4) several times and choose the best output. 2021/12/23 23

Theorem: Assume d(ti, s*)=O(L). With high probability, the algorithm output a string s’ with cost n n d(t’i, s’) < (1+ ) i=1 d(ti, s*), i=1 where s* is the optimal string, t’i and ti are substrings in si that may or may not be identical. The probability is related to nm (total length of 2021/12/23 strings) and k is related to , n and m. 24

• It is expected that the algorithm might be practical since it is a random algorithm. • Theoretical results shows that k is required to be large in order to get good results. • Comparing with the best known software (Random projection algorithm + EM), the random algorithm is much slower. • We try to combine our random algorithm with EM • Exciting new findings 2021/12/23 25

A challenging instance (L, d), e. g. , (15, 4) • 20 sequences over 4 letters (randomly generated) • 600 letters in each sequence • A “Pattern” was constructed as follows: Given a center string s of length 15, we randomly change 4 positions and get 20 strings of length 4 (with 4 different letters each). • Put each of the 20 strings back to the 20 sequences of length 600 (the location is randomly chosen) • Challenge: find the inserted 20 strings 2021/12/23 26

The EM Algorithm • Input: – a 4 L weight matrix W (the initial guess of A 0. 25 0. 0 the motif); C 0. 25 1. 0 – n sequences S 1, S 2, . . . , Sn. G 0. 25 0. 0 • Output: T 0. 25 0. 0 – new W that is a local maximal solution – An array P indicating the probability that the motif starts at every position of every sequence. 2021/12/23 27

Step 1 For each position x in each sequence Si, calculate the probability that we observe this sequence data if the motif starts from position x: P(i, x)= j=1 to L W(bj, j) bj=Si(x+j) : the j-th base of the L-mer starting at x in Si. • To avoid zero weights, a fixed small number is added to W(i, j). 2021/12/23 28

Step 2 For each L-mer in each sequence, normalize the probability that this Lmer is an occurrence of the motif as: m-L+1 P'(i, x)=P(i, x) / x=1 P(i, x) and replace P with P'. Its purpose is to guarantee that x=1 to n-l+1 P'(i, x)=1. 2021/12/23 29

Step 3 Re-estimate the motif weight matrix W. W= i=1 n x=1 m-L+1 Wi, x Where Wi, x(b, j)=P(i, x) if b=Si(x+j), else 0. 2021/12/23 30

Step 4 Because the sum of each column of W should be 1. 0, a normalization is applied to W. W'(i, j)= W(i, j)/ b=a, c, g, t. W(b, j). Replace W with W'. 2021/12/23 31

Step 5 Steps 1 to 4 is called a cycle. If W changes very little from last cycle, then EM converges and the algorithm ends. Else, goto step 1 and start next cycle. How to determine the amount of change? Consider the two consecutive matrices Wq -1 and Wq. max|Wq(i, j)-Wq-1(i, j)|< 2021/12/23 32

An Example A C G T 0. 25 W 1= 2021/12/23 0. 0 1. 0 0. 0 1. 0 A p 1 C 0 G 0 T 0 s 1=ACT P 1=0. 25 1. 0 s 2=CGG P 2=0. 25 , is small, but >0. 0 p 1 0 0 0 p 1 A W 2= C G T 0 p 2 0 0 0 p 2 0 33

EM with threshold In order to accelerate the EM algorithm, a threshold is added to step 3. An L-mer takes part in the re-estimation of the motif matrix only when its likelihood P(i, x) is not less than the average likelihood of all the L-mers in this sequence. So step 3 is modified to: W= i=1 to t {Wi, x|P(i, x) 1/(n-l+1)} 2021/12/23 34

Benefits of the threshold First, each EM cycle takes less time than before, because not every Wi, x needs to be summed. Second, EM converges faster and more efficient, because the positions we neglect are more likely to be noise than to be meaningful motif occurrences. The average number of cycles changes from 6. 0 to less than 4. And the probability that EM finds the correct motif becomes larger. 2021/12/23 35

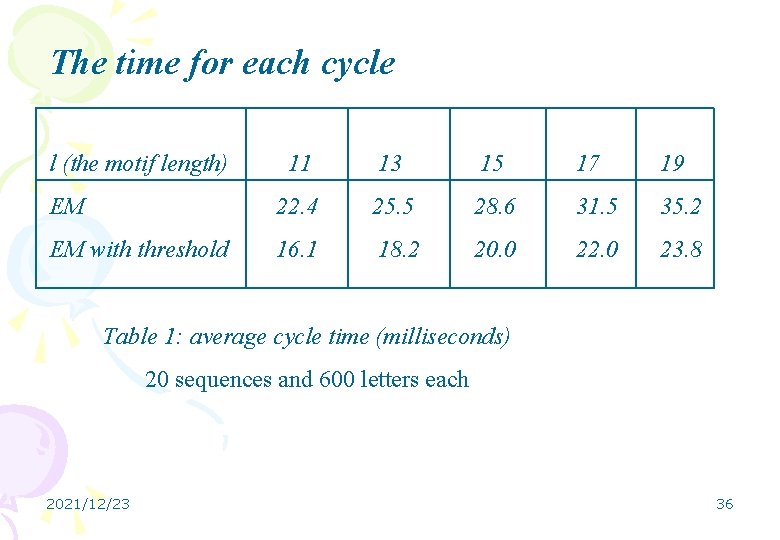
The time for each cycle l (the motif length) 11 13 15 17 19 EM 22. 4 25. 5 28. 6 31. 5 35. 2 EM with threshold 16. 1 18. 2 20. 0 22. 0 23. 8 Table 1: average cycle time (milliseconds) 20 sequences and 600 letters each 2021/12/23 36

The Whole Algorithm 1 for trial=1 to m do 2 choose k positions from L positions randomly; 3 generate 4 k starting points; 4 for i=1 to 4 k do 5 refine the i-th starting point; 6 if an (L, d) motif is found (error <=d) then goto 7; 72021/12/23 report the best motif ever found. 37

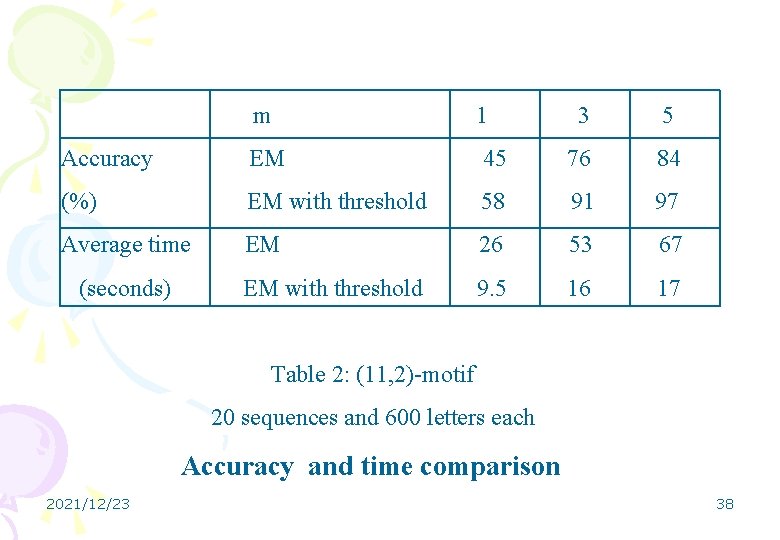
m 1 Accuracy EM (%) Average time (seconds) 3 5 45 76 84 EM with threshold 58 91 97 EM 26 53 67 EM with threshold 9. 5 16 17 Table 2: (11, 2)-motif 20 sequences and 600 letters each Accuracy and time comparison 2021/12/23 38

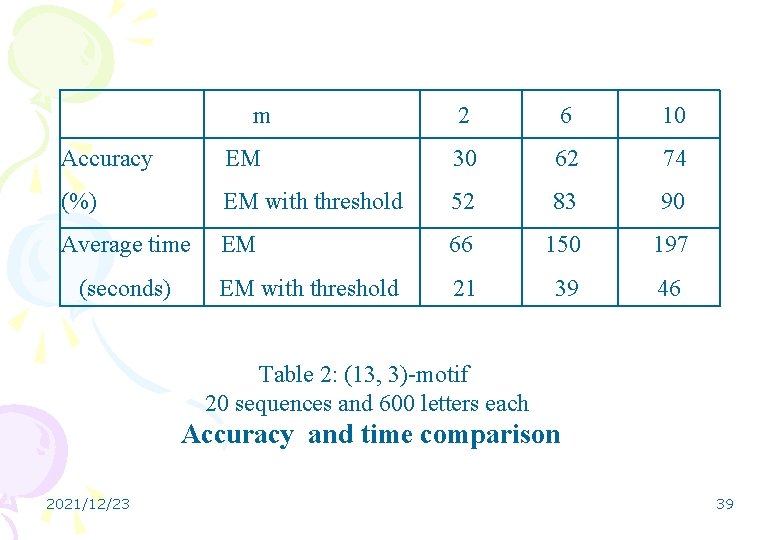
m 2 6 10 Accuracy EM 30 62 74 (%) EM with threshold 52 83 90 Average time EM 66 150 197 EM with threshold 21 39 46 (seconds) Table 2: (13, 3)-motif 20 sequences and 600 letters each Accuracy and time comparison 2021/12/23 39

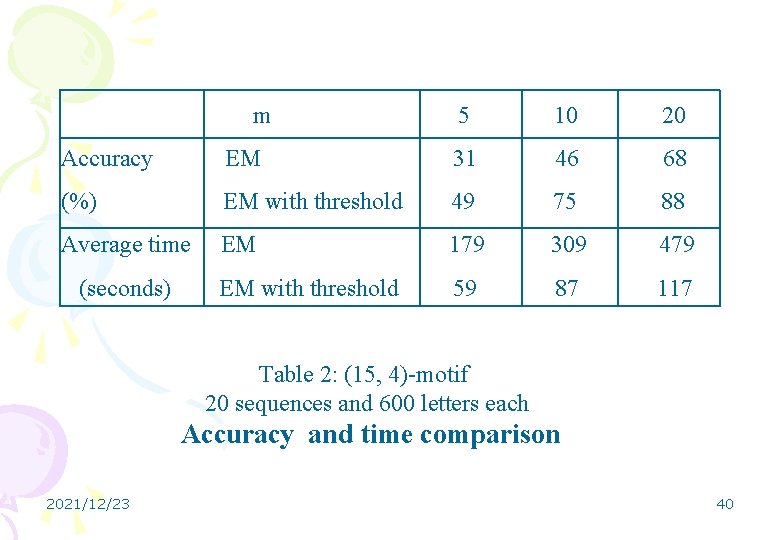
m 5 10 20 Accuracy EM 31 46 68 (%) EM with threshold 49 75 88 Average time EM 179 309 479 EM with threshold 59 87 117 (seconds) Table 2: (15, 4)-motif 20 sequences and 600 letters each Accuracy and time comparison 2021/12/23 40

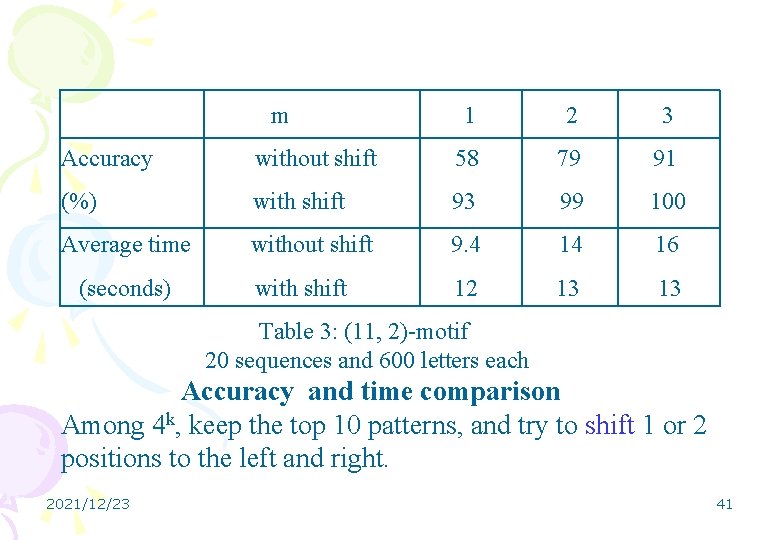
m 1 2 3 Accuracy without shift 58 79 91 (%) with shift 93 99 100 Average time without shift 9. 4 14 16 with shift 12 13 13 (seconds) Table 3: (11, 2)-motif 20 sequences and 600 letters each Accuracy and time comparison Among 4 k, keep the top 10 patterns, and try to shift 1 or 2 positions to the left and right. 2021/12/23 41

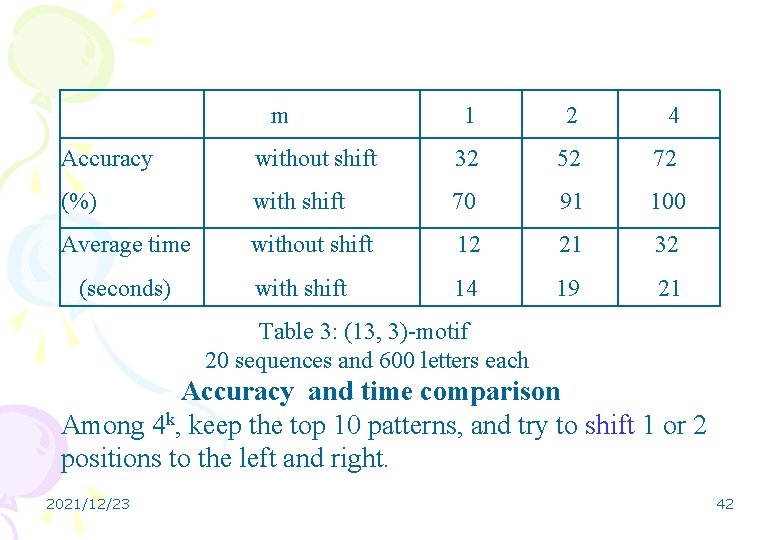
m 1 2 4 Accuracy without shift 32 52 72 (%) with shift 70 91 100 Average time without shift 12 21 32 with shift 14 19 21 (seconds) Table 3: (13, 3)-motif 20 sequences and 600 letters each Accuracy and time comparison Among 4 k, keep the top 10 patterns, and try to shift 1 or 2 positions to the left and right. 2021/12/23 42

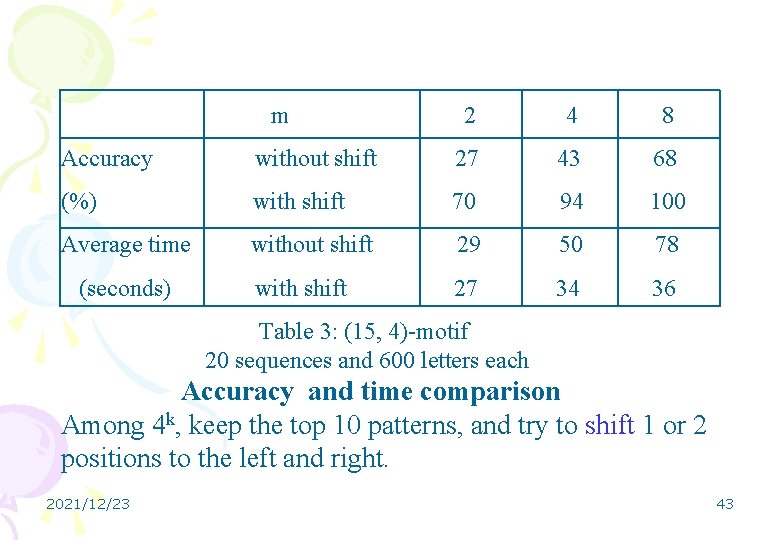
m 2 4 8 Accuracy without shift 27 43 68 (%) with shift 70 94 100 Average time without shift 29 50 78 with shift 27 34 36 (seconds) Table 3: (15, 4)-motif 20 sequences and 600 letters each Accuracy and time comparison Among 4 k, keep the top 10 patterns, and try to shift 1 or 2 positions to the left and right. 2021/12/23 43

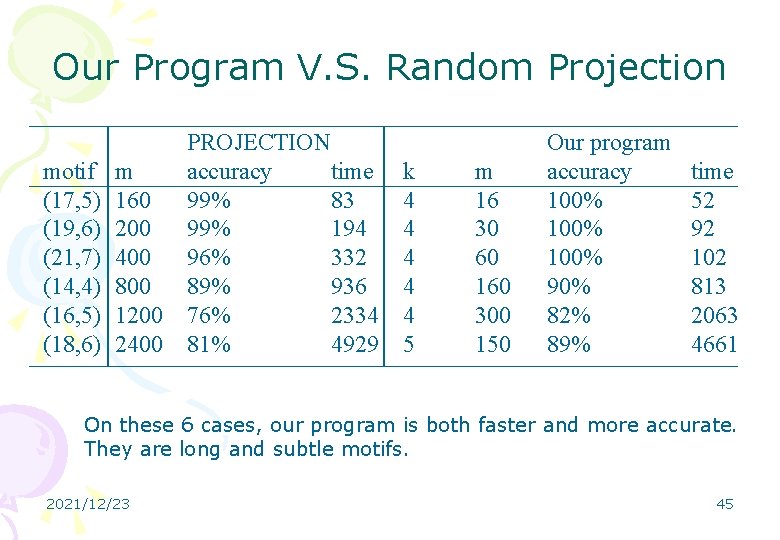
Our Program V. S. Random Projection motif (9, 1) (8, 1) (11, 2) (13, 3) (15, 4) (10, 2) (12, 3) m 1 3 6 12 30 60 300 PROJECTION accuracy time 100% 4. 3 100% 5. 6 100% 12 100% 26 100% 25 99% 203 k 4 4 4 4 m 1 5 3 4 8 30 70 Our program accuracy 100% 100% 99% time 6. 9 9. 6 13 21 36 47 207 On these 7 cases, PROJECTION (Buhler and Tompa, 2002) runs faster than our program. They are short and easy motifs. 2021/12/23 44

Our Program V. S. Random Projection motif (17, 5) (19, 6) (21, 7) (14, 4) (16, 5) (18, 6) m 160 200 400 800 1200 2400 PROJECTION accuracy time 99% 83 99% 194 96% 332 89% 936 76% 2334 81% 4929 k 4 4 4 5 m 16 30 60 160 300 150 Our program accuracy 100% 90% 82% 89% time 52 92 102 813 2063 4661 On these 6 cases, our program is both faster and more accurate. They are long and subtle motifs. 2021/12/23 45

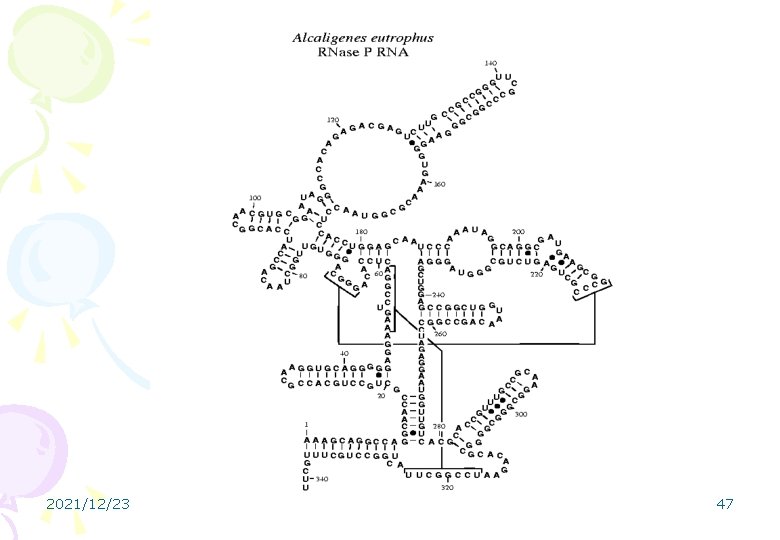
Parametric Alignment of RNA secondary structures(L. Wang, J. Zhao, H. Zhao) • RNA secondary structures can be decomposed into five types of components: • Stem, hairpin, bulge, interior loop and multibranch loop. • An ordered tree can be used to describe RNA secondary structures • The order among siblings in the tree is important. 2021/12/23 46

2021/12/23 47

Comparison of ordered trees • Alignment of trees: • Operations: insertion, deletion, match and mismatch. • Parameters: cost for (1) insertion/deletion, (2) gap penalty, and (3) mismatch (cost of match is fixed as 1. ) Setting of parameters is important http: //www. cs. cityu. edu. hk/~lwang/software/Para. Tree/index. html 2021/12/23 48

Direct comparison of RNA secondary structures • Measures have been proposed to directly compare two RNA secondary structures. (Zhang et al, 2000) O(|P 1|x|P 2|x|R 1|x|R 2|). • We are working on a software (parametric version). 2021/12/23 49

The algorithm for aligning two RNA structures 2. Secondary Structure: a sequence with noncrossing base pairs ACGUGGACCGC 3. Tertiary Structure: a sequence with crossing base pairs. AGUGGUCUCUAGCU • one base in at most one pair 2021/12/23 50

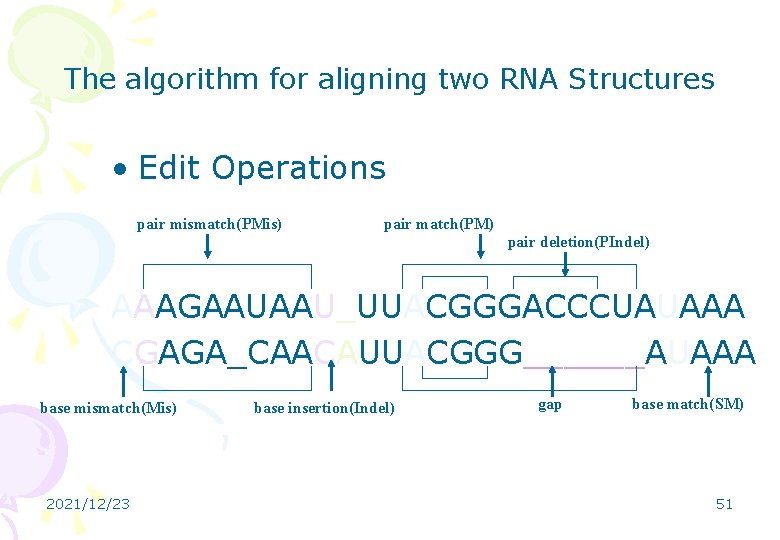
The algorithm for aligning two RNA Structures • Edit Operations pair mismatch(PMis) pair match(PM) pair deletion(PIndel) AAAGAAUAAU_UUACGGGACCCUAUAAA CGAGA_CAACAUUACGGG______AUAAA base mismatch(Mis) 2021/12/23 base insertion(Indel) gap base match(SM) 51

The algorithm for aligning two RNA Structures Definition: Alignment between R 1 and R 2 • R 1 insert “_”, R 2 insert “_”. | |=| | AAAG AUAG • A_AAG AU_AG single base aligned to single base or “_”. AAAGUC AAUUC 2021/12/23 AAAGUC AA_UUC 52

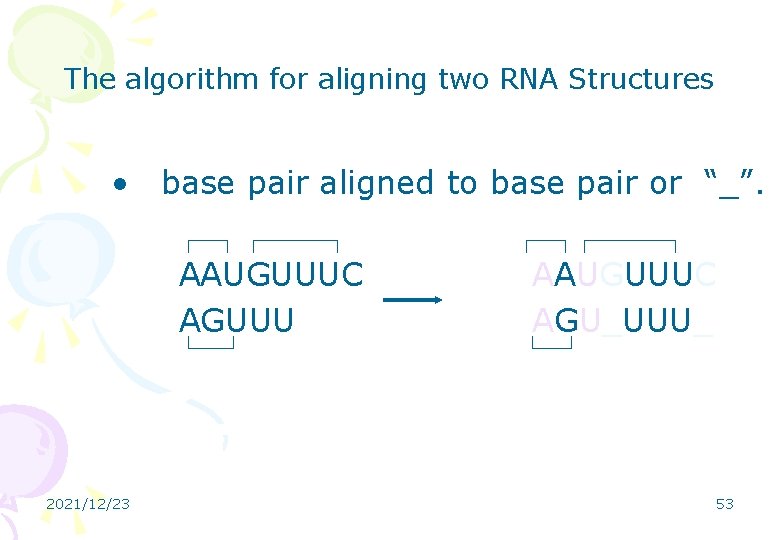
The algorithm for aligning two RNA Structures • base pair aligned to base pair or “_”. AAUGUUUC AGUUU 2021/12/23 AAUGUUUC AGU_UUU_ 53

Computation of signed translocation distance Chromosome: a set of genes in a linear order. Gemone: a set of chormosomes. Example: A={ (1, 2, 3, 4, 5, 6, 7, -8, 9, 10, 11, -12), (13, 14, 15, 16, 17)} 2021/12/23 54

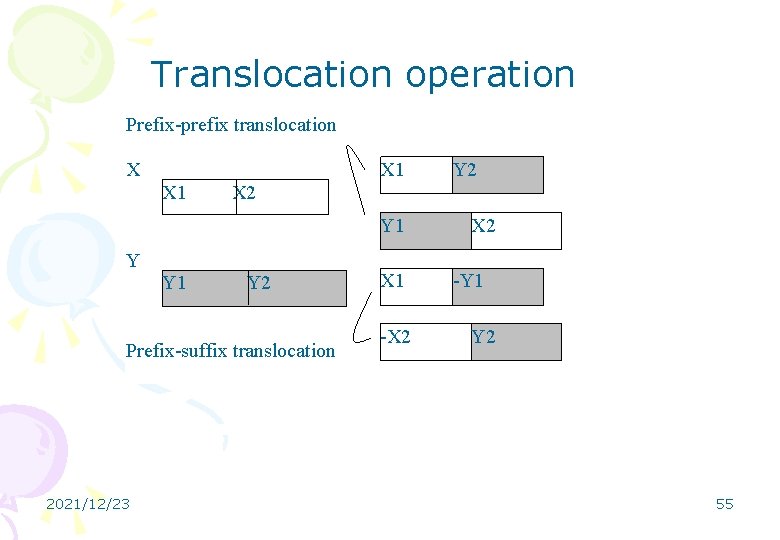
Translocation operation Prefix-prefix translocation X X 1 X 2 Y 1 Y 2 Prefix-suffix translocation 2021/12/23 Y 2 X 1 -X 2 -Y 1 Y 2 55

Translocation distance: the minimum number of translocations required to transform one genome into another. Computing the distance: given two signed genomes, compute the translocation distance. Previous results: (for signed case) • O(n 3) algorithm. (Hannenhalli, 1996) • O(n 2 log n) algorithm. (Zhu, 2001) 2021/12/23 56

Our results: (with Zhu and Liu) • O(n 2) algorithm for signed case • NP-hard for unsigned case. (settled an main open problem) (in preparation with Zhu, et al. ) • A software is produced. (with Feng, 2004) • http: //www. cs. cityu. edu. hk/~lwang/so ftware/Translocation/index. html 2021/12/23 57

Open Problem(8 years old) • Transposition: Chromosome: X=X 1 X 2. . . Xi…Xj…. Xk+1…Xn. After operation: Chromosome: X 1 X 2…Xi-1 Xj+1…Xk. Xi…Xj. Xk+1…Xn. Is there any polynomial time algorithm? 2021/12/23 58