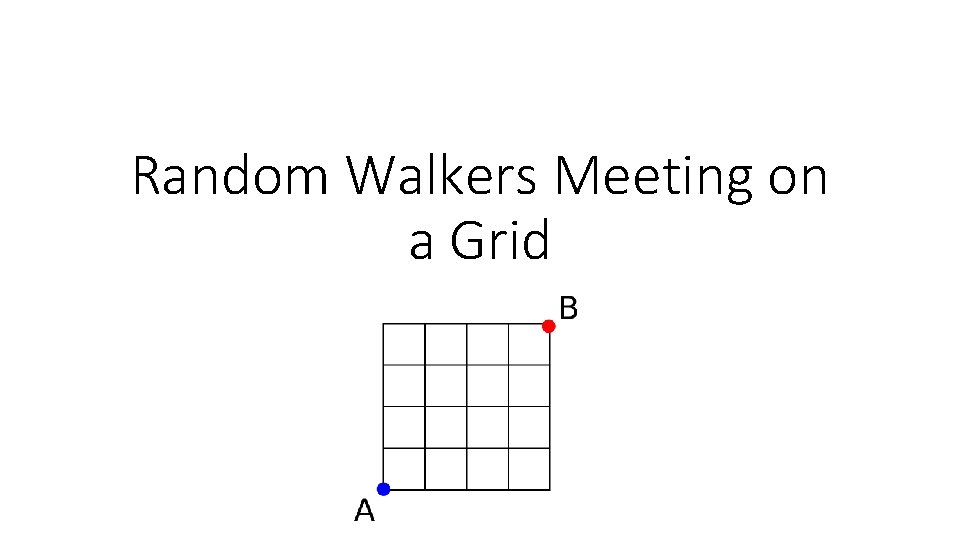
Random Walkers Meeting on a Grid Random walkers



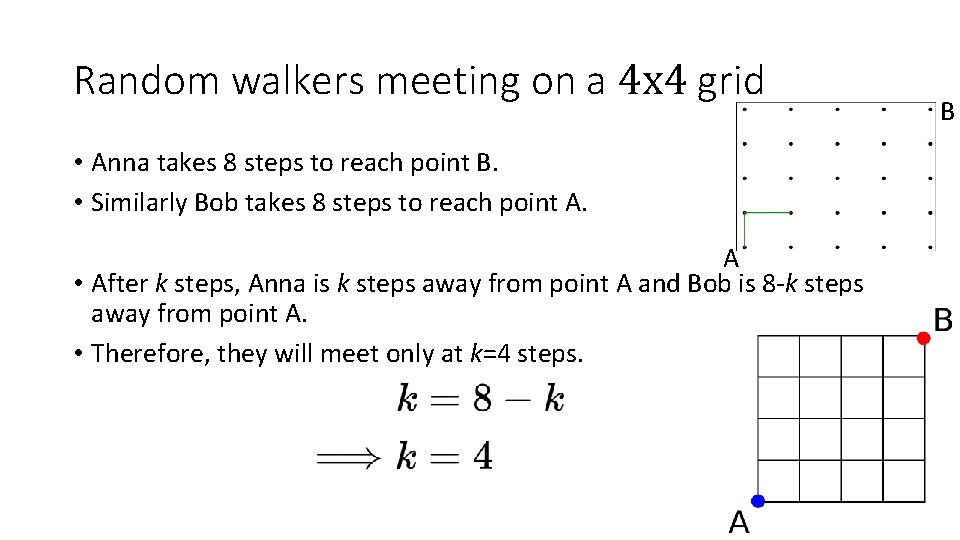
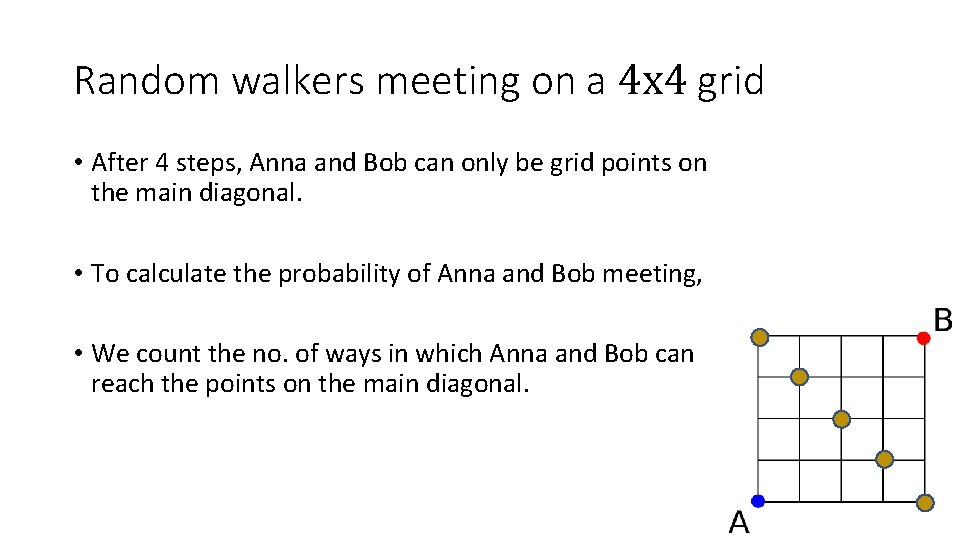
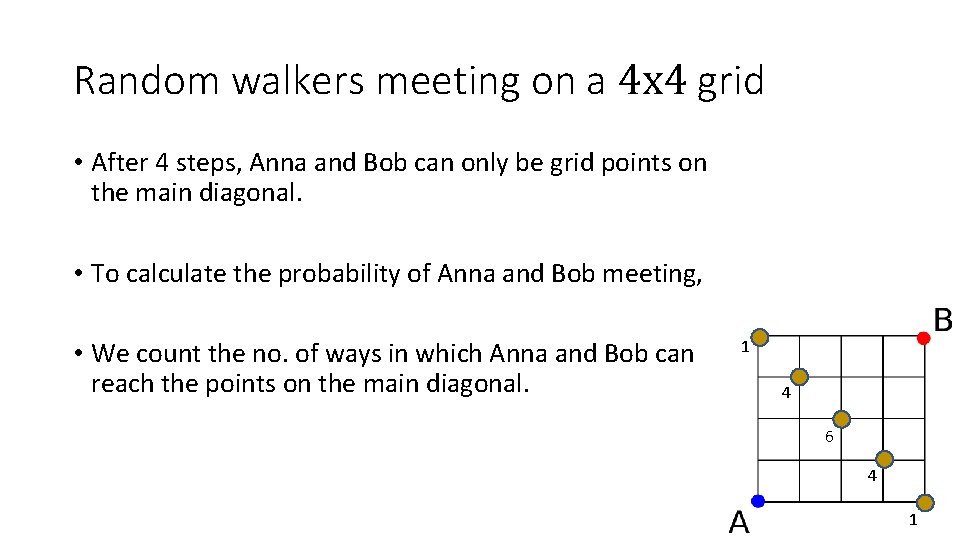
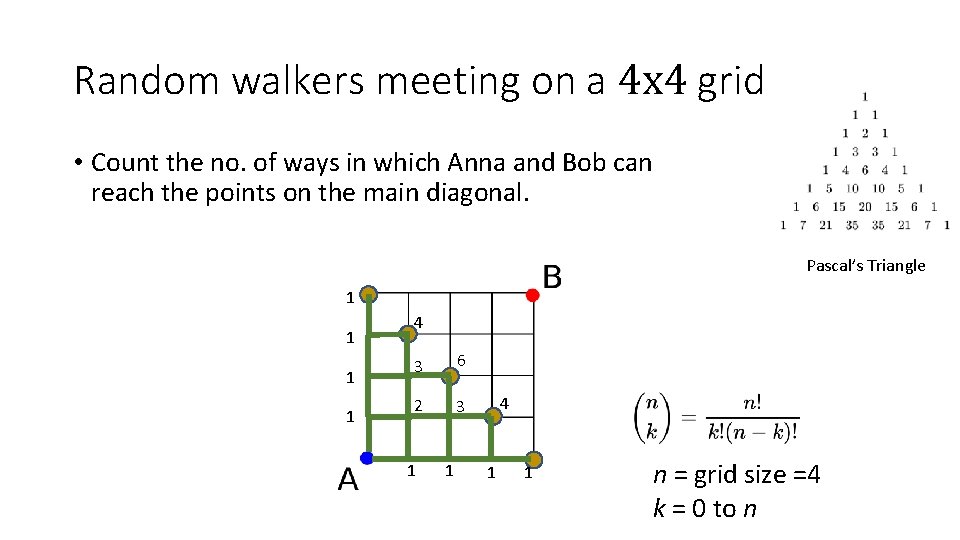
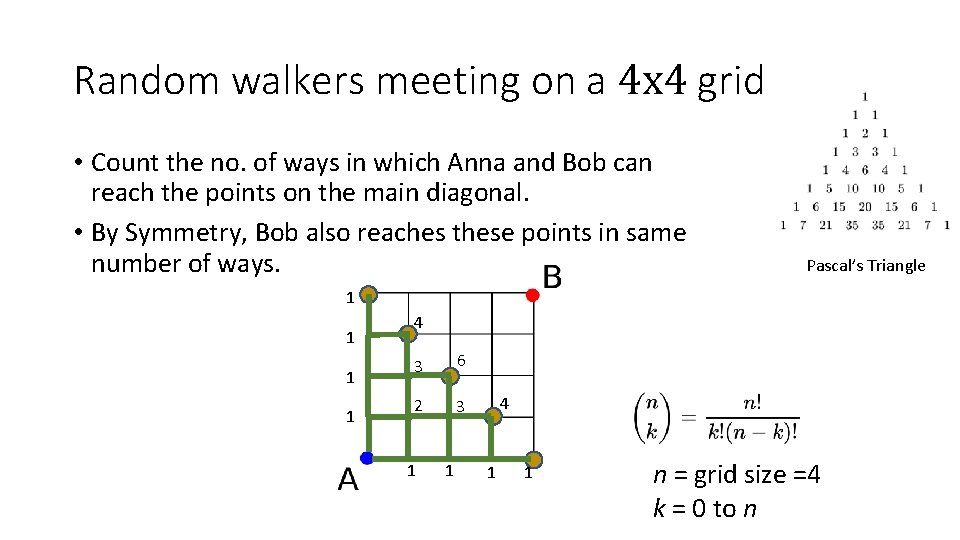



- Slides: 14

Random Walkers Meeting on a Grid

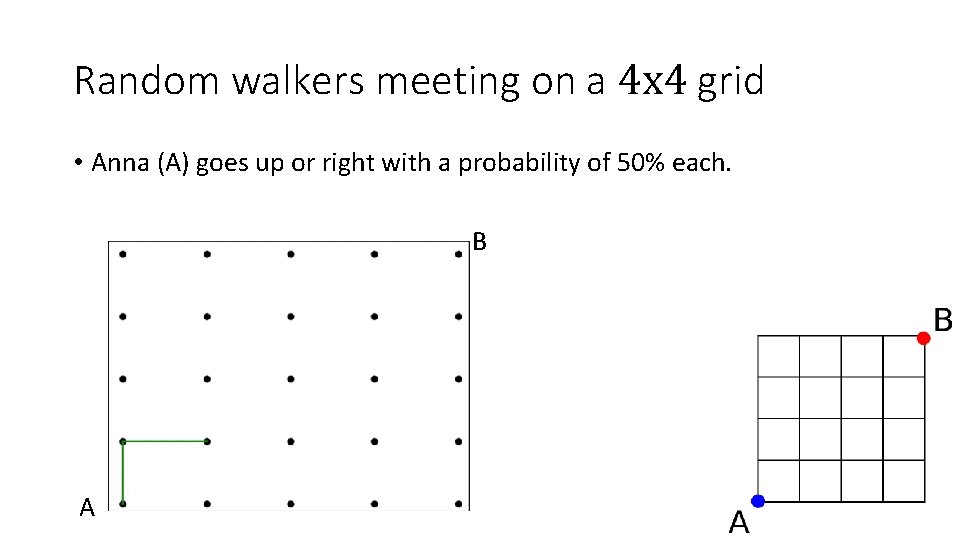
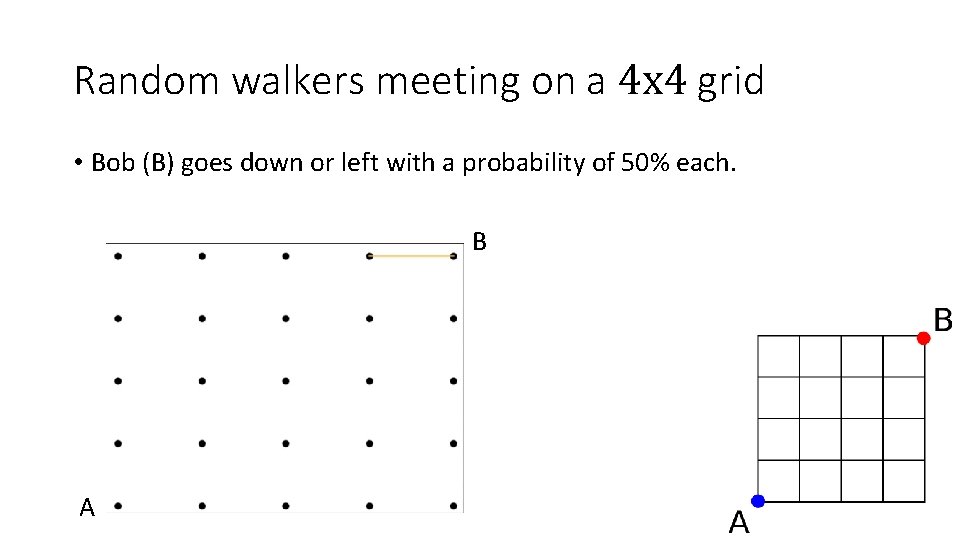
Random walkers meeting on a 4 x 4 grid • Anna (A) goes up or right with a probability of 50% each. • Bob (B) goes down or left with a probability of 50% each. • What is the probability of the protagonists meeting each other?

Random walkers meeting on a 4 x 4 grid • Anna (A) goes up or right with a probability of 50% each. B A

Random walkers meeting on a 4 x 4 grid • Bob (B) goes down or left with a probability of 50% each. B A

Random walkers meeting on a 4 x 4 grid • Anna (A) goes up or right with a probability of 50% each. • Bob (B) goes down or left with a probability of 50% each. • What is the probability of the protagonists meeting each B other?

Random walkers meeting on a 4 x 4 grid After how many steps is it possible for the protagonsits to meet? B A Possible to meet after 4 steps (Not guaranteed)
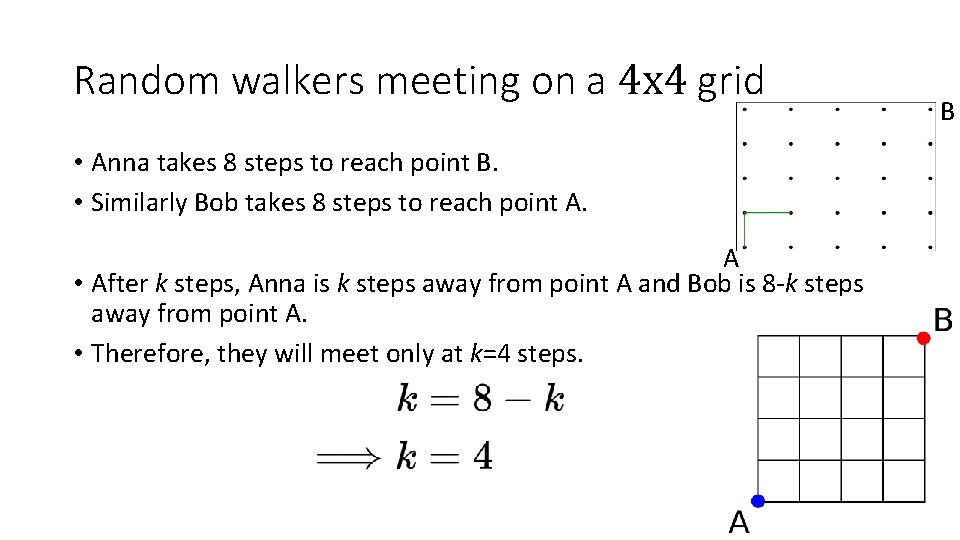
Random walkers meeting on a 4 x 4 grid • Anna takes 8 steps to reach point B. • Similarly Bob takes 8 steps to reach point A. A • After k steps, Anna is k steps away from point A and Bob is 8 -k steps away from point A. • Therefore, they will meet only at k=4 steps. B
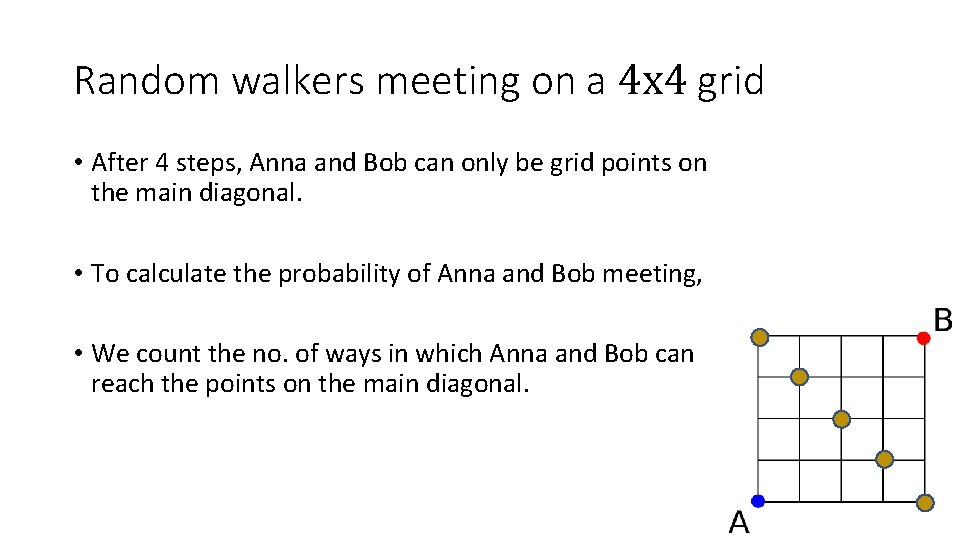
Random walkers meeting on a 4 x 4 grid • After 4 steps, Anna and Bob can only be grid points on the main diagonal. • To calculate the probability of Anna and Bob meeting, • We count the no. of ways in which Anna and Bob can reach the points on the main diagonal.
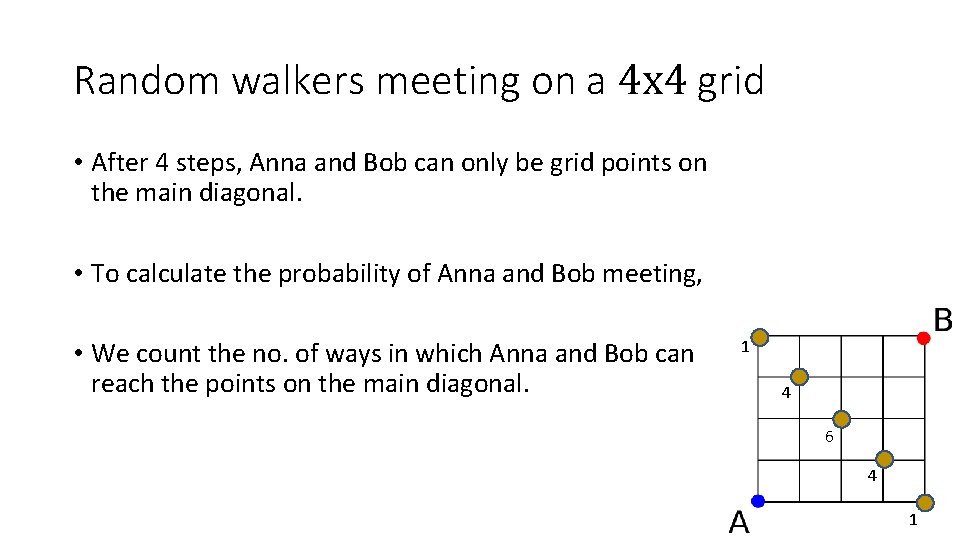
Random walkers meeting on a 4 x 4 grid • After 4 steps, Anna and Bob can only be grid points on the main diagonal. • To calculate the probability of Anna and Bob meeting, • We count the no. of ways in which Anna and Bob can reach the points on the main diagonal. 1 4 6 4 1
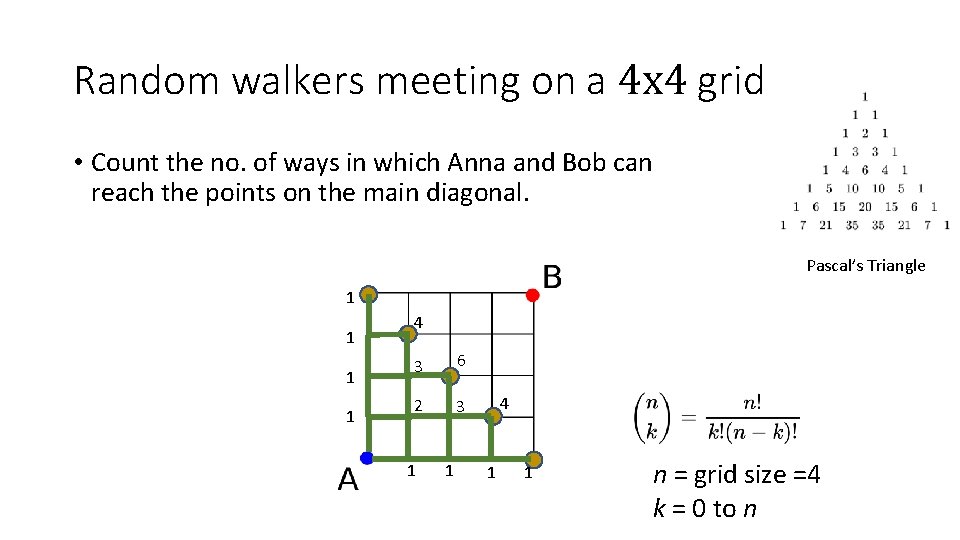
Random walkers meeting on a 4 x 4 grid • Count the no. of ways in which Anna and Bob can reach the points on the main diagonal. Pascal’s Triangle 1 1 4 3 6 2 3 1 1 4 1 1 n = grid size =4 k = 0 to n
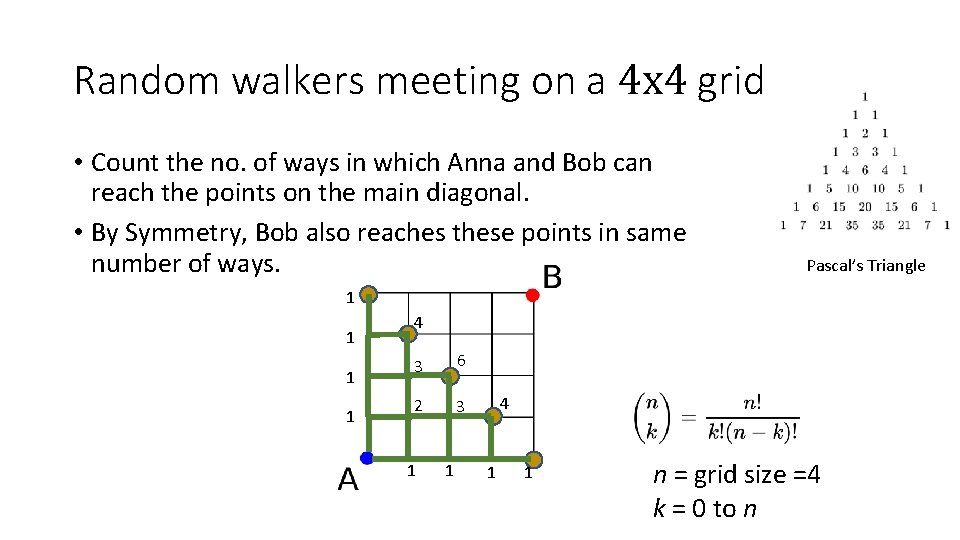
Random walkers meeting on a 4 x 4 grid • Count the no. of ways in which Anna and Bob can reach the points on the main diagonal. • By Symmetry, Bob also reaches these points in same number of ways. Pascal’s Triangle 1 1 4 3 6 2 3 1 1 4 1 1 n = grid size =4 k = 0 to n

Random walkers meeting on a 4 x 4 grid • 1 4 6 4 1

Random walkers meeting on a 4 x 4 grid • 1 4 6 4 1

Random walkers meeting on a nxn grid