Random Walk on Graphs and its Algorithmic Applications

Random Walk on Graphs and its Algorithmic Applications Shengyu Zhang Winter School, ITCSC@CUHK, 2009

Random walk on graphs On an undirected graph G: n Starting from vertex v 0 n Repeat for a number of steps: q n Go to a random neighbor. Simple but powerful.

Road map: Random walk Parameters /Properties Algorithms Hitting time q k SAT q st connectivity Mixing time q Page. Rank q Approximate counting q Error reduction

Road map: Quantum walk Short intro to math model of quantum mechanics Types Algorithms Discrete QW Element Distinctness Continuous QW Formula Evaluation

PART I. Random Walk Key parameter 1: Hitting time

Hitting time n Recall the process of random walk on a graph G. q q Starting vertex v 0 Repeat for a number of steps: n j Go to a random neighbor. i n Hitting time: H(i, j) = expected time to visit j (for the first time), starting at i

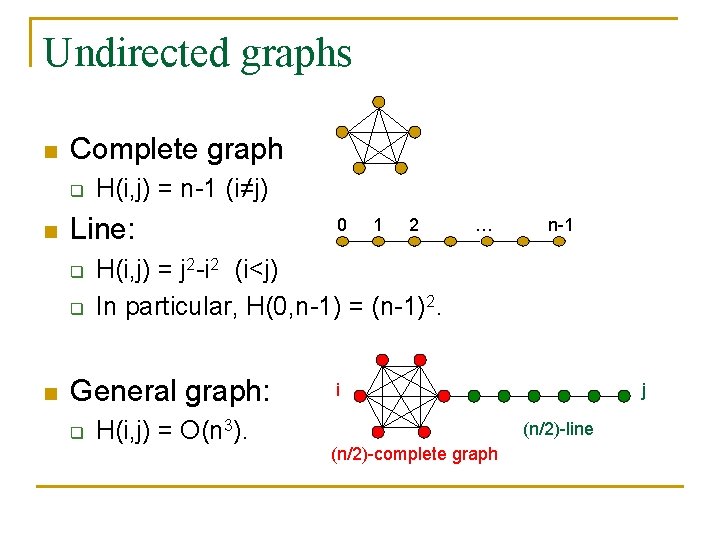
Undirected graphs n Complete graph q n Line: q q n H(i, j) = n 1 (i≠j) 1 2 … n 1 H(i, j) = j 2 i 2 (i<j) In particular, H(0, n 1) = (n 1)2. General graph: q 0 H(i, j) = O(n 3). i j (n/2) line (n/2) complete graph

Algorithm 1: 2 -SAT

k-SAT: satisfiability of k-CNF formula n n n variables x 1, …, xn∊{0, 1} m clauses, each being OR of k literals q q n n Literal: xi or ¬xi e. g. (k=3): (¬x 1) ٧ x 5 ٧ x 7 3 CNF formula: AND of these m clauses q e. g. ((¬x 1) ٧ x 5 ٧ x 7) ٨ (x 2 ٧ (¬x 5) ٧ (¬x 7)) ٨ (x 1 ٧ x 7 ٧ x 8) 3 -SAT Problem: Given a 3 CNF formula, decide whethere is an assignment of variables s. t. the formula evaluates to 1. q For the above example, Yes: x 5=1, x 7=0, x 1=1

P vs. NP n P: problems that can be easily solved q n “easily”: in polynomial time NP: problems that can be easily verified. q Formally: ∃ a polynomial time verifier V, s. t. for any input x, n n n If the answer is YES, then ∃y s. t. V(x, y) = 1 If the answer is NO, then ∀y, V(x, y) = 1 The question of TCS: Is P = NP? q Intuitively, no. NP should be much larger. n n q It’s much easier to verify (with help) than to solve (by yourself) mathematical proof, appreciation of good music/food, … Formal proof? We don’t know yet. n One of the 7 Millennium Problems by CMI. ① ① http: //www. claymath. org/millennium/P_vs_NP/

NP-completeness n n k SAT is NP complete, for any k ≥ 3. NP complete: q q n n NP complete problems are the hardest ones in NP. 3 SAT is in NP: q q n In NP All other problems in NP can be reduced to it in poly. time witness satisfying assignment A Verification: evaluate formula with variables assigned by A [Cook Levin] 3 SAT is NP complete.

How about 2 -SAT? n While 3 SAT is the hardest in NP, 2 SAT is solvable in polynomial time. n Here we present a very simple randomized algorithm, which has polynomial expected running time.

Algorithm for 2 -SAT n 2 SAT: each clause has two variables/negations (x 1∨x 2)∧(x 2∨¬x 3) ∧(¬x 4∨x 3) ∧(x 5∨x 1) n Alg [Papadimitriou]: q q Pick any assignment Repeat O(n 2) time n n If all satisfied, done Else q q x 1, x 2, x 3, x 4, x 5 0, 1, 0 1 Pick any unsatisfied clause Pick one of the two literals each with ½ probability, and flip the assignment on that variable

Analysis n (x 1∨x 2)∧(x 2∨¬x 3) ∧(¬x 4∨x 3) ∧(x 5∨x 1) q q n n x 1, x 2, x 3, x 4, x 5 0, 1, 0 If unsatisfiable: never find an satisfying assignment If satisfiable, there exists a satisfying assignment x q q q If our initially picked assignment x’ is satisfying, then done. Otherwise, for any unsatisfied clause, at least one of the two variables is assigned a value different than that in x Randomly picking one of the two variables and flipping its value increases # correct assignments by 1 w. p. ≥ ½

Analysis (continued) n Consider a line of n+1 points, where k represents “we’ve assigned k variables correctly” q n n Last slide: Randomly picking one of the two variables and flipping its value increases # correct assignments by 1 w. p. ≥ ½ Thus the algorithm is actually a random walk on the line of n+1 points, with Pr[going right] ≥ ½. q n “correctly”: the same way as x Hitting time (i → n): O(n 2) So by repeating this flipping process O(n 2) steps, we’ll reach x with high probability.

Algorithm 2: st-connectivity

st-Connectivity n Problem: Given a graph G and two vertices s and t on it, decide whether they are connected. n BFS/DFS (starting at s) solves the problem in linear time. But uses linear space as well. Question: Can we use much less space? n n

Simple random walk algorithm n A randomized algorithm takes O(log n) space. q q n Starting at s, perform the random walk for O(n 3) steps. If ever see t, output YES and stop. output NO. Why it works? H(s, t) = O(n 3). q If s can reach t, then we should see it within O(n 3) time.

Key parameter 2: Mixing time

Convergence n n Now let’s study the probability distribution of v the particle after a long time. u w What do we observe? q q n The distribution converges to uniform… wherever it starts. Q: Does this hold in general? t 0 1 1/2 0 1/2 2 1/4 2/4 1/4 3 3/8 2/8 3/8 4 5/16 6/16 5 11/32 10/32 11/32 6 21/64 22/64 21/64

Convergence v 1 n n Well, Yes and No. Consider the following cases q n n n on undirected graphs. v 2 v 3 v 4 v 5 v 1 v 2 3 4 5 6 Case 1: The graph is unconnected. v v Case 2: The graph is bipartite. [Thm] For any connected non bipartite graph, and any starting point, the random walk converges.

Converges to what? v u n n n w In the previous triangle example: uniform. In general? As a result of the convergence, the distribution doesn’t change by the matrix q If the particle is on the graph according to the distribution, then further random walk will result in the same distribution. n q We call it the stationary distribution. [Fact] It’s unique.

stationary distribution n [Fact] It’s the following distribution: π(v) = d(v)/2 m q q n n d(v) = degree of v, i. e. # of neighbors. m: |E|, i. e. # of edges. [Proof] Consider one step of walk: π’(v) = ∑u: (u, v)∊E p(u)∙[1/d(u)] = ∑u: (u, v)∊E [d(u)/2 m]∙[1/d(u)] = ∑u: (u, v)∊E 1/2 m = d(v)/2 m = π(v) So π is the stationary distribution. For regular graphs, π is the uniform distribution.

Proportional to degree n n n Note: the stationary distribution π(v) = d(v)/2 m is proportional to the degree of v. What’s the intuition? The more neighbors you have, the more chance you’ll be reached. We will see another natural interpretation shortly.

Speed of the convergence n n We’ve seen that random walk converges to the stationary distribution. Next question: how fast is the convergence? Let’s define the mixing time as min {T: ∥pi(T) - π∥ ≤ ε} where pi(T): the distribution in time T, starting at i. ∥∙∥: some norm. We’ll see the reason of mixing later. Now let’s first see an example you run into everyday.

Algorithm 3: Page. Rank

Page. Rank n Google gives each webpage a number for its “importance”. q q n [IT] Google: 10, Microsoft: 9, Apple: 9 [Media] NYTimes: 9, CNN: 10, sohu: 8, newsmth: 7 [Sports] NBA: 7, CFA: 7 [University] MIT: 9, CUHK: 8, … … Tsinghua, Pku, Fudan, IIT(B): 9 When you search for something by making a query, a large number of related webpages are retrieved. q What webpages to retrieve? Information Retrieval. That’s an orthogonal issue.

Ranking n n How to give this big corpus to you? Search engines rank them based on the “importance”, and give them in descending order. q n n Thus presumably the first page contains the 10 most important webpages related to your query. Question: How to rank? Page. Rank: Use the vast link structure as in indicator of an individual page’s value.

Reference system n Webpage A has a link to webpage B A thinks B is useful. q n So a webpage with a lot of other pages pointing to it is probably important. q n A guy getting a lot of letters is strong. Further, pointers from pages that are themselves important bear more weight. q n Think of it as A writing a recommendation letter for B. Letters by Noga, László, Sasha, Avi, Andy, … mean a lot. But the importance of those pages also need to be calculated… we have a recurrence equation.

Furthermore n If page A has a lot of links, then each link means less. q n n Ok, you get Einstein’s letter, but you know what, last year everyone on the market got his letter. So let’s assume that page A’s reference weight is divided evenly to all pages B that A links to. Recurrence equation: R(A) = ∑B: B→A R(B)/d(B) where d(B) = # pages C that B links to

Sink issue n n R(A) = ∑B: B→A R(B)/d(B) has a problem. There are some “sink” pages that contain no links to other pages. q q n Sinks accumulate weights without giving out. The recurrence equation only has solutions with weight on sinks, losing the original intension of indicating the importance of all pages. To handle this, we modify the recursion: R(A) = (1 α)/N + α ∑B: B→A R(B)/d(B) q q q Force each page to have a (1 α) fraction of weights (evenly) going to all pages. So each A also receives a weight of (1 α)/N from all pages α: around 0. 85

Random Walk view n Note that the recursion R(A) = (1 α)/N + α ∑B: B→A R(B)/d(B) is exactly the random walk on the graph, where at each point A, we q q n w/ prob. α, follow a random link; w/ prob. (1 α), go to a random page. Question: How to solve this recurrence equation? q # webpages: ~ 30 billion (and counting…)

Algorithm n Recall: the random walk converges to the stationary distribution! q n Algorithm: start from any distribution, run a few iterations of random walk, and output the result. q n It’s a bit different since it’s random walk on directed graphs, but this Page. Rank matrix has all good properties we need so that the random walk also converges to the solution. Google: 50 100 iterations, need a few days. That should be close to the stationary distribution, which serves as indictor of the importance of pages.

Next n We’ll see a bit math behind the mixing story.

Mathematics behind the mixing n [Eigenvalue decomposition] A symmetric matrix MN N can be written as M = ∑i=1, …, n λiξiξi. T q q n The eigenvectors are orthonormal. q q n n λi: eigenvalue. Order them: |λ 1| ≥ |λ 2| ≥ |λ 3| ≥ … ≥ |λn| ξi: (column) eigenvector, i. e. Mξi = λiξi ∥ξi∥ 2=1 ξi, ξj = 0, for all i≠j M 2 = (∑i=1, …, n λiξiξi. T)(∑j=1, …, n λjξjξj. T) = ∑i, j λiξiξi. T λjξjξj. T = ∑i, j λi λj ξi, ξi ξjξj. T = ∑i λi 2 ξjξi. T Mt = ∑i λit ξjξi. T

Random walk in matrix form n n A: adjacency matrix. (Aij = 1 if (i, j) ∊E; 0 o. w. ) P: probability transition matrix. q q q n N = D 1/2 AD 1/2 = D 1/2 PD 1/2 q q n Pij = 1/di if (i, j) ∊E; 0 o. w. P = D-1 A, where D = diag(d 1, …, dn). (di: deg(i)) For any distribution p, PTp is the distribution after one step of random walk Nij = 1/(didj)1/2 if (i, j) ∊E; 0 o. w. N is symmetric, so N can be written as N = ∑i=1, …, n λiξiξi. T Random Walk for t steps: q Pt = (D 1/2 ND 1/2)t = D 1/2 Nt. D 1/2 = D 1/2 (∑iλitξiξi. T)D 1/2 = ∑iλit. D 1/2ξiξi. TD 1/2

Why mixing? Why to π? n [Thm] For connected non bipartite graph, N has q q n n λ 1 = 1 and ξ 1 = π1/2 = ((d 1/2 m)1/2, …, (dn/2 m)1/2) is the square root version of the stationary distribution (so that the l 2 norm is 1). |λ 2| < 1. (So is all other λi’s. ) Random Walk for t steps: Pt = ∑i λit. D 1/2ξiξi. TD 1/2 First item: λ 1 t. D 1/2ξ 1ξ 1 TD 1/2 = D 1/2(1/2 m)[(didj)1/2]ij. D 1/2= (1/2 m)[dj]ij q For any starting distribution p, (1/2 m)[dj]ij. T p = π.

Speed of the convergence n All other items: since |λi|<1, λit. D 1/2ξiξi. TD 1/2→ 0! q Speed of convergence depends on how close |λ 2| is to 1. n Page. Rank matrix: |λ 2| = α (≈ 0. 85) n Expander: 1 |λ 2| = Ω(1)

The rest of the talk n Only ideas are given. n Many details are omitted. n I may cheat a bit to illustrate the main steps.

Algorithm 4: Approximately counting

Algorithm 4: Approximately counting n Task: estimate the size of an exponentially large set V q n Approach: find a chain V 0⊆V 1⊆…⊆Vm=V q q q n n Example: Given G, count # of perfect matchings. |V 0| is easy to compute; m = poly(n) layers; Each ratio |Vi+1|/|Vi| = poly(n) is easy to estimate. Then |V| = |V 0| (|V 1|/|V 0|) (|V 2|/|V 1|)… (|Vn|/|Vn 1|) can be estimated. Question: How to estimate |Vi+1|/|Vi|?

Estimate the ratio n Estimate by random sampling: q q n Generate a random element uniformly distributed in Vi+1, see how often it hits Vi. Question: How to uniformly sample Vi+1? By random walk q q q We construct a regular graph with vertex set Vi+1 The algorithm runs efficiently (i. e. in poly(n) time) if the walk converges to uniform rapidly (i. e. in poly(n) time). It’s the case in perfect matching counting problem.

Algorithm 5: Error Reduction with efficient randomness

Error reduction n Task: Reduce the error of a randomized algorithm A. q n q q n n → ε? Naïve approach: q n Error: Prr∈{0, 1}^m[r is bad for A] = 1/3 Draw k random strings r 1, …, rk, Run algorithm A using r 1, …, rk and get k answers Output the majority of the answers B {0, 1}m [Fact] the error drops to 2 Θ(k). Chernoff’s bound Randomness complexity: mk. Question: Can we reduce the error prob w/o using too many additional random bits?

Expander graph n Expander: Eigenvalue gap is large Ω(1) q q n Random walk converges very fast O(log n). Highly connected diameter O(log n) Large boundary any subset has lots of edges going out Could be sparse ∃ constant degree expanders. We know how to construct them explicitly.

Algorithm for error reduction n New Algorithm A’: q q q n n Thm: the error prob of A’ is also 2 Θ(k) How many random bits used? m + O(k) q n B Construct an expander with V = {0, 1}m Start from a random vertex r 1 Perform a random walk (r 1, r 2, …, rk) of length k Random algorithm A using r 1, r 2, …, rk and get k answers Output the majority of the answers The expander is of constant degree. Highly dependent! Why it works?

Expander: large boundary n For simplicity, consider the one side error case: q n n n Algorithm A’ wrong ↔ Whole walk in B. Expander: Every set has a large boundary. At every step, it walks outside B w. p. Ω(1). Pr[k steps never out] = 2 Θ(k) Non expander {0, 1}m: all random strings B Boundary

PART II. Quantum Walk

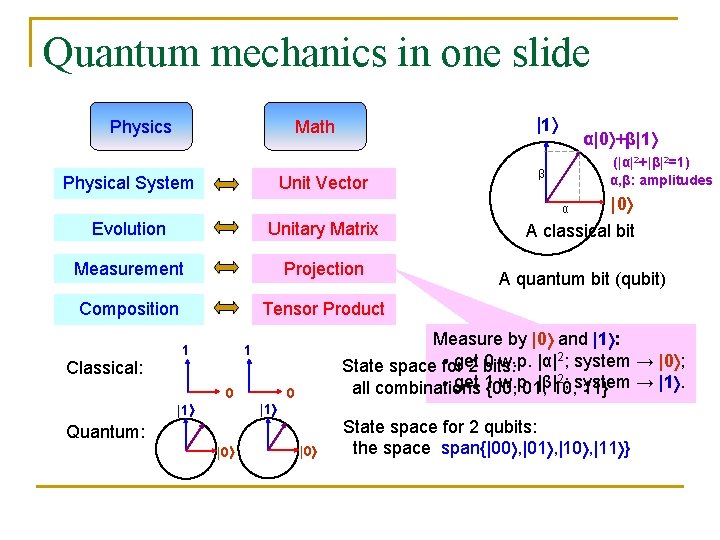
Quantum mechanics in one slide Physics |1 Math Physical System Unit Vector α|0 +β|1 (|α|2+|β|2=1) α, β: amplitudes β α Evolution Unitary Matrix Measurement Projection Composition Tensor Product Classical: 1 0 |1 Quantum: |0 A classical bit A quantum bit (qubit) Measure by |0 and |1 : get 0 w. p. |α|2; system → |0 ; State space for 2 bits: 2; system → |1. get 1{00, w. p. |β|10, all combinations 01, 11} 1 0 |0 State space for 2 qubits: the space span{|00 , |01 , |10 , |11 }

Quantum walk n Many things become quite tricky. n Even the definition of quantum walk. n We’ll ignore the formal definitions here, but only present some results.

Type 1: Discrete Quantum Walk

Coin register n n The most natural quantum counterpart of random walk is the following: each vertex v gives its neighbors (equally) some “mass” so that the l 2 norm of the total mass is still 1. However, simply accumulating all mass from neighbors does not work q n n The operator is not unitary. To overcome this, we need a register to remember where the mass is from. µ ¶ It amounts to add a coin register. 1 1 1 q q Flip the quantum coin: |v |c → |v H|c , where H = Walk accordingly: |v |c → |nc(v) |c , where nc(v) is the cth neighbor of v. p 2 1 ¡ 1

General graph n n Given any random walk on an undirected graph G, Szegedy proposed a method to transform it into a quantum walk Set hitting time: q q n Classical set hitting time = O((ε∆) 1) q ε : density of the target set, i. e. |T|/|V| q n A a target set T⊆ V is hidden in the graph Starting from the uniform distribution, what’s the expected time to hit some point in T? ∆: eigenvalue gap of matrix P [Szegedy] Quantum set hitting time = O(√Classical set hitting time) = O((ε∆) 1/2) V T

Quantum algorithm for Element Distinctness n n Element Distinctness: To decide whether all input integers are distinct. [Ambainis] Discrete quantum walk on the following graph: (r = n 2/3) V = {S⊆[n]: |S| = r}; q q n E = {(S, T): |S∩T| = r 2} Eigenvalue gap: ∆ = 1/r Target set density: ε = r 2/n 2 Quantum running time = setup time + hitting time = O(r) + O((ε∆) 1/2) = O(r + n/√r) = O(n 2/3).

Type 2: Continuous Quantum Walk

Continuous quantum walk on a graph n Given an undirected graph G, and a Hermitian matrix H that respects the graph structure q q n Hermitian: (HT)* = H. Respect G: Hij = 0 if (i, j)∉E. The dynamics ψ(t) = ∑j αi(t)|i for H is governed by the Schrodinger equation i(d/dt) αi(t) = ∑j: (i, j)∊EHijαj(t), which has solution |ψ(t) = ei. Ht |ψ(0).

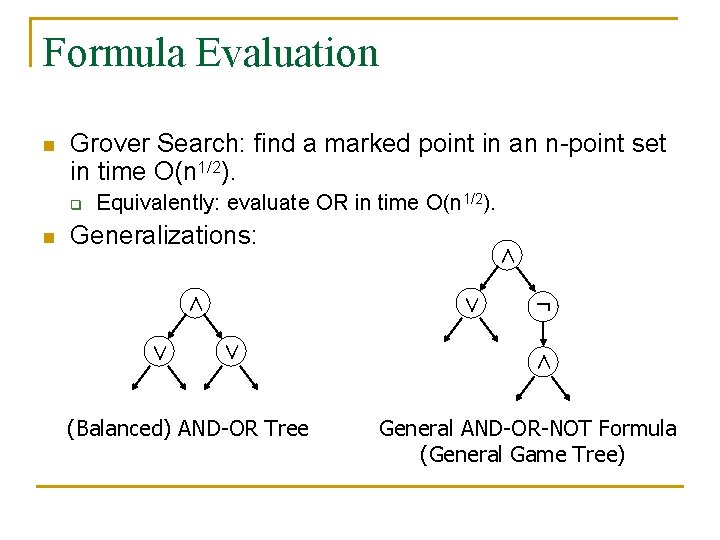
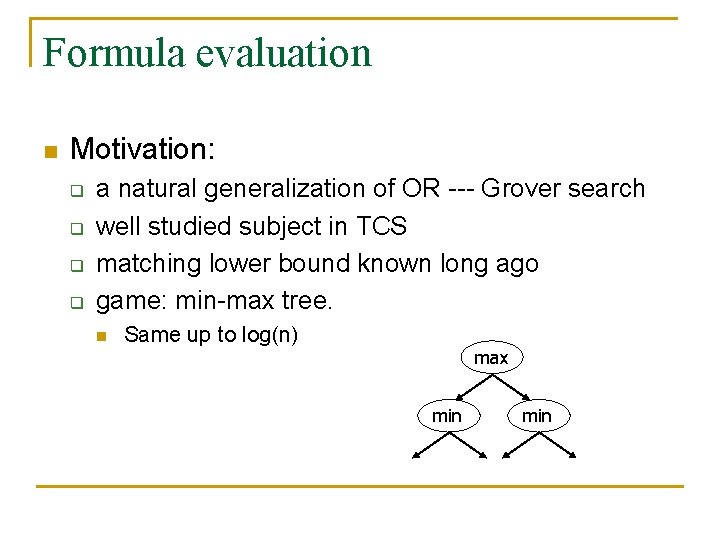
Formula Evaluation n Grover Search: find a marked point in an n point set in time O(n 1/2). q n Equivalently: evaluate OR in time O(n 1/2). Generalizations: ∧ ∨ ∨ (Balanced) AND-OR Tree ¬ ∧ General AND-OR-NOT Formula (General Game Tree)

Formula evaluation n Motivation: q q a natural generalization of OR Grover search well studied subject in TCS matching lower bound known long ago game: min max tree. n Same up to log(n) max min

Breakthroughs n [FGG, 07] An O(n 1/2) algorithm for Balanced AND OR Tree. q q n Method: scattering theory… Not really understandable for computer scientists… [CRSZ, A, FOCS’ 07] An O(n 1/2+o(1)) algorithm for General AND OR NOT Formula. q q q Method: phase estimation + quantum walk. Simpler algorithm, simpler proof. For special cases like Balanced AND OR Tree: O(n 1/2)

Classical implications n n n [OS, STOC’ 03] Any formula f of size n has polynomial threshold function thr(f) = O(n 1/2)? Our result: ~ thr( f ) ≤ deg( f ) ≤ Q( f ) ≤ n 1/2+o(1) [Klivans. Servedio, STOC’ 01; KOS, FOCS’ 02] Definition of thr [BBCMd. W, JACM’ 01] q Class C of Boolean functions has thr(f) ≤ r for all f C, ⇒ C can be learned in time n. O(r) (in both PAC or adversarially generated examples) n n 1/2+o(1) [Implication] Formulas are learnable in time 2 This is very interesting because studies of quantum algorithms solve a purely classical open problem! This is not uncommon in quantum computing!

Sketch of the algorithm n n {AND, OR, NOT}⇔{NAND} For the formula f and an input x, construct a graph Gx x 1: 0 x 2 : 1 x 3: 0 x 4: 1 x 5: 1 n Let A be the adjacency matrix of Gx; consider A’s spectrum.

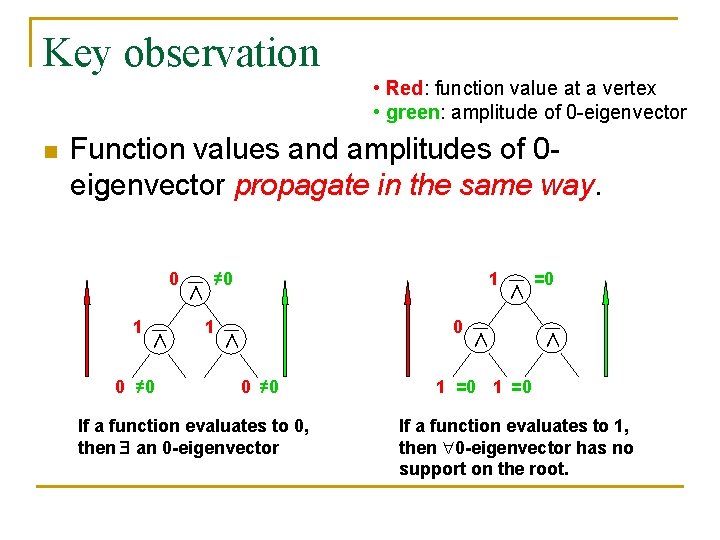
Key observation • Red: function value at a vertex • green: amplitude of 0 eigenvector n Function values and amplitudes of 0 eigenvector propagate in the same way. 0 1 ∧ 0 ≠ 0 ∧ 1 1 0 ∧ 0 ≠ 0 If a function evaluates to 0, then an 0 -eigenvector ∧ ∧ =0 ∧ 1 =0 If a function evaluates to 1, then 0 -eigenvector has no support on the root.

Phase Estimation n n Thus qualitatively, it’s enough to know whethere is a 0 eigenvector with support on root. Phase estimation: Given an unitary operator U (to use) and an eigenvector |ψ , find the phase θ in the corresponding eigenvalue eiθ. q n n Unitary matrix: all eigenvalues have l 2 norm 1 For ei. Ht, the phase is nothing but the corresponding eigenvalue of H. The quantum walk is here! Thus use phase estimation, we can find an eigenvalue of H. q Depending on whether it’s 0, output the answer to f(x).

A highlevel structure of algorithm n We need to carefully choose weight hij on edges (i, j) s. t. the above qualitative connection also works quantitatively. q For f(x) = 0, n q For f(x) = 1, n n an 0 eigenvector with Ω(1) support on root. eigenvector with support on root has eigenvalue Ω(n 1/2) Algorithm: Starting from the root, use quantum walk to carry out the Phase Estimation, output the answer depending on whether the phase is 0.

Summary n n n Random walk is a simple but powerful tool. There will sure be more important algorithmic applications to be found. Theories of quantum walk have been rapidly developed in the past couple of years. A lot of fundamental issues yet to be better understood. Significant breakthrough algorithms using quantum walk are ahead!

Reference n For random walk on graphs: q q n Lovász, Random Walks on Graphs: A Survey, Combinatorics, 353 398, 1996. Chung, Spectral Graph Theory, American Mathematical Society, 1997. For quantum walk: q Quantum computing in general: n n q Textbook by Nielsen and Chuang Lecture notes by Vazirani, by Ambainis, and by Childs Quantum walk: n n Surveys by Kempe and by Santha. All above lectures have nice chapters for quantum walk.

Thanks!