Random Walk and Diffusion Models Convergence of Opinions


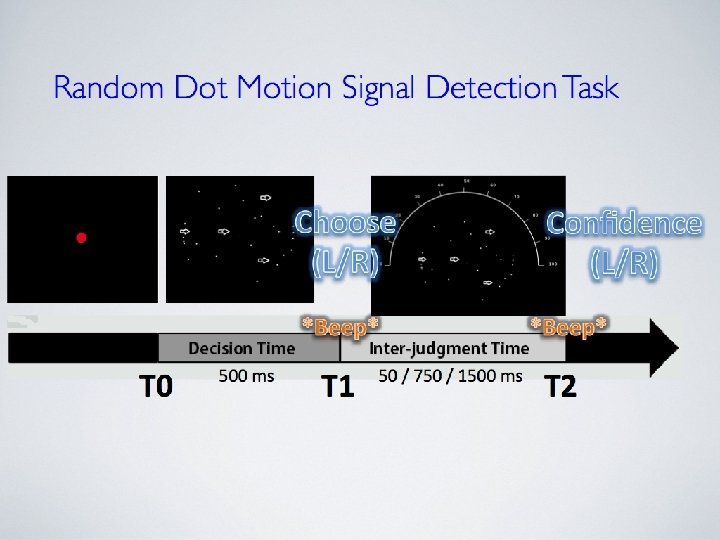












- Slides: 19

Random Walk and Diffusion Models

Convergence of Opinions • Neural Recording – Gold & Shadlen (2002) – Schall (2003) • Sensory Processing – Vickers (1979) – Smith (1995) – Rudd (1996) • Perceptual Discrimination – Laming (1968) – Link & Heath (1975) – Usher & Mc. Clelland (2001) • Memory Recognition – Ratcliff (1978) • Categorization – Nosofsky & Palmeri (1997) – Ashby (2000) • Risky Decision Making – Busemeyer & Townsend (1993) – Diederich (1997)

A Progression of Ideas Diffusion Process Theory Signal Detection Theory Random Walk Theory Neural Network Theory

Origins of Signal Detection Theory • Tanner & Birdsall (Engineers) • Green & Swets (1966)

Basic Ideas of Signal Detection Theory 1. 2. • Take a fixed sample of N observations { X 1 X 2 … XN } Compute the evidence for each hypothesis LS = log ( p[ Hi | {X 1 X 2 … XN }] ) LN = log ( p[ Hi | {X 1 X 2 … XN }] ) LLR = LS – LN Choose Signal if evidence exceeds bias Choose HS if LLR > bias

Two Signal Detection Parameters • d’ = discriminability between the distributions based on strength of evidence • c = response bias based on prior beliefs and payoffs

Explanatory Power of Signal Detection Theory • Choice Probabilities – Hits = Pr( correctly respond signal ) – False Alarms = Pr( falsely respond signal) – Confidence in choice

Origins of Random Walk Theory • Statistics – Wald, De. Groot , Blackwell • Stochastic Processes – Cox & Miller, Feller, • Decision Theory – Ward Edwards, Amnon Rapoport • Psychology – Stone, Laming, Link, Heath, Vickers

Basic Ideas of Random Walk Theory 1. Sequentially Sample Observations over time { X 1 X 2 … Xn. . . } 2. Cumulate the evidence online V(n) = log{p[Xn | HS]} – log{p[Xn | HN]} L(n+1) = L(n) + V(n+1) 3. Decide when to stop and then what to choose Stop and choose HS if Li(n) > Threshold Stop and choose HN if Li(n) > Threshold Otherwise continue sampling

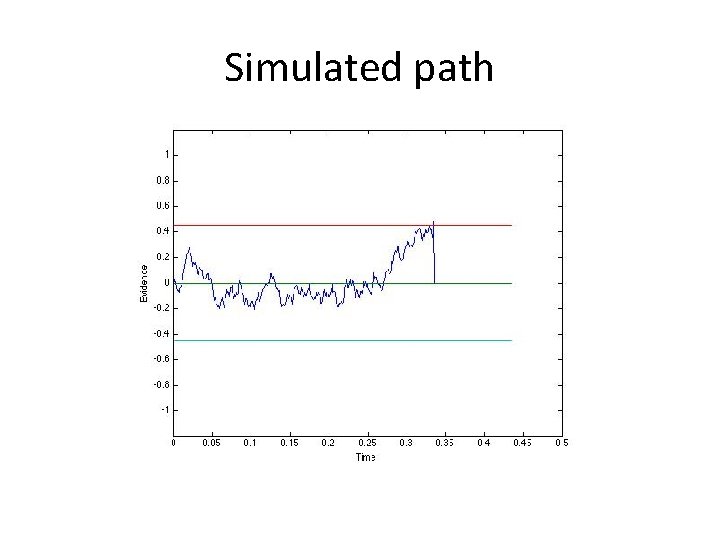
Simulated path

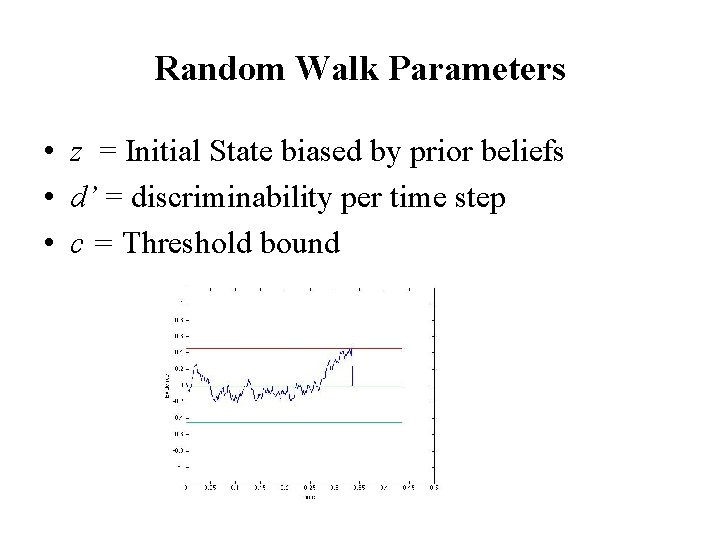
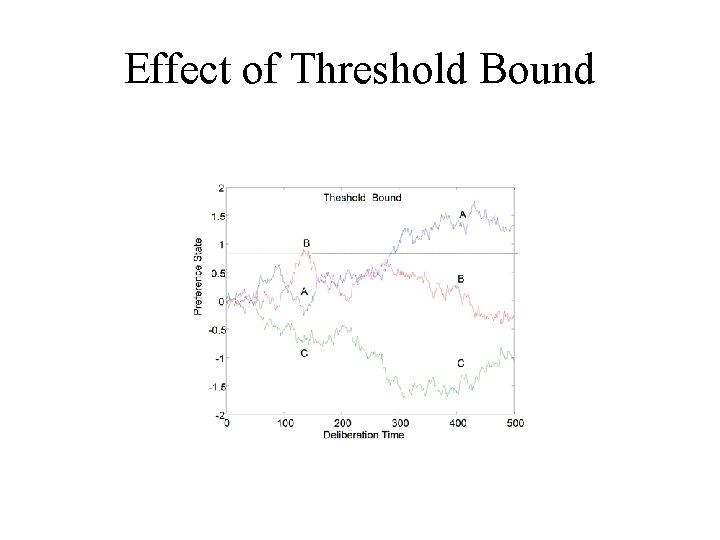
Random Walk Parameters • z = Initial State biased by prior beliefs • d’ = discriminability per time step • c = Threshold bound

Explanatory Power of Random Walk Theories • Choice Probabilities – Hits = Pr( correctly respond signal ) – False Alarms = Pr( falsely respond signal) • Confidence • Speed Accuracy Trade Offs – Changes in hits and false alarms as a function of deliberation time • Mean Response Time – Mean Error Response Time – Mean Correct Response Time

Formulas for Binary Choice For signal trials d = ds > 0 For noise trials d = dn < 0

Origins of Diffusion Models • Physics • Stochastic Process – Karlin & Taylor, Bhattacharya & Waymire • Biology – Tuckwell • Psychology – Ratcliff, Busemeyer, Townsend, Smith, Usher & Mc. Clelland

From Random Walks to Diffusions • Discrete Time Linear System – – – – n = 1, 2, 3, … L(n+1) = (1 -α)L(n) + V(n+1) = random sample of evidence produced by the nth observation V(n+1) = μ + e(n+1) μ = E[ V(n) ] = mean drift rate Var[e(n+1)] = σ2 = variance d’ = (μ / σ) • Approximation to Continuous Time Diffusion – – – t = n∙h 1 h, 2 h, 3 h, …. L(t+h) = (1 -αh) L(t) + V(t+h) = μh + e(t+h)√h μh= E[ V(t) ] = mean drift rate Var[e(t+h)√h] = hσ2 = variance

From Random Walks to Diffusions Continuous time approximation L(t+h) = (1 – αh)∙L(t) + μh + e(t+h)√h = L(t) – αh∙L(t) + μh + e(t+h)√h L(t+h)-L(t) = -αh∙L(t) + μh + e(t+h)√h d. L(t+h) = L(t+h)-L(t) d. L(t+h) = -αh∙L(t) + μh + e(t+h)√h letting h 0 we get Ornstein – Uhlenbeck diffusion model d. L(t) = [μ -α∙L(t) ]dt + e(t)√dt Wiener diffusion model (special case) d. L(t) = μdt + e(t)√dt

Choice and Response Time Distributions for Wiener Process Joint probability density of stopping at time t and responding signal, given start a bias z

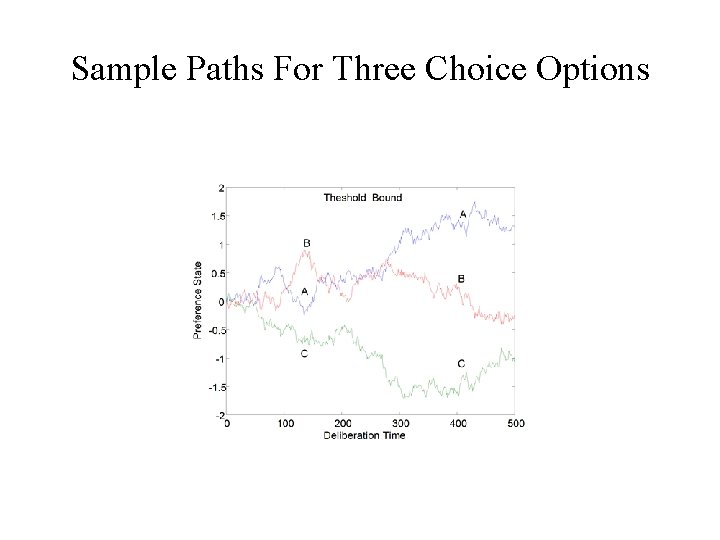
Sample Paths For Three Choice Options

Effect of Threshold Bound