Random Variables Probability Continued Chapter 7 Random Variables

Random Variables Probability Continued Chapter 7

Random Variables Suppose that each of three randomly selected customers purchasing a hot tub at a certain store chooses either an electric (E) or a gas (G) model. Assume that these customers make their choices independently of one another and that 40% of all customers select an electric model. The number among the three customers who purchase an electric hot tub is a random variable. What is the probability distribution?

Random Variable Example X = number of people who purchase electric hot tub X 0 1 2 3 P(X). 216. 432. 288. 064 GGG (. 6)(. 6) EGG GEG GGE (. 4)(. 6)(. 4) EEG GEE EGE (. 4)(. 6)(. 4) EEE (. 4)(. 4)

Random Variables A numerical variable whose value depends on the outcome of a chance experiment is called a random variable. discrete versus continuous

Discrete vs. Continuous The number of desks in a classroom. The fuel efficiency (mpg) of an automobile. The distance that a person throws a baseball. The number of questions asked during a statistics final exam.

Discrete versus Continuous Probability Distributions Which is which? Properties: For every possible x value, 0 < x < 1. l Sum of all possible probabilities add to 1. l Properties: Often represented by a graph or function. l Area of domain is 1. l
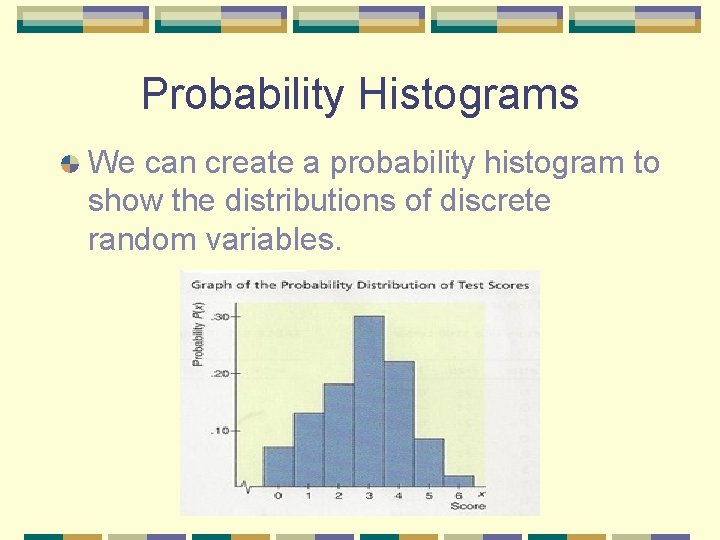
Probability Histograms We can create a probability histogram to show the distributions of discrete random variables.

Example Let X represent the sum of two dice. Then the probability distribution of X is as follows: X 2 3 4 5 6 7 8 9 10 11 12 P(X) 1 36 2 36 3 36 4 36 5 36 6 36 5 36 4 36 3 36 2 36 1 36

Continuous Random Variable and Density Curves The probability distribution of a continuous random variable assigns probabilities under a density curve. Probabilities are assigned to INTERVALS of outcomes rather than to individual outcomes. A probability of 0 is assigned to every individual outcome in a continuous probability distribution.
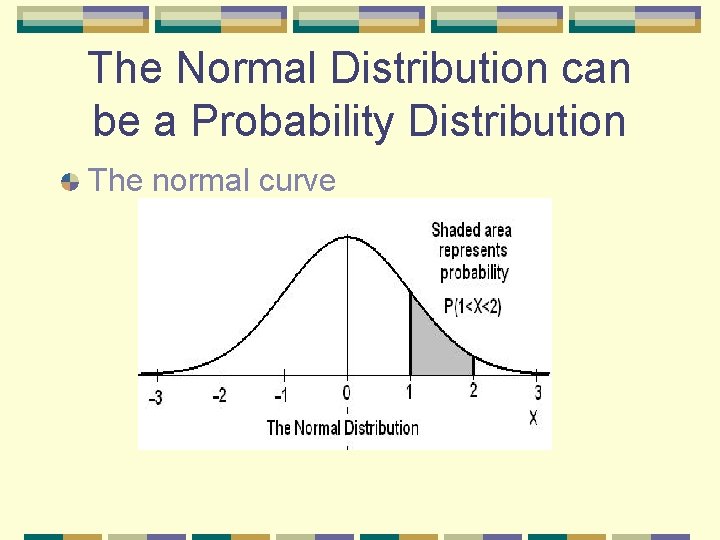
The Normal Distribution can be a Probability Distribution The normal curve

Means and Variances The mean value of a random variable X (written mx ) describes where the probability distribution of X is centered. We often find the mean is not a possible value of X, so it can also be referred to as the “expected value. ” The standard deviation of a random variable X (written sx )describes variability in the probability distribution.

Mean of a Random Variable Example Below is a distribution for number of visits to a dentist in one year. X = # of visits to the dentist. Determine the expected value, variance and standard deviation.

Formulas Mean of a Random Variable Variance of a Random Variable

Mean of a Random Variable Example E(X) = 0(. 1) + 1(. 3) + 2(. 4) + 3(. 15) + 4(. 05) = 1. 75 visits to the dentist

Variance and Standard Deviation of a Random Variable Example Var(X) = (0 – 1. 75)2(. 1) + (1 – 1. 75)2(. 3) + (2 – 1. 75)2(. 4) + (3 – 1. 75)2(. 15) + =. 9875 (4 – 1. 75)2(. 05)
- Slides: 15