Random Variables Lesson 5 2 Analyzing Discrete Random

Random Variables Lesson 5. 2 Analyzing Discrete Random Variables Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Analyzing Discrete Random Variables Learning Targets After this lesson, you should be able to: ü Make a histogram to display the probability distribution of a discrete random variable and describe its shape. ü Calculate and interpret the mean (expected value) of a discrete random variable. ü Calculate and interpret the standard deviation of a discrete random variable. Statistics and Probability with Applications, 3 rd Edition 2
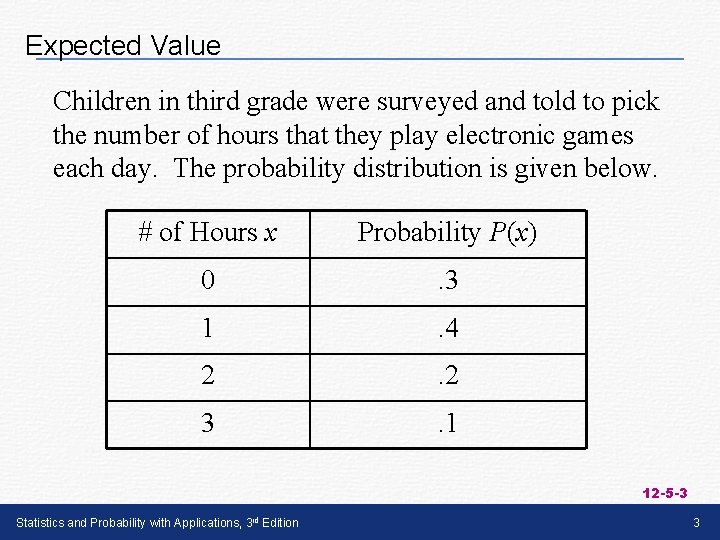
Expected Value Children in third grade were surveyed and told to pick the number of hours that they play electronic games each day. The probability distribution is given below. # of Hours x Probability P(x) 0 . 3 1 . 4 2 . 2 3 . 1 12 -5 -3 Statistics and Probability with Applications, 3 rd Edition 3

Expected Value Compute a “weighted average” by multiplying each possible time value by its probability and then adding the products. 1. 1 hours is the expected value (or the mathematical expectation) of the quantity of time spent playing electronic games. © 2008 Pearson Addison-Wesley. All rights reserved Statistics and Probability with Applications, 3 rd Edition 12 -5 -4 4

Analyzing Discrete Random Variables The mean (expected value) of any discrete random variable is an average of the possible outcomes, but a weighted average in which each outcome is weighted by its probability. Mean (Expected Value) of a Discrete Random Variable The mean (expected value) of a discrete random variable is its long-run average value over many, many repetitions of the same chance process. Suppose that X is a discrete random variable with probability distribution Value x x x … Probability 1 2 3 p 1 p 2 p 3 … To find the mean (expected value) of X, multiply each possible value of X by its probability, then add all the products: Statistics and Probability with Applications, 3 rd Edition 5

Finding and interpreting the mean Define the random variable V to be the number of vehicles in a randomly selected household in the United States. The table below gives the probability distribution for V. Number of vehicles Probability 0 1 2 3 4 0. 0 9 0. 3 4 0. 3 7 0. 1 4 0. 0 6 Calculate and interpret the expected value of V. Statistics and Probability with Applications, 3 rd Edition 6

Example: Finding Expected Winnings A player pays $3 to play the following game: He rolls a die and receives $7 if he tosses a 6 and $1 for anything else. Find the player’s expected net winnings for the game. © 2008 Pearson Addison-Wesley. All rights reserved Statistics and Probability with Applications, 3 rd Edition 12 -5 -7 7

Example: Finding Expected Winnings Solution The information for the game is displayed below. Die Outcome Payoff Net P(x) 1, 2, 3, 4, or 5 $1 –$2 5/6 6 $7 $4 1/6 –$10/6 $4/6 Expected value: E(x) = –$6/6 = –$1. 00 © 2008 Pearson Addison-Wesley. All rights reserved Statistics and Probability with Applications, 3 rd Edition 12 -5 -8 8

Games and Gambling A game in which the expected net winnings are zero is called a fair game. . © 2008 Pearson Addison-Wesley. All rights reserved Statistics and Probability with Applications, 3 rd Edition 12 -5 -9 9

What Is a Fair Game? A fair game is game with expected value zero. So if you play a fair game many times, you would expect, on average, to break even. Statistics and Probability with Applications, 3 rd Edition 10

Example 4 – A Fair Game? Suppose that you play the following game. A card is drawn from a deck. If the card is an ace, you get a payout of $10. If the card is not an ace, you have to pay $1. (a) Is this a fair game? (b) If the game is not fair, find the payout amount that would make this game a fair game. Statistics and Probability with Applications, 3 rd Edition 11

Example 4(a) – Solution In this game you get a payout of $10 if an ace is drawn (probability and you lose $1 if any other card is drawn (probability ). ), So the expected value is Since the expected value is not zero, the game is not fair. If you play this game many times, you would expect to lose, on average, $0. 15, per game. Statistics and Probability with Applications, 3 rd Edition 12

Example 4(b) – Solution We want to find the payout x that makes the expected value 0. cont’d Solving this equation we get x = 12. So a payout of $12 for an ace would make this a fair game. =0 Statistics and Probability with Applications, 3 rd Edition 13

What Is a Fair Game? Games of chance in casinos are never fair; the gambler always has a negative expected value This makes gambling profitable for the casino and unprofitable for the gambler. Statistics and Probability with Applications, 3 rd Edition 14

Analyzing Discrete Random Variables With the mean as our measure of center for a discrete random variable, it shouldn’t surprise you that we’ll use the standard deviation as our measure of spread. Standard Deviation of a Discrete Random Variable The standard deviation of a discrete random variable measures how much the values of the variable typically differ from the mean. Suppose that X is a discrete random variable with probability distribution Value x 1 x 2 x 3 … Probability p 1 p 2 p 3 … and that µX is the mean of X. The standard deviation of X is Statistics and Probability with Applications, 3 rd Edition 15

LESSON APP 5. 2 How much do college grades vary? Indiana University Bloomington posts the grade distributions for its courses online. In a recent semester of a Business Statistics course, 45. 7% of students received A’s, 36. 2% B’s, 13. 8% C’s, 3. 2% D’s, and 1. 1% F’s. Choose a Business Statistics student at random. The student’s grade on a 4 -point scale (with A = 4) is a random variable X with this probability distribution: Value Probability 0 1 2 0. 011 0. 032 0. 138 3 4 0. 362 0. 457 1. Calculate and interpret the mean of X. 2. Calculate and interpret the standard deviation of X. Statistics and Probability with Applications, 3 rd Edition 16

Analyzing Discrete Random Variables Learning Targets After this lesson, you should be able to: ü Make a histogram to display the probability distribution of a discrete random variable and describe its shape. ü Calculate and interpret the mean (expected value) of a discrete random variable. ü Calculate and interpret the standard deviation of a discrete random variable. Statistics and Probability with Applications, 3 rd Edition 17
- Slides: 17